- 2021-06-15 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习利用空间向量求空间角学案(全国通用)
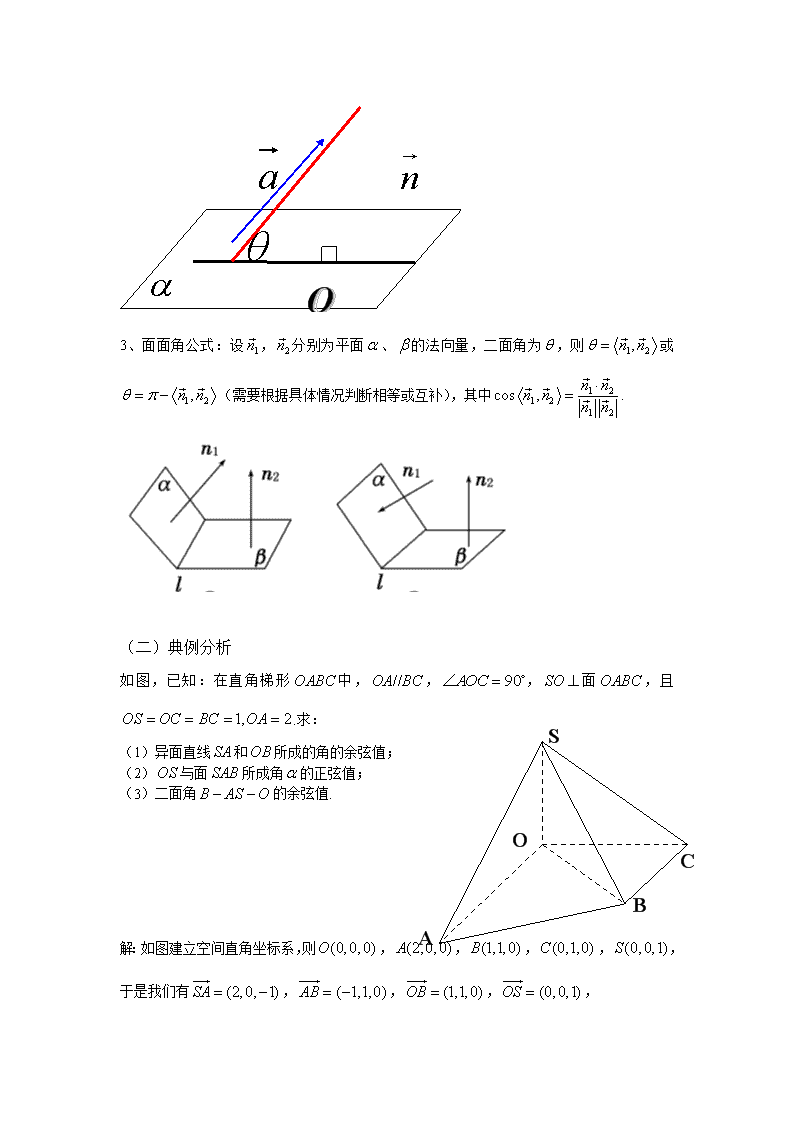
利用空间向量求空间角 一、高考考纲要求: 能用向量方法解决异面直线的夹角、线面角、面面角问题.体会向量法在立体几何中的应用. 二、命题趋势: 在高考中,本部分知识是考查的重点内容之一,主要考查异面直线所成角、线面角、面面角的计算,属中档题,综合性较强,与平行垂直联系较多. 三、教目标 知识与技能:能用向量法熟练解决异面直线的夹角、线面角、面面角的计算问题,了解向量法在研究立体几何问题中的应用; 过程与方法:通过向量这个载体,实现“几何问题代数化”的思想,进一步发展生的空间想象能力和几何直观能力; 情感态度价值观:通过数形结合的思想和方法的应用,进一步让生感受和体会空间直角坐标系,方向向量,法向量的魅力. 四、教重难点 重点:用向量法求空间角——线线角、线面角、二面角; 难点:将立体几何问题转化为向量问题. 五、教过程 (一)空间角公式 1、异面直线所成角公式:如图,设异面直线,的方向向量分别为,,异面直线,所成的角为,则. 2、线面角公式:设直线为平面的斜线,为的方向向量,为平面的法向量,为与所成的角,则. O 3、面面角公式:设,分别为平面、的法向量,二面角为,则或(需要根据具体情况判断相等或互补),其中. (二)典例分析 O A B C S 如图,已知:在直角梯形中,,,面,且.求: (1)异面直线和所成的角的余弦值; (2)与面所成角的正弦值; (3)二面角的余弦值. 解:如图建立空间直角坐标系,则,,,,,于是我们有,,,, (1), 所以异面直线和所成的角的余弦值为. (2)设平面的法向量, 则,即 取,则,,所以, . (3)由(2)知平面的法向量, 又平面,是平面的法向量, 令,则有. ∴二面角的余弦值为. (三)巩固练习 1、在长方体中,,,点、分别,的中点,求: (1)异面直线和所成的角的余弦值;(2)与平面所成角的正弦值; (3)平面与平面所成的锐二面角的余弦值. 解析:以为原点,分别以射线,,,为轴、轴、 轴的非负半轴建立空间直角坐标系,由于,,所以,,,,,,,,则,,,,. (1), ∴异面直线和所成的角余弦值为; (2)设平面的法向量,则有 则,即 令,则,,所以, 又设与平面所成的角为, 则. (3)由(2)知平面的法向量, 又平面,是平面的法向量, 令,则. 故所成的锐二面角的余弦值为. 2、如图所示,四棱锥,为边长为的正三角形,,,垂直于平面于,为的中点,,求: (1)异面直线与所成角的余弦值; (2)平面与平面所成二面角的余弦值. 解:(Ⅰ)如图,以A为坐标原点建立空间直角坐标系A−xy , 因为AD=1,CD=,AC=2, 所以AD⊥CD,∠DAC=, ∴ADBC. ,,,, ,, 则,, ∴, ∴异面直线AB与PC所成角的余弦值为. (Ⅱ)设平面PAB法向量为=(x1,y1, 1), 可得 令,则, 又, 设平面PCD法向量为, 可得 令,则=,则 . ∴平面PAB与平面PCD所成二面角的余弦值为. (四)课堂小结 1.用向量来求空间角,都需将各类角转化成对应向量的夹角来计算,问题的关键在于确定对应线段的向量. 2.合理建立空间直角坐标系 (1)一般来说,如果已知的空间几何体中含有两两垂直且交于一点的三条直线时,就以这三条直线为坐标轴建立空间直角坐标系;如果不存在这样的三条直线,则应尽可能找两条垂直相交的直线,以其为两条坐标轴建立空间直角坐标系,即坐标系建立时以其中的垂直相交直线为基本出发点. (2)建系的基本思想是寻找其中的线线垂直关系,在没有现成的垂直关系时要通过其他已知条件得到垂直关系,在此基础上选择一个合理的位置建立空间直角坐标系. [易错防范 1.利用向量求角,一定要注意将向量夹角转化为各空间角.因为向量夹角与各空间角的定义、范围不同. 2.求二面角要根据图形确定所求角是锐角还是钝角. (五)课后作业 三维设计——课时跟踪检测(四十八)查看更多