- 2021-06-15 发布 |
- 37.5 KB |
- 8页

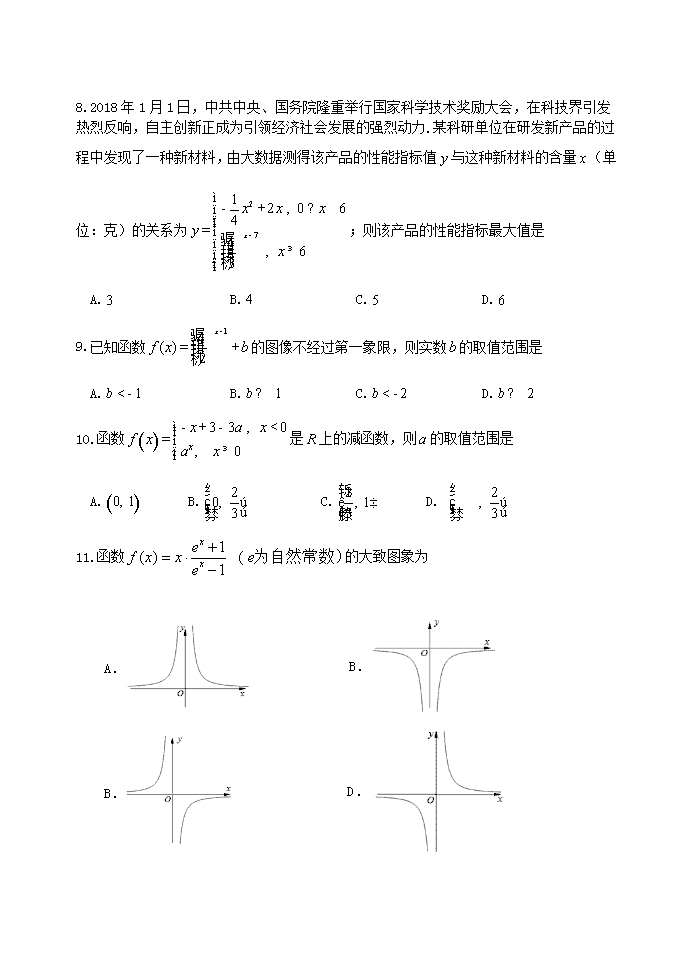

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年福建省永安市第一中学高一上学期第一次月考试题 数学
永安一中 2019—2020学年上学期第一次月考 高一数学试题 (考试时间:120分钟 总分:150分) 第Ⅰ部分(选择题,共60分) 一.选择题(本大题共12小题,每小题5分,共60分。在每小题列出的四个选项中,只有一项是最符合题目要求的.) 1.设集合,,则 A. B. C. D. 2.函数的定义域是 A. B. C. D. 3.下列函数中,为偶函数的是 A. B. C. D. 4.下列各组函数是同一函数的是 ①与; ②与; ③与; ④与 . A.①② B.①④ C.②③ D.②④ 5.设是定义在上的奇函数,当时,,则= A. B. C. D.3 6.若,,,则的大小关系为 A. B. C. D. 7.函数的值域是 A. B. C. D. 8.2018年1月1日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强烈动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值与这种新材料的含量(单位:克)的关系为;则该产品的性能指标最大值是 A. B. C. D. 9.已知函数的图像不经过第一象限,则实数的取值范围是 A. B. C. D. 10.函数是上的减函数,则的取值范围是 A. B. C. D. 11.函数的大致图象为 A. B. B. D. 12.函数是上的奇函数,且在上是增函数,又,则的解集是 A. B. C. D. 第II部分(选择题,共90分) 二.填空题(本大题共4小题,每题5分,共20分.) 13.若,则的值是 ▲ . 14.若函数,则 ▲ . 15.已知函数且则= ▲ . 16.若函数的定义域为,则实数的取值范围是 ▲ . 三.解答题(本大题共6小题,17题10分,其余每题12.) 17.计算:(10分)(1); (2) 18. (12分)已知集合,, (1)求和; (2)若,求实数的取值范围. 19. (12分)已知函数f(x)是定义域为上的奇函数, 当时,且. (1)求函数在上的解析式; (2)作出函数的图象并写出函数的单调 区间. 20. (12分)已知指数函数的图象过点. (1) 求函数的解析式; (2) 设函数,求函数的值域. 21.(12分)已知一次函数是上的减函数,, 且 . (1)求函数的解析式; (2)当时,有最大值,求实数的值. 22.(12分)已知函数有如下性质:如果常数,那么该函数在上是减函数,在上是增函数. (1)用函数单调性定义证明在 上的单调性; (2)设函数,x∈[0,1],利用前面结论求函数f(x)的值域; (3)对于(2)中的函数和函数,若对任意x1∈[0,1],总存在 x2∈[0,1],使得成立,求实数a的取值范围. 永安一中 2019—2020学年上学期第一次月考 高一数学参考答案 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C D C B A D C B D B A A 13. -1 14. 15. 16. 17.解:(1)原式= (5分) (1) 原式 . (10分) 18.解:(1); ; (6分) (2) 当时,;当时, 综上的取值范围是 (12分) 19.解:(1)由f(2)=0得 设,则,, 又f(x)为奇函数,所以,于是时, 所以; (6分) (2)画出函数f(x)的图象,如图(略): 由图可知函数的减区间为; 增区间为和 (12分) 20解:设,因为其图象过点,则,计算得: ,所以. (6分) (1) 依题意可知,由函数为减函数可知: 函数为减函数,当; 又 , 所以的值域为. (12分) 21. 【解】(1)∵是上的减函数,∴设 故 ∴,解得或 又,得 ,∴ (6分) (2) 由(1)知,则对称轴 ①当 即时,解得,符合; ②当时,即时,,得或; 由 故 由①②可得或. (12分) 22.(1)证明:设, , 又由,则,则, 故函数函数在上单调递减; (4分) (2), 设,x∈[0,1],则,则,u∈[1,2]. 由已知性质得, 当,即时,f(x)单调递减;所以减区间为; 当,即时,f(x)单调递增;所以增区间为; ,得f(x)的值域为 (8分) (3)由(2)知f(x)的值域为, 又为减函数,故,x∈[0,1]. 由题意知,f(x)的值域是g(x)的值域的子集, 则有,解可得, 故a的取值范围是. (12分)查看更多