- 2021-06-15 发布 |
- 37.5 KB |
- 6页


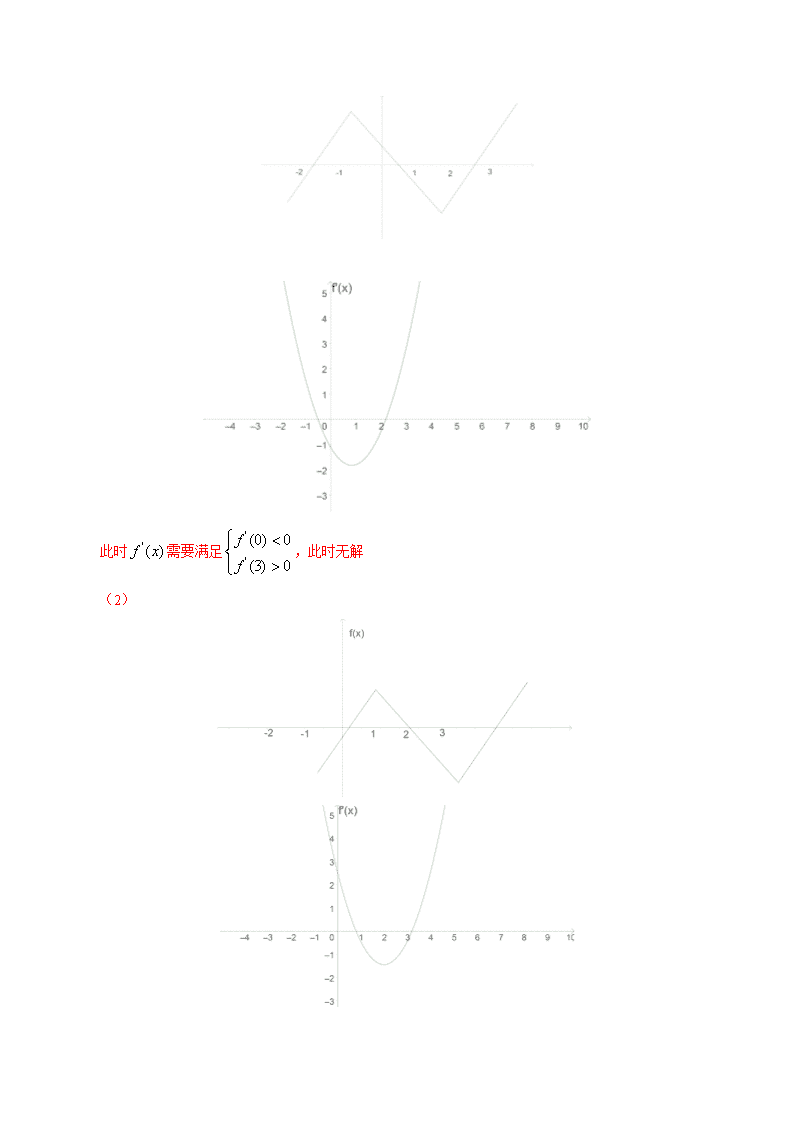
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习求参数范围问题学案(全国通用)
专题04 求参数范围问题 一、与单调性有关的参数问题 此时参数可以位于函数中也可以位于区间内,常见的提问方式是函数在某个区间单调递减、单调递增、单调、不单调,研究这类问题的关键是把握原函数和导函数的关系,这里需要注意的一个问题:若函数单调,则恒为非正或非负,函数的极值点并不等同于导函数的零点,极值点的个数和导函数的根的个数也不能直接划等号。 例1.已知函数在区间上单调递减,求的取值范围。 【解析】先根据函数单调性作出函数的趋势图像,再安排存在参数的区间位置即可。学 令,则或;令,则,作出趋势图像如下: 函数在区间上单调递减,需满足 例2.已知函数在上是减函数,求实数的取值范围。 【解析】转化为函数单调性与导函数的正负性的关系即可, 在上是减函数,即在上恒成立 令,因为在上递减,则 所以 例3.已知函数,若函数在区间上为单调函数,求的取值范围。 【解析】题目只是说明函数是单调函数,并未说明是单增还是单减,因此需要分两种情况讨论,将单调性 转化为参数恒成立问题即可。 , 例4.已知函数,其中,若函数在区间上不是单调函数,求的取值范围。 【解析】这个问题相对复杂些,但是思路还算清晰,函数在上不是单调函数,意味着原函数在上 存在极值点,因为三次函数极值点的个数可能是两个也可能没有,原题目中排出没有的情况,因此题目存 在两个极值点,但是这两个极值点有几个落在区间内这是个问题,可能只有一个极值点在,也可能两 个都在,此外极值点是导函数的根,题目即可转化为二次函数在区间内根的分布问题。 ,函数在区间上不是单调函数,则在内必定存在极值 点,此时不能单调递增,只能是保持一种增减增的状态,因此在内的极值点可能是一个也 可能是两个。 若极值点在内只有一个,情况如下: (1) 此时需要满足,此时无解 (2) . 此时只需要满足 若极值点在内有两个,图如下:学- 此时只需要满足 综上所述, 二、与极值有关的参数范围问题 常见的问法是函数有无极值点,有几个极值点的问题,极值点是函数单调性发生改变的点,因此有极值点意味着函数不单调,没有极值点则意味着函数单调,有几个极值点意味着导函数有几个零点,但是导函数有几个零点不等同于函数有几个极值点。 (导函数为零的点不一定为极值点,极值点一定为导函数为零的点) 例5.已知函数,设在上有极值,求的取值范围。 【解析】,,在 上有极值,则在上有零点,即在有根 ,故 例 6.若函数没有极值点,求的取值范围。 【解析】,令,即 函数无极值点,则 例7.已知函数,函数的图像在处的切线的斜率为,且在区间 上不是单调函数,求的取值范围。 【解析】由已知得,,,函数在区间上 . 不是单调函数,则导函数在区间上存在零点,根据二次函数根的分布列不等式 学 三、与双参数有关的参数问题 在参数问题中参数的个数可能不止一个,另外在此类问题中变量的个数也可能不止一个,也可能会出现双变量的问题。 题目中若含有双参数,其中一个一般是给出了区间,而让求另一个未给出的参数的取值范围,除了这个之外一般还会给出未知量的区间,一个参数一个未知量是以任意性和存在性方式给出,其实这种题目大多是参数恒成立或存在性问题的延伸,只不过需要求两次最值,因为多了一个参数,所以在难度上会适当的降低。 解题的思路是将所求的参数单独分离,另一边包括另外一个参数和变量,此时可以将参数或变量中的一个当成自变量,另外一个当做常量即可,求出最值后可消去参数或自变量,再将问题转化为常规恒成立问题即可,但是如果所求的参数不能分离,可分离的是另一个参数,这样反而简单,直接利用任意性或存在性消去参数。 例8.已知函数,若函数的图像在点处的切线 的倾斜角为,对于任意的,函数在区间上总不是单调函数,求的取值范围。 【解析】由题意知, 在区间上总不是单调函数,即在上存在零点 ,根据二次函数根的分布列不等式 ,对于,不等式在上恒成立,则 因为在上单调递减,及,故 综上所述, 例9.设函数,当时,若不等式对所有的都成立,求实数的取值范围。学+ 查看更多