- 2021-06-15 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省常州高级中学2018-2019学年高一上学期期中考试数学试卷
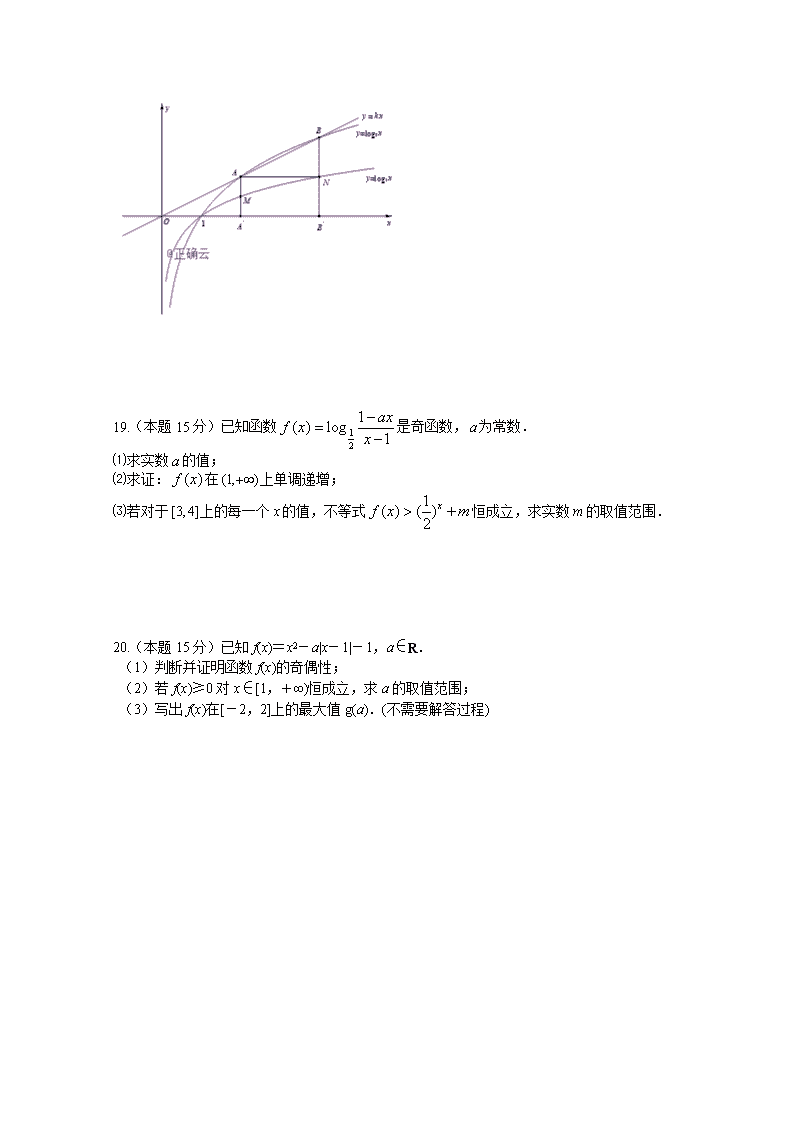
www.ks5u.com 一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应的位置上. 1.设集合,,则= . 2.不等式的解为 . 3.函数的定义域为_________________. 4. 函数的值域为 . 5.已知幂函数的图象过点,则_________. 6.若,,则用“>”将按从大到小可排列为__________. 7.设函数,则__________. 8.已知方程的解所在区间为,则= . 9.若函数 ( 且)的值域是,则实数的取值范围是___________. 10.已知函数,满足对任意的实数()均有 则实数的取值范围是____________. 11.定义在R上的奇函数满足:①在内单调递增,②,则不等式的解为___________. 12.已知函数,设,则的取值范围是___________________. 13.已知函数(为自然对数的底数),且对任意的实数均有不等式恒成立,则实数的取值集合是_________________. 14.已知函数,其中,若的图像上有且只有一对点关于轴对称,则实数的取值范围是________________. 二、解答题:本大题共6小题,共计80分.请在答题纸指定区域内作答,解答应写出文字说明,证明过程或演算步骤. 15.(本题12分)设全集R,集合,. (1)求CU; (2)若集合,满足,求实数的取值范围. 16.(本题12分)求值: (1); (2); (3)函数, 求满足=2的的值. 17.(本题12分)已知函数的定义域为. ⑴求;⑵当时,求的最小值. 18.(本题14分)如图,已知函数的图象与函数的图象交于、两点.过、分别作轴的垂线,垂足分别为、,并且、分别交函数的图象于、两点. ⑴探究线段与的大小关系; ⑵若平行于轴,求四边形的面积. 19.(本题15分)已知函数是奇函数,为常数. ⑴求实数的值; ⑵求证:在上单调递增; ⑶若对于上的每一个的值,不等式恒成立,求实数的取值范围. 20.(本题15分)已知f(x)=x2-a|x-1|-1,a∈R. (1)判断并证明函数f(x)的奇偶性; (2)若f(x)≥0对x∈[1,+∞)恒成立,求a的取值范围; (3)写出f(x)在[-2,2]上的最大值g(a).(不需要解答过程) 一、 填空题:本大题共4小题,每小题5分,共20分. 1.若关于的不等式的解为一切实数,则实数的取值范围是________. 2.设函数是R上的偶函数,且时函数单调递减,则使得成立的的取值范围是___________. 3.若函数在区间上有两个零点,则实数的取值范围是_____________. 4.是R上的偶函数,且当时,,若关于的方程()恰有10个不同的实数解,则的范围是_______. 二、解答题:本题共1小题,总分10分. 5. 已知.(1) 若函数是奇函数,求的表达式; (2)若,,当时,恒有不大于零,求实数的取值范围. 2018—2019年高一数学上学期一卷答案 1. 2. 3. 4. (0,1) 5. 9 6. 7. 9 8. 4 9. 10. 11. 12. 13. 14. 15. 解:(1)∵ ∴ ∴ ……………………………6分 (2)由得 根据数轴可得, 从而 ………………………………12分 16. 解:(1)12 ……………………4分 (2) ……………………8分 (3)设,则,得…………10分 从而, 解得. …………12分 17. 解:⑴要使函数有意义,必须,解得. 故函数的定义域.………………2分 ⑵令,由得,即. 则. ①当即时,(此时); ②当即时,(此时). ③当即时,(此时)9分(每个3分) 综上所述.………………10分 18. 解:⑴.证明如下: 设、,则、. ∴, 又,故.………………6分 ⑵∵平行于轴,∴. 又,,∴联立方程组,解之得. ∴、、、. 故四边形的面积为.………………14分 19. 解:⑴由已知条件得对定义域中的均成立. ∴. 即 ∴对定义域中的均成立. ∴ 即(不合题意,舍去)或.∴ .…………5分 ⑵证明:由⑴知或. 设,则. 又, ∵,∴,,. ∴,从而. 根据对数函数的性质得,即. 故在上单调递增.…………10分 ⑶解:由知,即. 令,则易得在是增函数, ∴.∴要使不等式恒成立,必须. 故的取值范围是.…………15分 20. 解:(1)当a=0时,f(x)=x2-1,f(x)为偶函数, 任意x∈R,f(-x)=(-x)2-1=x2-1=f(x),所以f(x)为偶函数. 当时,所以非奇非偶. …4分 (2)当x∈[1,+∞)时,f(x)=x2-a(x-1)-1=(x-1)(x+1-a) . x=1时,由f(x)≥0成立,得a∈R; x>1时,由f(x)≥0恒成立,得(x-1)(x+1-a)≥0恒成立, 即x+1-a≥0恒成立,所以a≤x+1对x>1恒成立, 所以a≤2. 综上,a的取值范围是(-∞,2].…………8分 (3)f(x)=x2-a|x-1|-1= 因为函数f(x)=x2-ax+a-1在[1,2]上的最大值=max{f(1),f(2)}; f(x)=x2+ax-a-1在[-2,1]上的最大值=max{f(1),f(-2)} . 所以g(a)=max{ f(-2),f(1),f(2)}=max{3-3a,0,3-a} =…………15分 附加卷答案 1. 2. 3. 4. 5. 2 解:(1)函数定义域为,由f(x)是奇函数有, 又,, ,再检验(略). ………4分 (2)当,时, (如右图) 的增区间为、,减区间为 当即时,由图象可知,,即,, 又, 当即时,由图象可知,,即, 同时有,即, 又,适合题意。 综上所述,.………10分查看更多