- 2021-06-15 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年贵州省都匀第一中学高一上学期期中考试数学试题
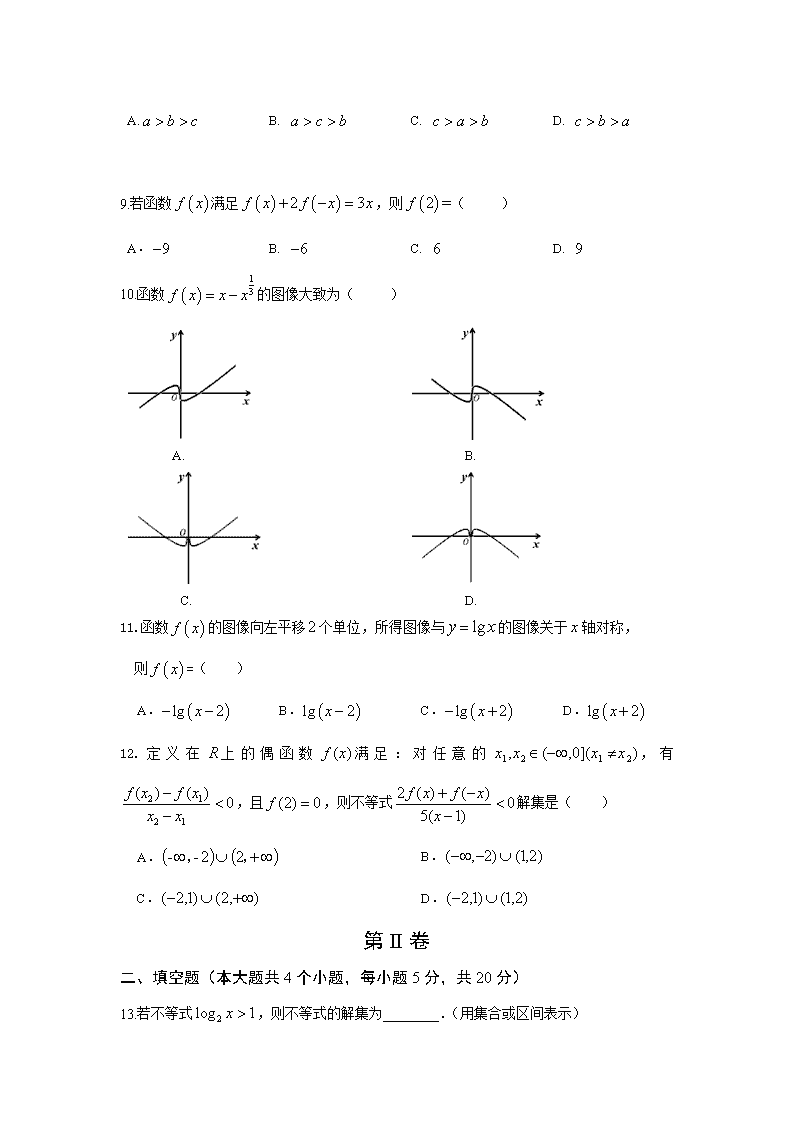
都匀一中2019—2020学年度第一学期 高一年级半期考试数学 本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,第I卷第1页至第2页,第II卷第2页至第4页,考试结束后,请将答题卡交回。满分150分,考试用时120分钟. 第I卷 一、选择题(本大题共12小题,每小题5分,共60分) 1.集合,,则=( ) A. B. C. D. 2.函数的定义域是( ) A. B. C. D. 3.下列函数为幂函数的是( ) A. B. C. D. 4.若指数函数在上是增函数, 则实数的取值范围是( ) A. B. C. D. 5.已知,那么的值为( ). A. B. C. D. 6.下列函数中既是偶函数,又在上是单调递增函数的是( ) A. B. C. D. 7.下列函数中与函数相等的函数是( ) A. B. C. D. 8.,则的大小关系是( ) A. B. C. D. 9.若函数满足,则( ) A. B. C. D. 10.函数的图像大致为( ) A. B. C. D. 11.函数的图像向左平移个单位,所得图像与的图像关于轴对称, 则=( ) A. B. C. D. 12.定义在上的偶函数满足:对任意的,有,且,则不等式解集是( ) A. B. C. D. 第II卷 二、填空题(本大题共4个小题,每小题5分,共20分) 13.若不等式,则不等式的解集为________.(用集合或区间表示) 14.已知函数(且)的图像恒过定点,点的坐标为________. 15.若,则________. 16.若函数有四个零点,则的取值范围为________. 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分10分)计算下列各式的值: (1); (2). 18.(本小题满分12分)已知集合,,且.求实数的取值范围. 19. (本小题满分12分) 某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量(毫克)与时间(小时)之间的关系近似满足如图所示的曲线. (1)写出服药后与之间的函数关系式; (2)进一步测定:每毫升血液中的含药量不少于毫克时,药物对治疗疾病有效.求服药一次治疗疾病的有效时间. 20. (本小题满分12分) 设,.(其中为常数) (1)若为奇函数,求的值; (2)若不等式恒成立,求实数的取值范围. 21.(本小题满分12分) 已知函数为偶函数,且. (1)求的值,并确定的解析式; (2)若(且),求在上的值域. 22. (本小题满分12分) 已知函数的值满足(当时),对任意实数,都有,且,,当时,. (1)求的值,判断的奇偶性并证明; (2)判断在上的单调性,并给出证明; (3)若且,求的取值范围. 都匀一中2019—2020学年度第一学期 高一年级半期考试数学答案 第I卷 一、选择题(本大题共12小题,每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C D A C C B D B B A A B 第II卷 二、填空题(本大题共4个小题,每小题5分,共20分) 题号 13 14 15 16 答案 1 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17.解:(1)原式===·······································5分 (2)原式===······························10分 18.解:∵B⊆A, ①当B=∅时,m+1≤2m-1,解得m≥2;··································5分 ②当B≠∅时,有,解得 ·····················11分 综上所述:··············································12分19.解:(1)当t∈[0,1]时,设函数的解析式为y=kt,将M(1,4)代入,得k=4,∴ y=4t. 又当t∈(1,+∞)时,设函数的解析式为y=, 将点(3,1)代入得a=3,∴ y=. 综上,y=f(t)=··········································8分 (2)由f(t)≥0.25,解得≤t≤5. 所以服药一次治疗疾病的有效时间为5-=(小时).·····················12分 20.解:(1)因为x∈R,所以f(0)=0得a=1. ····································5分 (2)f(x)=a-, 因为f(x)+a0恒成立, 即2a恒成立. 因为2x+1>1,所以0<<2, 所以2a≥2,即a≥1. 故a的取值范围是[1,+∞).············································12分 21.解:(1)因为f(3)查看更多