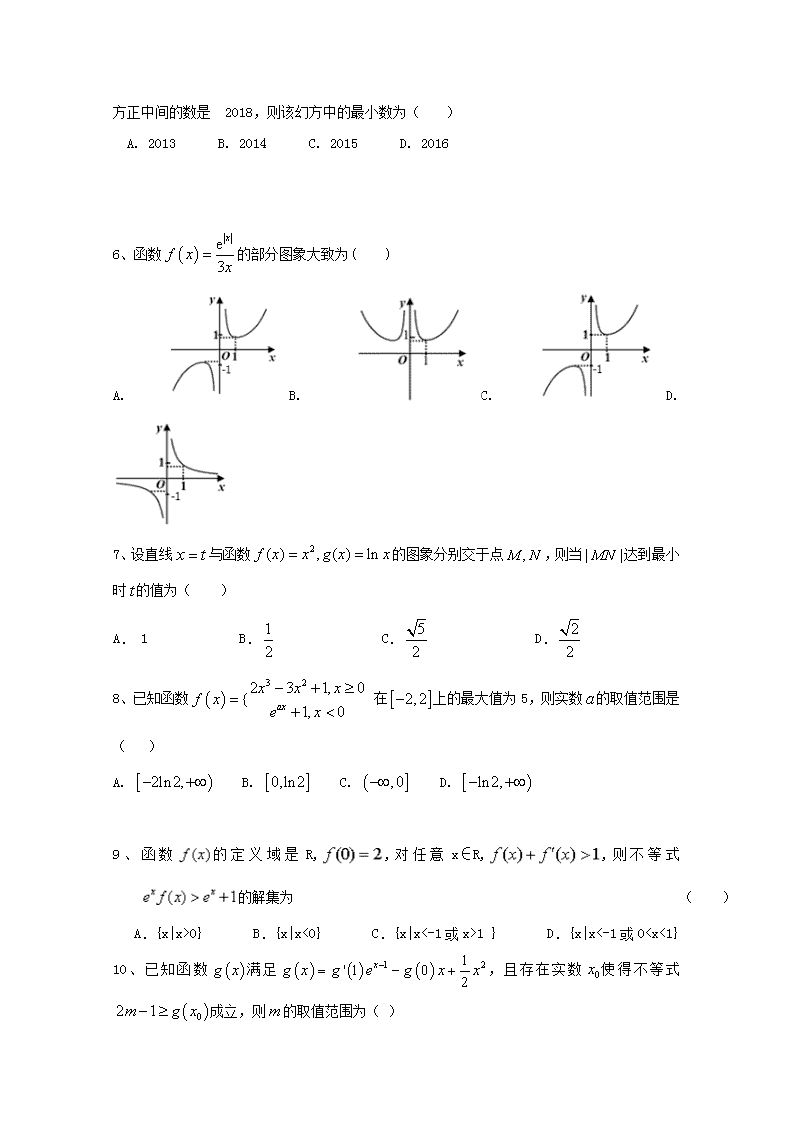2018-2019学年黑龙江省大庆第一中学高二下学期第二次阶段考试数学(理)试题 Word版
大庆一中2018-2019学年高二年级下学期第二次阶段考试数学理试题
一、选择题(12×5=60)
1、已知积分,则实数k=( )
A. 2 B. C. 1 D.
2、已知某物体的运动方程是s=+t,则当t=3s时的瞬时速度是( )
A. B. C. D.
3、P为椭圆上异于左右顶点A1、A2的任意一点,则直线PA1与PA2的斜率之积为定值.将这个结论类比到双曲线,得出的结论为:P为双曲线上异于左右顶点A1、A2的任意一点,则( )
A. 直线与的斜率之和为定值 B. 直线与的斜率之和为定值2
C. 直线与的斜率之积为定值 D. 直线与的斜率之积为定值2
4、设函数在上可导,其导函数为,且函数的图象如图所示,则下列结论中一定成立的是( )
A.函数有极大值和极小值
B.函数有极大值和极小值
C.函数有极大值和极小值
D.函数有极大值和极小值
5、幻方,是中国古代一种填数游戏.n(n∈N*,n≥3)阶幻方是指将连续 n2个正整数排成的正 方形数阵,使之同一行、同一列和同一对角线上的 n 个数的和都相等.中国古籍《周易本义》中的《洛书》记载了一个三阶幻方(如图 1),即现在的图 2.若某3
阶幻方正中间的数是 2018,则该幻方中的最小数为( )
A. 2013 B. 2014 C. 2015 D. 2016
6、函数的部分图象大致为( )
A. B. C. D.
7、设直线与函数的图象分别交于点,则当达到最小时的值为( )
A. 1 B. C. D.
8、已知函数在上的最大值为5,则实数的取值范围是( )
A. B. C. D.
9、函数的定义域是R,,对任意x∈R,,则不等式的解集为 ( )
A.{x|x>0} B.{x|x<0} C.{x|x<-1或x>1 } D.{x|x<-1或0
0,则a的取值范围是( )
A. B. C. D.
12、对于任意的实数,总存在三个不同的实数,使得成立,则实数的取值范围是( )
A. B. C. D.
二、填空题(4×5=20)
13、已知函数(x∈R)上任一点处的切线斜率则该函数的单调递增区间为_____________
14计算定积分 =________________
15、已知函数f(x)与f′(x)的图象如图所示,则函数g(x)=的递减区间为__________.
16、若函数有两个极值点,其中,且,则方程的实根个数为 .
三、解答题(合理写出解题步骤)
17、已知二次函数的图像与直线 相切于点,
(1)求函数 的解析式;
(2)求由的图像、直线及直线所围成的封闭区域的面积.
18、已知函数.
(1)求曲线在点处的切线的方程.
(2)若直线为曲线的切线,且经过坐标原点,求直线的方程及切点坐标.
19、某礼品店要制作一批长方体包装盒,材料是边长为的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是的正方形,然后在余下两个角处各切去一个长、宽分别为、的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
(1)求包装盒的容积关于的函数表达式,并求函数的定义域;
(2)当为多少时,包装盒的容积最大?最大容积是多少?
20、已知函数.
(Ⅰ)求函数在区间上的最小值;
(Ⅱ)证明:对任意,都有成立.
21、已知函数,
(1)求函数的单调区间;
(2)若关于的方程有实数解,求实数的取值范围.
22、已知函数
(1) 当时,求函数的最值;
(2) 求函数的单调区间;
(3) 试说明是否存在实数使的图象与无公共点
二阶段数学考试答案
A C C D B / D D D A A / C D
13【答案】14. 答案 15答案.(0,1),(4,+∞) 16. 答案 5
17解:(1)由得,
因为二次函数的图像与直线 相切于点,
所以,即,解得,
因此.
(2)作函数的图像、直线及直线的图象如下:
则由的图像、直线及直线所围成的封闭区域的面积为;
.
18解析:(1).2
所以在点处的切线的斜率,
∴切线的方程为;4
(2)设切点为,则直线的斜率为,
所以直线的方程为:,6
所以又直线过点0=,
∴,
整理,得,∴,8
∴,的斜率,10
∴直线的方程为,切点坐标为.12
19解析:(1)因为包装盒高,底面矩形的长为,宽为,
所以铁皮箱的体积.
函数的定义域为.
(2)由(1)得,,
令,解得.
当时,,函数单调递增;
当时,,函数单调递减.
所以函数在处取得极大值,这个极大值就是函数的最大值.
又.
答:切去的正方形边长时,包装盒的容积最大,最大容积是.
20【答案】(Ⅰ)由,可得.
当单调递减,
当单调递增.
所以函数在区间上单调递增,
又,
所以函数在区间上的最小值为.
(Ⅱ)由(Ⅰ)可知在时取得最小值,
又,
可知.
由,可得.
所以当单调递增,
当单调递减.
所以函数在时取得最大值,
又,
可知,
所以对任意,都有成立.
21解:(1)函数的定义域为且关于坐标原点对称
为偶函数
当时,
令
令
所以可知:当时,单调递减,
当时,单调递增,
又因为是偶函数,所以在对称区间上单调性相反,所以可得:
当时,单调递增,
当时,单调递减,
综上可得:的递增区间是:,;
的递减区间是: ,
(2)由,即,显然,
可得:令,当时,
显然,当时,,单调递减,
当时,,单调递增,
时,
又,所以可得为奇函数,所以图像关于坐标原点对称
所以可得:当时,
∴的值域为 ∴的取值范围是
22(1) 函数f(x)= x2-ax-aln(x-1)(a∈R)的定义域是(1,+∞)
当a=1时,,所以f (x)在为减函数
在为增函数,所以函数f (x)的最小值为=
(2)
若a≤0时,则f(x)在(1,+∞)恒成立,所以f(x)的增区间为(1,
+∞).
若a>0,则故当,,
当时,f(x) ,
所以a>0时f(x)的减区间为,f(x)的增区间为.
(3) a≥1时,由(1)知f(x)在(1,+∞)的最小值为,
令在 [1,+∞)上单调递减,
所以则>0,
因此存在实数a(a≥1)使f(x)的最小值大于,
故存在实数a(a≥1)使y=f(x)的图象与无公共点