数学（文）卷·2018届辽宁省沈阳市东北育才学校高二下学期第二阶段测试（2017-07）

数学（文）卷·2018届辽宁省沈阳市东北育才学校高二下学期第二阶段测试（2017-07）

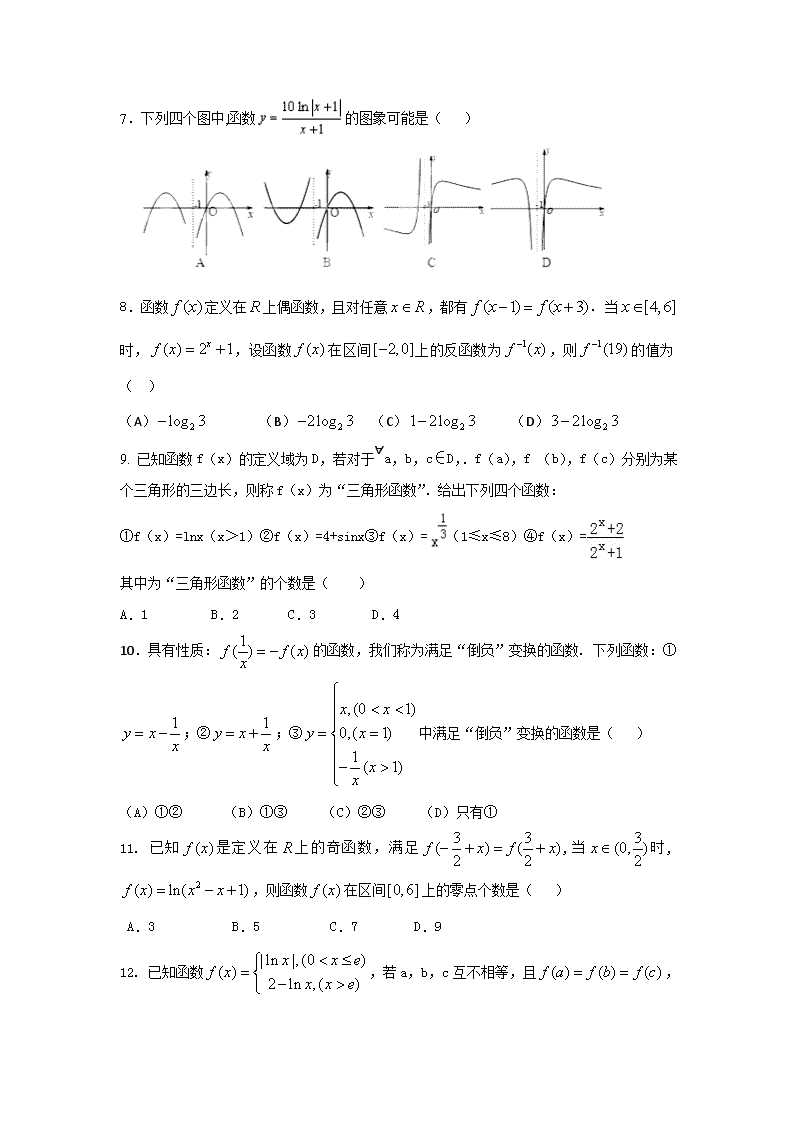
‎2016-2017学年度下学期高二第二次阶段测试 数学（文科）试卷 答题时间：120分钟 满分：150分 命题人：高二备课组 第Ⅰ卷（选择题，共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1. 已知集合A={﹣1，0，1，2}，B={1，x，x2﹣x}，且B⊆A，则x=（　　）‎ A．1 B．‎0 ‎C．2 D．﹣1‎ ‎2. 复数（为虚数单位）的虚部是（　　）‎ ‎ A． B． C． D．‎ ‎3. 已知集合A={x∈R|＜2x＜8}，B={x∈R|﹣1＜x＜m+1}，若x∈B成立的一个充分不必要条件是x∈A，则实数m的取值范围是（　　）‎ A．m≥2 B．m≤‎2 ‎C．m＞2 D．﹣2＜m＜2‎ ‎4. 已知函数 ，若对任意的，不等式恒成立，则实数的取值范围是（ ）‎ ‎ ‎ ‎5. 下列说法正确的是（ ） ‎ A．命题的否定是.‎ B．命题 “已知若则或”是真命题 .‎ C．“在上恒成立”在上恒成立”.‎ D．命题“若，则函数只有一个零点”的逆命题为真命题.‎ ‎6．若函数的图像与函数的图像关于直线对称，则=（ ）‎ ‎ A． B． C． D．‎ ‎7．下列四个图中,函数的图象可能是（ ） ‎ ‎8．函数定义在上偶函数，且对任意，都有. 当时，，设函数在区间上的反函数为，则的值为（ ） ‎ ‎（A） （B） （C） （D）‎ ‎9. 已知函数f（x）的定义域为D，若对于∀a，b，c∈D，．f（a），f （b），f（c）分别为某个三角形的三边长，则称f（x）为“三角形函数”．给出下列四个函数：‎ ‎①f（x）=lnx（x＞1）②f（x）=4+sinx③f（x）=（1≤x≤8）④f（x）=‎ 其中为“三角形函数”的个数是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎10．具有性质：的函数，我们称为满足“倒负”变换的函数. 下列函数：①；②；③中满足“倒负”变换的函数是（ ）‎ ‎（A）①② （B）①③ （C）②③ （D）只有①‎ ‎11. 已知是定义在上的奇函数，满足,当时,，则函数在区间上的零点个数是（ ）‎ ‎ A．3 B．‎5 C．7 D．9‎ ‎12. 已知函数，若a，b，c互不相等，且 ‎，则的取值范围为（ ）‎ A． B． C． D．‎ 第Ⅱ卷（非选择题，共90分）‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13. 直线(t为参数)的倾斜角是 .‎ ‎14. .以下是对命题“若两个正实数满足，则”的证明过程：‎ 证明：构造函数，因为对一切实数，恒有，所以，从而得，所以．‎ 根据上述证明方法，若个正实数满足时，你能得到的结论为 ‎ .（不必证明）‎ ‎15. 已知函数f（x）=，g（x）=kx+1，若方程f（x）﹣g（x）=0有两个不同实根，则实数k的取值范围为　　　　　　．‎ ‎16. 已知：函数对于任意有，且当时，，则以下命题正确的是：‎ ‎①函数是周期为2的偶函数；②函数在上单调递增；③函数的最大值是4；④若关于的方程有实根，则实数m的范围是；⑤当时，。[]‎ 其中真命题的序号是 ‎ 三、解答题（本大题共6小题， 解答应写出文字说明、证明过程或演算步骤）‎ ‎17.（本小题满分10分）‎ 已知关于的不等式．‎ ‎（1）当时，求此不等式的解集；‎ ‎（2）若此不等式的解集为，求实数的取值范围． ‎ ‎18. (本小题满分l2分)‎ 在中学生综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评．某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：‎ 表1：男生 表2：女生 等级 优秀 合格 尚待改进 等级 优秀 合格 尚待改进 频数 ‎15‎ x ‎5‎ 频数 ‎15‎ ‎3‎ y ‎（1）从表二的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率；‎ ‎（2）由表中统计数据填写2×2列联表（在答题纸上），并判断是否有90%的把握认为“测评结果优秀与性别有关”．（参考公式：K2=，其中n=a+b+c+d．）‎ 临界值表：‎ P（K2＞k0）‎ ‎0.1‎ ‎0.05‎ ‎0.01‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎19.(本小题满分l2分)‎ 已知命题关于实数的方程的一根比1大另一根比1小；命题函数在区间上有零点．‎ ‎（1）命题真，假，求实数的取值范围．‎ ‎（2）当命题为真时，实数的取值集合为集合，若命题：为真，则求实数的取值范围．‎ ‎20．(本小题满分l2分) ‎ 在直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为．‎ ‎（1）求的参数方程；‎ ‎（2）若点在曲线上，求的最大值和最小值．‎ ‎21.(本小题满分l2分) 已知函数f（x）= x2 , g（x）=x—1,‎ ‎(1)若存在实数x，使f（x）< b• g（x）,求实数b的取值范围；‎ ‎（2）设F（x）= f（x）—m• g（x）+1—m—m2, 且 | F（x）| 在【0,1】上单调递增，求实数m的取值范围.‎ ‎22．(本小题满分l2分) 已知函数f（x）=2x +k•2﹣x（x∈R）．‎ ‎（1）判断函数f（x）的奇偶性，并说明理由；‎ ‎（2）设k＞0，问函数f（x）的图象是否关于某直线x=m成轴对称图形，如果是，求出m的值；如果不是，请说明理由；（可利用真命题：“函数g（x）的图象关于某直线x=m成轴对称图形”的充要条件为“函数g（m+x）是偶函数”）‎ ‎（3）设k=﹣1，函数h（x）=a•2x﹣21﹣x﹣a，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．‎