数学文卷·2018届广东省清远市高二上学期期末教学质量检测（2017-01）

数学文卷·2018届广东省清远市高二上学期期末教学质量检测（2017-01）

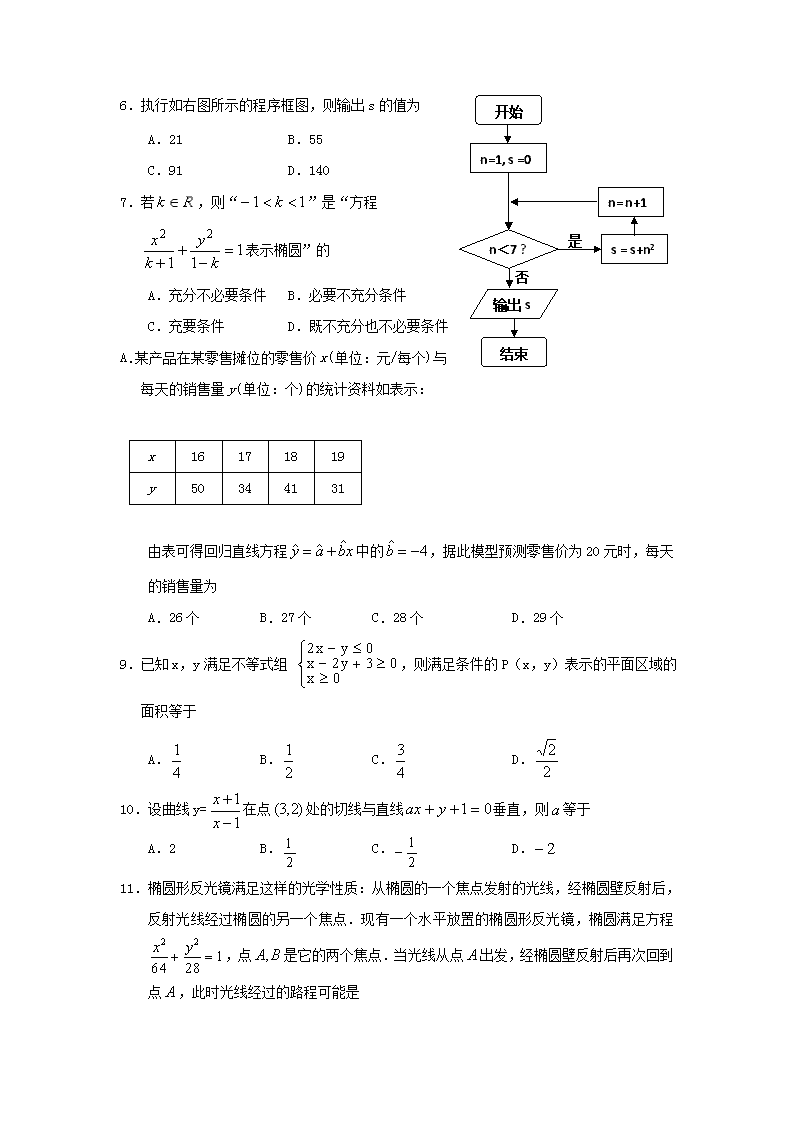
广东省清远市2016—2017学年度第一学期期末教学质量检测 高二文科数学试卷 本试卷共4页，共22小题，满分150分,考试用时120分钟。‎ 参考公式：1．锥体的体积公式v=其中S为锥体的底面积，h为锥体的高。‎ ‎ 2．用最小二乘法求回归方程的系数计算公式：‎ 第一卷（选择题，共60分）‎ 一、 选择题（本大题共12小题，每小题5分,共60分。每小题只有一个选项是符合题目要求的，请把正确答案的代号填入答题卡中。）‎ ‎1．已知集合M={x| (x+2)(x-3) ≤0}，N={﹣3，﹣1，1，3，5}，则M∩N=‎ ‎ A．{1，3} B．{﹣3，﹣1，1} C．{﹣3，1} D．{﹣1，1，3}‎ ‎2．下列四个命题中真命题为 ‎ A． B． C．若，则 D．若，则 ‎3．一个总体中有100个个体，随机编号为0，1，2，3，…，99，依编号顺序平均分成10个小组，组号依次为1，2，3，…10．现用系统抽样方法抽取一个容量为10的样本，若第1组随机抽取的号码为m=6，则在第7组中抽取的号码是 ‎ A．66 B．76 C．63 D．73‎ ‎4．如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图，根据茎叶图计算数据的中位数为 ‎ A．98 B．94 C．94.5 D．95 ‎ B C D E A ‎5．如图，四边形为距形,，以为圆心，为半径画圆，交线段于，在圆弧上任取一点，则直线与线段有公共点的概率为 ‎ A． B． C． D．‎ n=1, s =0‎ n﹤7 ?‎ s = s+n2‎ n= n+1‎ 输出s 结束 开始 是 否 ‎6．执行如右图所示的程序框图，则输出s的值为 ‎ A．21 B．55 ‎ ‎ C．91 D．140‎ ‎7．若，则“”是“方程表示椭圆”的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ ‎ C．充要条件 D．既不充分也不必要条件 A． 某产品在某零售摊位的零售价x(单位：元/每个)与每天的销售量y(单位：个)的统计资料如表示： ‎ ‎ ‎ x ‎16‎ ‎17‎ ‎18‎ ‎19‎ y ‎50‎ ‎34‎ ‎41‎ ‎31‎ ‎ 由表可得回归直线方程中的，据此模型预测零售价为20元时，每天的销售量为 ‎ A．26个 B．27个 C．28个 D．29个 ‎9．已知x，y满足不等式组 ，则满足条件的P（x，y）表示的平面区域的面积等于 A． B． C． D．‎ ‎10．设曲线y=在点处的切线与直线垂直，则等于 ‎ ‎ A．2 B． C． D． ‎ ‎11．椭圆形反光镜满足这样的光学性质：从椭圆的一个焦点发射的光线，经椭圆壁反射后，反射光线经过椭圆的另一个焦点．现有一个水平放置的椭圆形反光镜，椭圆满足方程，点是它的两个焦点．当光线从点出发，经椭圆壁反射后再次回到点，此时光线经过的路程可能是 ‎ A．32或4或 B．或28或 ‎ ‎ C．28或4或 D．32或28或4‎ 二、 对于三次函数，给出定义：设是函数的导数，是的导数，若方程=0有实数解，则称点为函数的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数，则 =‎ ‎ A．100 B．99 C．50 D．0‎ 第二卷（非选择题，共90分）‎ 13. 填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡的横线上）‎ (1) 命题“若，则”的逆否命题是 （3分）；并判定原命题是真命题还是假命题？__________（2分）.‎ ‎14．抛物线C：的焦点F坐标是___________.‎ ‎15．函数的单调增区间是___________.‎ ‎16．规定记号“”表示一种运算，即ab＝＋a＋b (a，b为正实数)．若1k＝3，则k的值为_______（2分），此时函数f(x)＝的最小值为_______（3分）．‎ 三、解答题（本大题共6小题，共70分。解答应写出文字说明、演算步骤或证明过程）‎ ‎17．(本小题满分10分)某公司的管理者通过公司近年来科研费用支出（百万元）与公司所获得利润（百万元）的散点图发现，与之间具有线性相关关系，具体数据如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 科研费用（百万元）‎ ‎1.6‎ ‎1.7‎ ‎1.8‎ ‎1.9‎ ‎2.0‎ 公司所获利润y（百万元）‎ ‎1‎ ‎1.5‎ ‎2‎ ‎2.5‎ ‎3‎ ‎（1）求对的回归直线方程；（参考数据：=16.3，=18.5）‎ ‎（2）若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元，预测2017年该公司可获得的利润为多少万元？‎ ‎18．（本小题满分12分）‎ ‎2016年“五一节”期间，高速公路车辆较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：‎ ‎ （1）求a的值，并说明交警部门采用的是什么抽样方法？‎ ‎ （2）求这120辆车行驶速度的众数和平均数的估计值（精确到0.1）；‎ ‎ （3）若该路段的车速达到或超过90km/h即视为超速行驶，试根据样本估计该路段车辆超速行驶的概率.‎ 19． ‎（本小题满分12分）‎ 某营养师要求为某个学生预定午餐和晚餐，已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位碳水化合物，6个单位的蛋白质和10个单位的维生素C. 另外，该学生这两餐需要的营养中至少含64个单位的单位碳水化合物，42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐，晚餐的费用分别为2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该学生每天分别预定多少个单位的午餐和晚餐？‎ 20． ‎（本小题满分12分）‎ 已知命题p:方程表示的曲线是焦点在x轴的双曲线；命题q：关于的不等式成立.‎ ‎（1）若=，且为真，求实数m的取值范围.‎ ‎（2）若p是q的充分不必要条件，求实数a的取值范围.‎ ‎21．（本小题满分12分）已知椭圆C: ()的离心率 ‎，原点到过点，的直线的距离是.‎ ‎ （1）求椭圆的方程； ‎ ‎ （2）是否存在直线 （）交椭圆于不同的两点，且都在以为圆心的圆上，若存在，求出的范围；若不存在，请说明理由.‎ ‎22．（本小题满分12分）已知函数．‎ ‎ （1）当时，讨论函数的单调性；‎ ‎ （2）若对任意m，n∈（0，2）且m≠n，有恒成立，求实数的取值范围．‎ 清远市2016—2017学年度第一学期期末教学质量检测 高二文科数学参考答案 一、 选择题：（本大题共12小题，每小题5分,共60分）‎ 序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D A A C D C B D C D D B 13. 填空题: （本大题共4小题，每小题5分，共20分）‎ ‎13. 若，则 （3分）， 假 （2分）； 14． （0,1）；‎ 15. ‎（0，+∞）；或填写 [0，+∞）；（不写区间的不得分） ‎ 16. ‎ 1 （2分）， 3 （3分）；（注意：答得2分）‎ 三、解答题 ‎17（本小题满分10分）‎ 解：（1）经计算可得 ‎ ， ，，…………4分 b== …………6分 a=－b=2－5=-7. …………7分 故所求的回归直线方程为=5x-7. …………8分 ‎(3)由题可知到2017年时科研投入为（百万元），故可预测该公司所获得的利润为（百万元）。…………9分 答：可预测2017年该公司获得的利润为450万元 …………10分 ‎18解：（Ⅰ）由图知：‎ ‎，....2分 ‎ ∴，...............3分 车速 Km/h ‎ 该抽样方法是系统抽样； ...........4分 (2)众数是最高矩形底边中点的横坐标，‎ ‎∴众数的估计值为： = ；......6分 平均数的估计值为： ‎ ‎ ‎ ‎(3)估计该路段车辆超速的概率 ‎19. （本小题满分12分） ‎ 解：设为该学生每天分别预订x个单位的午餐和y个单位的晚餐，费用为Z，.......1 分 ‎ 设则Z=2.5x+4y .............2分 由题意知约束条件为：------------------------6分 画出可行域如下图：‎ ‎...........................8 分 变换目标函数： ...........................9 分 当目标函数过点A，即直线6x+6y=42与6x+10y=54的交点（4，3）时，F取得最小值．...........................11 分 ‎ 即要满足营养要求，并且花费最少，应当为该学生分别预订4个单位的午餐和3个单位的晚餐． ----------------12分 ‎20.（本小题满分12分） ‎ 解： （1）方法一： ∵为真 ∴p真且q真 ……………1分 P真：则设A={m|}=，…………………2分 ‎ q真：B={m|}=…………………3分 ‎∵ ∴B= …………………4分 ‎∴‎ ‎∴实数m的取值范围为: …………………6分 方法二：∵为真 ∴p真且q真 …………1分 P真：则设A={m|}=，…………………2分 q真：∵ ∴………………3分 ‎ ∴B= …………………4分 ‎∴‎ ‎∴实数m的取值范围为: …………………6分 ‎(2) 由（1）知设A={m|}，B=……………8分 ‎∵p是q的充分不必要条件， ∴A是B的真子集 ‎ ‎∴…………………10分 解得，…………………11分 ‎∴实数a的取值范围为：. …………………12分 ‎ 21.（本小题满分12分）‎ ‎ 解：（1），...............1分 原点到直线AB:的距离...................2分 ‎ ............................................3分 所求的椭圆方程： ..................................4分 ‎（2） 消y整理得：...6分 B A C D E 设，,的中点是 ，‎ 则，..................7分 ‎. .....................8分 所以即，‎ 即，‎ ‎ （）........................9分 又即，......10分 ‎ . ...............................11分 综上所述，不存在这样的直线，交椭圆于不同的两点，且这两点都在以为圆心的圆上。‎ ‎ ..............................12 分 ‎22．（本小题满分12分）‎ ‎【解答】解：（1）函数的定义域为（0，+∞），‎ ‎（2）若m＞n，由得f（m）﹣m＜f（n）﹣n 若m＜n，由得f（m）﹣m＞f（n）﹣n 令，所以g（x）在（0，2）上单调递减…..............5分 又..............6分 ‎（1）当a=0时，g′（x）=0，不符合题意；..............7分 ‎（2）当a＞0时，由g′（x）＜0得0＜x＜2a，..............8分 所以g（x）在（0，2a）上递减，‎ 所以2≤2a，即a≥1 ..............9分 ‎（3）当a＜0时，在（0，+∞）上，都有g′（x）＜0..............10分 所以g（x）在（0，+∞）上递减，即在（0，2）上也单调递减..............11分 综上，实数a的取值范围为（-∞，0）∪ [1，+∞）..............12分