数学文卷·2017届四川省遂宁市射洪中学高三“三诊”模拟考试（2017

数学文卷·2017届四川省遂宁市射洪中学高三“三诊”模拟考试（2017

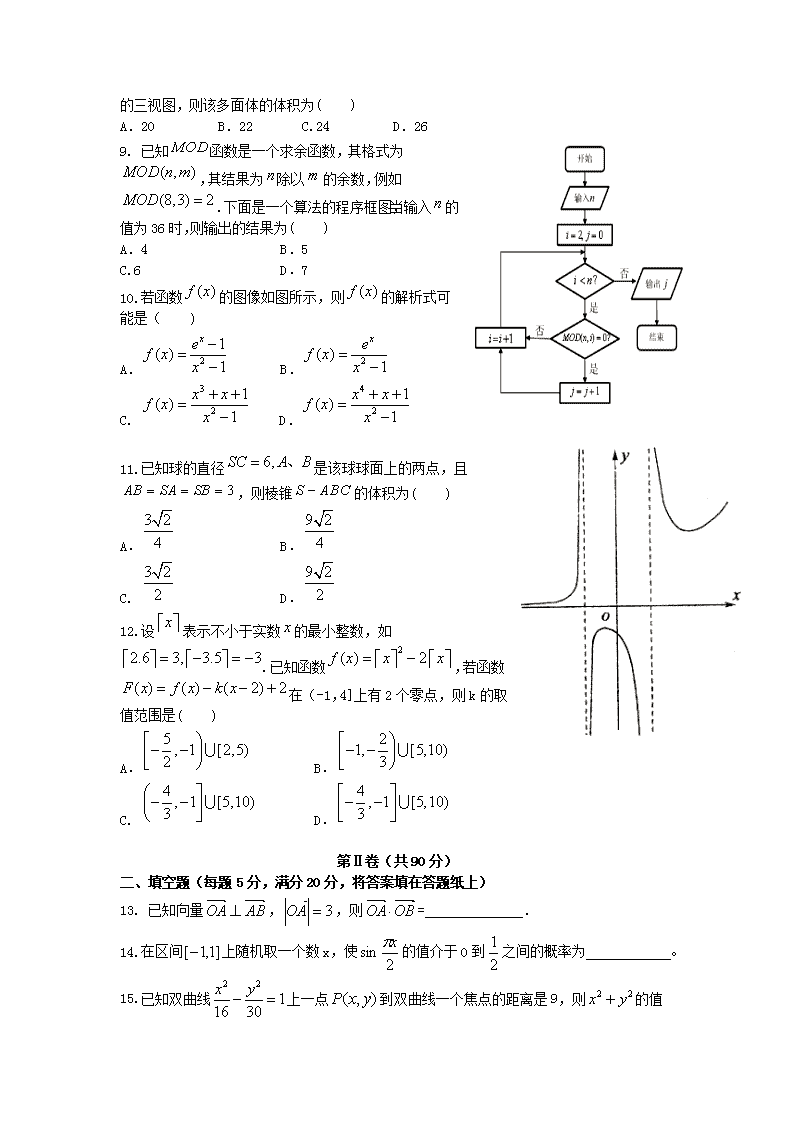
‎】射洪中学高2014级“三诊”模拟考试 数学试题（文科）‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若，则=( )‎ A． B.1 C．5 D．25‎ ‎2. 设集合，，则 ( )‎ A.{1,2} B．{-1,-2} ‎ C．{-2,-1,2} D．{-2,-1,0,2}‎ ‎3. 向量满足，则向量与的夹角为（ ）‎ A. 45° B. 60° C. 90° D. 120°‎ ‎4.已知一组数据的线性回归方程为，则的值为（ ）‎ A. 2 B. 4 C. -4 D. -2‎ ‎5.已知，则（ ）‎ A. B. ‎ C. D. ‎ ‎6.在△ABC中，，BC边上的高等于，则（ ）‎ A. B. ‎ C. D. ‎ ‎7.《九章算术》是我国古代的数字名著，书中《均输章》有如下问题：“今有五人分五钱，令上二人所得与下三人等.问各得几何.”其意思为“已知五人分5钱，两人所得与三人所得相同，且每人所得依次成等差数列.问五人各得多少钱？”（“钱”是古代的一种重量单位）.在这个问题中，所得为( )‎ A．钱 B．钱 C. 钱 D. 钱 ‎8.如图，网格纸上小正方形的边长为1‎ ‎，实线画出的是某多面体的三视图，则该多面体的体积为( )‎ A．20 B．22 C.24 D．26‎ ‎9. 已知函数是一个求余函数，其格式为，其结果为除以的余数，例如.下面是一个算法的程序框图，当输入的值为36时，则输出的结果为( )‎ A．4 B．5 ‎ C.6 D．7‎ ‎10.若函数的图像如图所示，则的解析式可能是（ )‎ A． B． ‎ C. D．‎ ‎11.已知球的直径是该球球面上的两点，且，则棱锥的体积为( )‎ A． B． ‎ C. D．‎ ‎12.设表示不小于实数的最小整数，如.已知函数，若函数在（-1，4]上有2个零点，则k的取值范围是( )‎ A． B． ‎ C. D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 已知向量，，则= ．‎ ‎14.在区间上随机取一个数x，使的值介于0到之间的概率为 。‎ ‎15.已知双曲线上一点到双曲线一个焦点的距离是9，则 的值是 ．‎ ‎16.将函数的函数图像向右平移个单位以后得到的图像与的图像关于对称，则的最小正值是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本小题满分12分）‎ 已知数列的前n项和满足。‎ ‎（1）求证：数列为等比数列；‎ ‎（2）设函数求。‎ ‎18、（本小题满分12分）‎ 射洪某中学共有学生2000名，各年级男、女生人数如下表：‎ 初一年级 初二年级 初三年级 女生 ‎373‎ x y 男生 ‎377‎ ‎370‎ z 已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.‎ （1） 求x的值；‎ （2） 现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？‎ （3） 已知y245,z245,求初三年级中女生比男生多的概率.‎ ‎19、（本小题满分12分）‎ 已知四棱台ABCD—A1B1C1D1的上、下底面分别是边长为2和4的正方形，AA1=4且AA1⊥底面ABCD，点P为DD1的中点。‎ ‎(1)求证：AB1⊥平面PBC；‎ ‎(2)在BC边上找一点Q，使PQ//平面A1ABB1，并求三棱锥Q—PBB1的体积。‎ ‎20. （本小题满分12分）‎ 设椭圆的左、右焦点分别为,上顶点为，过与垂直的直线交轴负半轴于点，且为的中点.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）过的直线与C交于不同的两点、，则的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由.‎ ‎21. （本小题满分12分）‎ 已知函数，‎ ‎（1）求函数的最大值； ‎ ‎（2）当时，讨论函数与函数的图象的交点个数.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22、在直角坐标系xOy中，曲线C1的参数方程为（其中为参数），曲线C2：，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系。‎ ‎（1）求曲线C1的普通方程和曲线C2的极坐标方程；‎ ‎（2）若射线与曲线C1，C2分别交于A，B两点，求。‎ ‎23.选修4-5：不等式选讲 已知关于的方程在上有解.‎ ‎（Ⅰ）求正实数取值所组成的集合；‎ ‎（Ⅱ）若对任意恒成立，求实数的取值范围.‎ 射洪中学高2014级“三诊”模拟考试 数学试题（文科）参考答案 1. B ‎ 2. C ‎ 3. C 4. D 5. A 6. D ‎7. A 设 ‎ ‎8. C 27个小立方体取走3个 ‎9. D 10.B 11.D ‎12. C 作出图像，由数形结合可知：C满足题意 ‎13. 9‎ ‎14. ‎ ‎15.133 不妨设点P在右支上（可排除点在左支上的情况），由条件可知P点到右焦点距离为9，‎ ‎ 解出 ‎16. ‎ ‎,‎ ‎17.‎ ‎18、解：（1） ‎ ‎ （2）初三年级人数为y＋z＝2000－373＋377＋380＋370）＝500，‎ ‎ 现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为： 名 ‎ （3）设初三年级女生比男生多的事件为A ，初三年级女生男生数记为（y，z）；‎ ‎ 由（2）知 ，且 ,基本事件空间包含的基本事件有：‎ ‎（245，255）、（246，254）、（247，253）、……（255，245）共11个 事件A包含的基本事件有：‎ ‎（251，249）、（252，248）、（253，247）、(254,246)、(255,245) 共5个 ‎ ‎ ‎19、‎ ‎ ‎ ‎20、【解析】（1）由题，为的中点.设，则，‎ ‎，，由题，即，‎ ‎∴即，‎ 故所求的椭圆的方程为.‎ ‎（2）设，，由题异号，‎ 设的内切圆的半径为，则的周长为，‎ ‎，‎ 因此要使内切圆的面积最大，只需最大，此时也最大，‎ ‎，‎ 由题知，直线的斜率不为零，可设直线的方程为，‎ 由得，‎ 由韦达定理得，，（）‎ ‎，‎ 令，则，，‎ 当时，有最大值3，此时，，，‎ 故的内切圆的面积的最大值为，此时直线的方程为.‎ ‎21、【解析】（1），由，列表如下：‎ ‎1‎ ‎+‎ ‎0‎ ‎-‎ 单调递增 极大值1‎ 单调递减 因此增区间，减区间，极大值，无极小值.故函数的最大值为 ‎ ‎(2)令，问题等价于求函数的零点个数．‎ ‎①当时，有唯一零点；当时，.‎ ‎②当时，,当且仅当时取等号，所以为减函数．注意到,所以在内有唯一零点；‎ ‎③当时，当，或时，时，，所以在和上单调递减，在上单调递增．‎ 注意到，‎ 所以在内有唯一零点；‎ ‎④当时，，或时，时，，‎ 所以在和上单调递减，在上单调递增．‎ 注意到，‎ 所以在内有唯一零点. ‎ 综上，有唯一零点，即函数与的图象有且仅有一个交点.‎ ‎22、‎ ‎ ‎ ‎23. 当 时..........2分 ‎.......6分 ‎ .......10分 ‎（若其他解法正确，可酌情赋分）‎