2019-2020学年湖南省湘南中学高一入学考试数学试题

2019-2020学年湖南省湘南中学高一入学考试数学试题

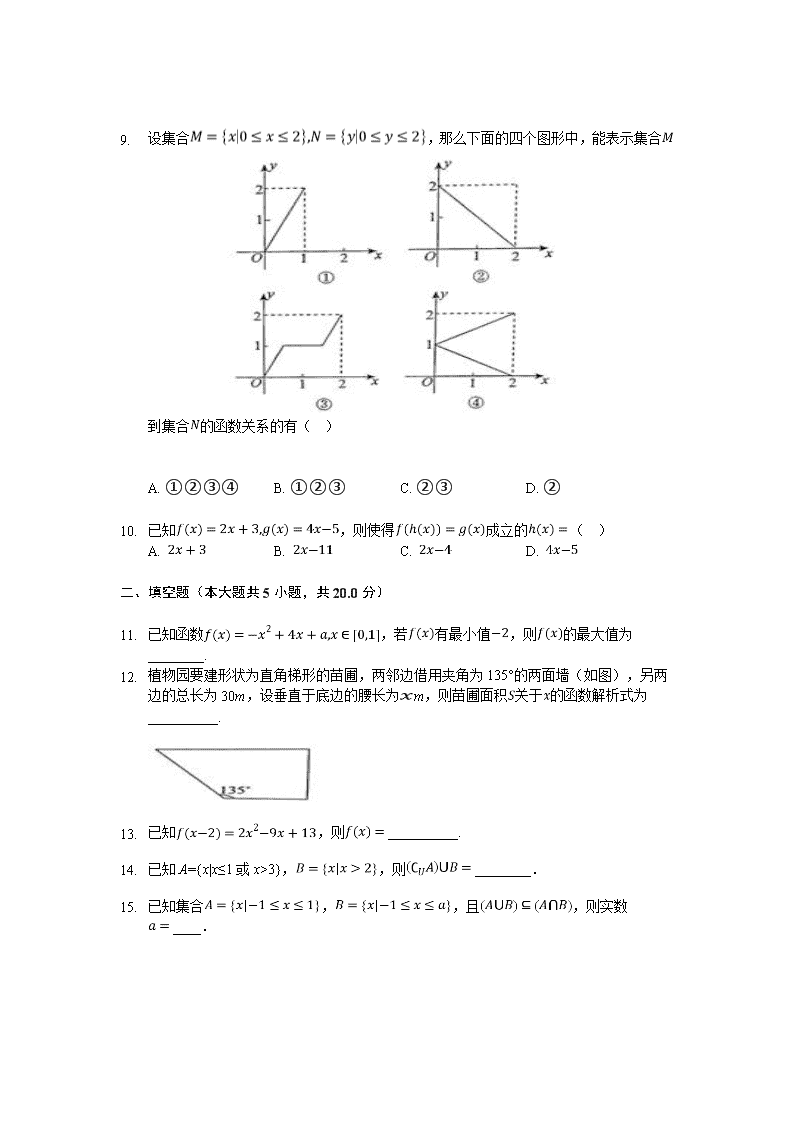
‎2019-2020学年湖南省湘南中学高一入学考试数学试题 题号 一 二 三 总分 得分 一、选择题（本大题共10小题，共40.0分）‎ 1. 若a是集合中的元素，但不是集合中的元素，则a可以是（   ）‎ A. 3.14 B. C. D. ‎ 2. 已知，则等于（   ）‎ A. B. C. D. ‎ 3. 函数的值域是（   ）‎ A. B. C. D. ‎ 4. 设函数在区间上都是增函数，则下列说法中：‎ ‎①是增函数；              ②是增函数；‎ ‎③是增函数；               ④是增函数.‎ 所有正确说法的个数是（   ）‎ A. 1 B. 2 C. 3 D. 4‎ 5. 下列函数在上是增函数的是（   ）‎ A. B. C. D. ‎ 6. 已知集合，，则中（  ）‎ A. 仅有一个元素 B. 至多有一个元素 C. 至少有一个元素 D. 可能有两个元素 7. 下列六个关系式中正确的个数是（）‎ ‎（1）   （2）   （3）‎ ‎（4）    （5）    （6）‎ A. 1 B. 2 C. 3 D. 4‎ 8. 设，，为非空集合的子集，且，，则与的关系是（   ）‎ A. B. C. D. ‎ 1. 设集合，那么下面的四个图形中，能表示集合到集合的函数关系的有（   ）‎ ‎ ‎ A. ①②③④ B. ①②③ C. ②③ D. ②‎ 2. 已知，则使得成立的（   ）‎ A. B. C. D. ‎ 二、填空题（本大题共5小题，共20.0分）‎ 3. 已知函数，若有最小值，则的最大值为________.‎ 4. 植物园要建形状为直角梯形的苗圃，两邻边借用夹角为135°的两面墙（如图），另两边的总长为30m，设垂直于底边的腰长为m，则苗圃面积关于的函数解析式为__________. ‎ 5. 已知，则__________.‎ 6. 已知A={x|x≤1或x>3}，，则________．‎ 7. 已知集合，，且，则实数____．‎ 三、解答题（本大题共5小题，共40.0分）‎ 1. ‎（6分）用列举法表示集合. ‎ 2. ‎（8分）设集合，，若，求实数的值． ‎ 3. ‎（8分）设，，，求：‎ ‎（1）；‎ ‎（2）． ‎ 4. ‎（8分）求函数的定义域，并用区间表示. ‎ 1. ‎（10分）如图，该曲线表示一人骑自行车离家的距离与时间的关系．骑车者9时离开家，15时回家．根据这个曲线图，请你回答下列问题： ‎ ‎（1）最初到达离家最远的地方是什么时间？离家多远？‎ ‎（2）何时开始第一次休息？休息多长时间？‎ ‎（3）第一次休息时，离家多远？‎ ‎（4）11：00到12：00他骑了多少千米？‎ ‎（5）他在9：00～10：00和10：00～10：30的平均速度分别是多少？ ‎ 答案和解析 ‎1. D 2. B 3.D 4.A 5.B 6.B 7.C 8.B 9. C 10.C ‎11.1 12. ()() 13. 14.​ 15.【答案】1‎ ‎16.【答案】解：由. 可得满足方程的解有， ​故方程的解集为． 17.【答案】解:因为，所以． 因为， 所以或． 当时，方程无解，此时． 当时，此时， 则．所以，即有，得． 综上，得或． 18.【答案】解：由题意可知． （1）因为， 所以; （2）又因为， 所以． 所以． 19.【答案】解：要使函数解析式有意义， 需满足解得且.   所以函数的定义域是{或}.    用区间表示为[)(]. ‎ ‎20.【答案】解：(1)最初到达离家最远的地方的时间是12时，离家30千米. (2)10：30开始第一次休息，休息了半小时. (3)第一次休息时，离家17千米. (4)11:00至12:00他骑了13千米. (5)9:00～10:00的平均速度10千米/时；10:00～10:30的平均速度是14千米/时. ‎