2021届浙江新高考数学一轮复习教师用书:第四章 5 第5讲 三角函数的图象与性质
第5讲 三角函数的图象与性质
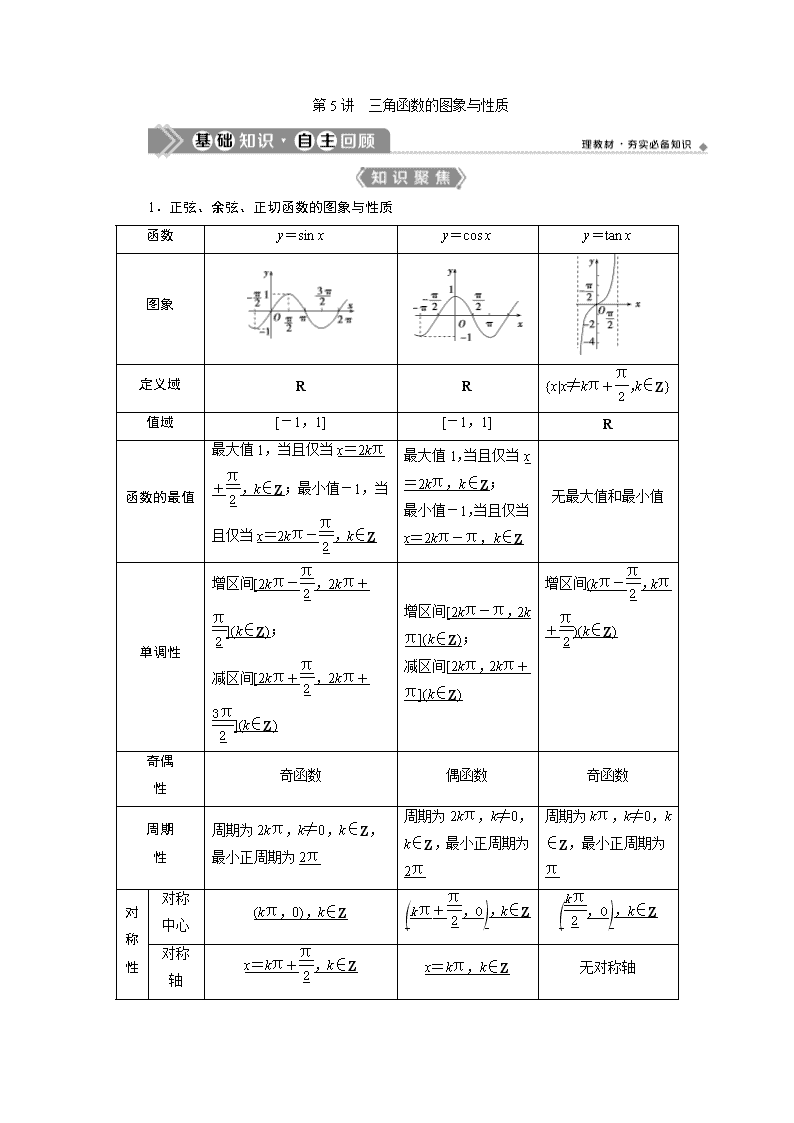
1.正弦、余弦、正切函数的图象与性质
函数
y=sin x
y=cos x
y=tan x
图象
定义域
R
R
{x|x≠kπ+,k∈Z}
值域
[-1,1]
[-1,1]
R
函数的最值
最大值1,当且仅当x=2kπ+,k∈Z;最小值-1,当且仅当x=2kπ-,k∈Z
最大值1,当且仅当x=2kπ,k∈Z;
最小值-1,当且仅当x=2kπ-π,k∈Z
无最大值和最小值
单调性
增区间[2kπ-,2kπ+](k∈Z);
减区间[2kπ+,2kπ+](k∈Z)
增区间[2kπ-π,2kπ](k∈Z);
减区间[2kπ,2kπ+π](k∈Z)
增区间(kπ-,kπ+)(k∈Z)
奇偶
性
奇函数
偶函数
奇函数
周期
性
周期为2kπ,k≠0,k∈Z,最小正周期为2π
周期为2kπ,k≠0,k∈Z,最小正周期为2π
周期为kπ,k≠0,k∈Z,最小正周期为π
对称性
对称
中心
(kπ,0),k∈Z
,k∈Z
,k∈Z
对称轴
x=kπ+,k∈Z
x=kπ,k∈Z
无对称轴
零点
kπ,k∈Z
kπ+,k∈Z
kπ,k∈Z
2.周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期;函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的周期均为T=;函数y=Atan(ωx+φ)的周期为T=.
3.对称与周期
正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是四分之一个周期;正切曲线相邻的两个对称中心之间的距离是半个周期.
[疑误辨析]
判断正误(正确的打“√”,错误的打“×”)
(1)y=cos x在第一、二象限内是减函数.( )
(2)若y=ksin x+1,x∈R,则y的最大值是k+1.( )
(3)若非零实数T是函数f(x)的周期,则kT(k是非零整数)也是函数f(x)的周期.( )
(4)函数y=sin x图象的对称轴方程为x=2kπ+(k∈Z).( )
(5)函数y=tan x在整个定义域上是增函数.( )
答案:(1)× (2)× (3)√ (4)× (5)×
[教材衍化]
1.(必修4P46A组T2,3改编)若函数y=2sin 2x-1的最小正周期为T,最大值为A,则T=________,A=________.
解析:最小正周期T==π,最大值A=2-1=1.
答案:π 1
2.(必修4P40练习T4改编)下列关于函数y=4sin x,x∈[-π,π]的单调性的叙述,正确的是________(填序号).
①在[-π,0]上是增函数,在[0,π]上是减函数;
②在上是增函数,在及上是减函数;
③在[0,π]上是增函数,在[-π,0]上是减函数;
④在及上是增函数,在上是减函数.
解析:函数y=4sin x在和上单调递减,在上单调递增.
答案:②
3.(必修4P45练习T3改编)y=tan 2x的定义域是________.
解析:由2x≠kπ+,k∈Z,得x≠+,k∈Z,所以y=tan 2x的定义域是.
答案:
[易错纠偏]
(1)忽视y=Asin x(或y=Acos x)中A对函数单调性的影响;
(2)忽视定义域的限制;
(3)忽视正切函数的周期;
(4)不化为同名函数以及同一单调区间导致比较大小出错.
1.函数y=1-2cos x的单调递减区间为________.
解析:函数y=1-2cos x的单调递减区间为函数y=cos x的递增区间.
答案:[-π+2kπ,2kπ](k∈Z)
2.函数f(x)=3sin(2x-)在区间[0,]上的值域为________.
解析:当x∈[0,]时,2x-∈[-,],
所以sin∈[-,1],
故3sin∈[-,3],
所以函数f(x)在区间[0,]上的值域是[-,3].
答案:[-,3]
3.函数y=tan图象的对称中心是________.
解析:由x+=,得x=-,k∈Z.
答案:(k∈Z)
4.cos 23°,sin 68°,cos 97°的大小关系是________.
解析:sin 68°=cos 22°,
又y=cos x在[0°,180°]上是减函数,
所以sin 68°>cos 23°>cos 97°.
答案:sin 68°>cos 23°>cos 97°
三角函数的定义域和值域
(1)函数f(x)=sin2x+cos x-的最大值是________.
(2)函数y=lg(2sin x-1)+的定义域是________.
【解析】 (1)依题意,f(x)=sin2x+cos x-=-cos2x+cos x+=-+1,
因为x∈,所以cos x∈[0,1],
因此当cos x=时,f(x)max=1.
(2)要使函数y=lg(2sin x-1)+有意义,
则
即
解得2kπ+≤x<2kπ+,k∈Z.
即函数的定义域为,k∈Z.
【答案】 (1)1 (2),k∈Z
(1)三角函数定义域的求法
求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.
(2)三角函数值域的不同求法
①利用sin x和cos x的值域直接求;
②把所给的三角函数式变换成y=Asin(ωx+φ)的形式求值域;
③(换元法)把sin x或cos x看作一个整体,转换成二次函数求值域;
④(换元法)利用sin x±cos x和sin xcos x的关系转换成二次函数求值域.
(2020·温州市十校联合体期初)已知函数f(x)=2cos x·(sin x-cos x),x∈R,则f=________,f(x)的最大值是________.
解析:f(x)=2cos x(sin x-cos x)
=2cos xsin x-2cos2x
=sin 2x-1-cos 2x
=sin-1.
当x=时,f=sin-1=0.
由正弦函数的图象和性质可得,sin的最大值为1.
所以f(x)的最大值为-1.
答案:0 -1
三角函数的单调性(高频考点)
三角函数的单调性是每年高考命题的热点,题型既有选择题也有填空题,或在解答题某一问出现,难度为中档题.主要命题角度有:
(1)求已知三角函数的单调区间;
(2)已知三角函数的单调区间求参数;
(3)利用三角函数的单调性比较大小;
(4)利用三角函数的单调性求值域(或最值).
角度一 求已知三角函数的单调区间
已知函数f(x)=sin2x-cos2x-2sin xcos x(x∈R).
(1)求f的值;
(2)求f(x)的最小正周期及单调递增区间.
【解】 (1)由sin =,cos =-,f=--2××,得f=2.
(2)由cos 2x=cos2x-sin2x与sin 2x=2sin xcos x得
f(x)=-cos 2x-sin 2x=-2sin.
所以f(x)的最小正周期是π.
由正弦函数的性质得+2kπ≤2x+≤+2kπ,
k∈Z,解得+kπ≤x≤+kπ,k∈Z,
所以,f(x)的单调递增区间是(k∈Z).
角度二 已知三角函数的单调区间求参数
函数f(x)=sin(x+φ)在区间上单调递增,则常数φ的值可能是( )
A.0 B.
C.π D.
【解析】 法一:结合选项,当φ分别取选项中的值时,
A:f(x)=sin x;B:f(x)=cos x;C:f(x)=-sin x;D:f(x)=-cos x.验证得D选项正确.
法二:⊆f(x)的递增区间,
⊆,
⇒-+2kπ≤φ≤-+2kπ(k∈Z),
k=0,选项中无值符合;k=1,≤φ≤,φ=符合;
k=2,≤φ≤,选项中无值符合.可知φ的可取值逐渐增大,故只有D选项符合题意.
【答案】 D
角度三 利用三角函数的单调性比较大小
已知函数f(x)=2sin,设a=f,b=f,c=f,则a,b,c的大小关系是( )
A.a
0时,由题意知-ω≤-,
即ω≥;
当ω<0时,由题意知ω≤-,所以ω≤-2.
综上可知,ω的取值范围是∪.
2.函数f(x)=sin在区间上的最小值为 ( )
A.-1 B.-
C. D.0
解析:选B.由已知x∈,得2x-∈,所以sin∈,故函数f(x)=sin(2x-)在区间上的最小值为-.
3.函数y=sin的单调减区间为________.
解析:(同增异减法)y=-sin,
它的减区间是y=sin的增区间.
由2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.
故其单调减区间为,k∈Z.
答案:(k∈Z)
三角函数的奇偶性、周期性及对称性
(1)设函数f(x)=sin2 x+bsin x+c,则f(x)的最小正周期( )
A.与b有关,且与c有关
B.与b有关,但与c无关
C.与b无关,且与c无关
D.与b无关,但与c有关
(2)已知ω>0,f(x)=,f的图象与f(x)的图象关于点对称,则ω的最小值为( )
A. B.1
C. D.2
(3)已知函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,0<φ<π)是奇函数,直线y=与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为,则( )
A.f(x)在上单调递减
B.f(x)在上单调递减
C.f(x)在上单调递增
D.f(x)在上单调递增
【解析】 (1)由于f(x)=sin2x+bsin x+c=+bsin x+c.当b=0时,f(x)的最小正周期为π;当b≠0时,f(x)的最小正周期为2π.c的变化会引起f(x)图象的上下平移,不会影响其最小正周期.故选B.
(2)因为f(x)==tan,
所以f=tan,
因为f的图象与f(x)的图象关于点对称,
所以tan+tan=0,
即tan=tan,
所以=-ωπ-+kπ,(k∈Z),ω=-+k,(k∈Z),
因为ω>0,所以当k=1时,ω取最小值为,故选A.
(3)f(x)=sin(ωx+φ)+cos(ωx+φ)=sin(ωx+φ+),因为0<φ<π且f(x)为奇函数,所以φ=,即f(x)=-sin ωx,又直线y=与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为,所以函数f(x)的最小正周期为,由=,可得ω=4,故f(x)=-sin 4x,由2kπ+≤4x≤2kπ+,k∈Z,即+≤x≤+,k∈Z,令k=0,得≤x≤,此时f(x)在上单调递增.
【答案】 (1)B (2)A (3)D
三角函数的奇偶性、对称性和周期问题的解题思路
(1)奇偶性的判断方法:三角函数中奇函数一般可化为y=Asin ωx或y=Atan ωx
的形式,而偶函数一般可化为y=Acos ωx+b的形式.
(2)周期的计算方法:利用函数y=Asin(ωx+φ)(ω>0),y=Acos(ωx+φ)(ω>0)的周期为,函数y=Atan(ωx+φ)(ω>0)的周期为求解.
(3)解决对称性问题的关键:熟练掌握三角函数的对称轴、对称中心.
[提醒] 对于函数y=Asin(ωx+φ),其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断直线x=x0或点(x0,0)是否是函数的对称轴或对称中心时,可通过检验f(x0)的值进行判断.
1.(2020·舟山市普陀三中高三期中)设函数f(x)=sin(2x+φ)+cos(2x+φ)为偶函数,则φ=( )
A. B.
C. D.
解析:选C.f(x)=sin(2x+φ)+cos(2x+φ)=sin,
因为函数f(x)为偶函数,
所以f(-x)-f(x)
=sin-sin=0,
即sin=sin,
所以-2x+φ+=2x+φ++2kπ,或-2x+φ++2x+φ+=π+kπ,
即x=-,k∈Z(舍)或φ=+,k∈Z.
因为|φ|<,所以φ=.
2.(2020·浙江省名校协作体高三联考)已知函数f(x)=sin 2x(1-2sin2x)+1,则f(x)的最小正周期T=________,f(T)=________.
解析:由题意得,f(x)=sin 2xcos 2x+1=sin 4x+1,所以最小正周期T==,f(T)=f=1.
答案: 1
3.已知函数f(x)=sin x的图象与直线kx-y-kπ=0(k>0)恰有三个公共点,这三个点的横坐标从小到大分别为x1,x2,x3,则=________.
解析:如图所示,易知x2=π,x1+x3=2x2=2π,
则k==,
又直线与y=sin x相切于点A(x3,sin x3),
则k=cos x3,
则=cos x3⇒==,故答案为.
答案:
核心素养系列7 数学抽象——三角函数中ω值的求法
一、利用三角函数的单调性求解
若函数f(x)=sin ωx(ω>0)在区间上单调递减,则ω的取值范围是________.
【解析】 令+2kπ≤ωx≤+2kπ(k∈Z),得+≤x≤+,因为f(x)在上单调递减,所以得6k+≤ω≤4k+3.又ω>0,所以k≥0,又6k+<4k+3,得0≤k<,所以k=0.即≤ω≤3.
【答案】
根据正弦函数的单调递减区间,确定函数f(x)的单调递减区间,根据函数f(x)=sin ωx(ω>0)在区间上单调递减,建立不等式,即可求ω的取值范围.
二、利用三角函数的对称性求解
(1)已知函数f(x)=cos(ω>0)的一条对称轴为x=,一个对称中心为点,则ω有( )
A.最小值2 B.最大值2
C.最小值1 D.最大值1
(2)若函数y=cos(ω∈N*)图象的一个对称中心是,则ω的最小值为________.
【解析】 (1)因为函数的中心到对称轴的最短距离是,两条对称轴间的最短距离是,所以中心到对称轴x=间的距离用周期可表示为-=+(k∈N,T为周期),解得(2k+1)T=π,又T=,所以(2k+1)·=π,则ω=2(2k+1),当k=0时,ω=2最小.故选A.
(2)依题意得cos=0,则+=+kπ(k∈Z)⇒ω=6k+2(k∈Z),又ω∈N*,所以ω的最小值为=2.
【答案】 (1)A (2)2
三角函数两条相邻对称轴或两个相邻对称中心之间的“水平间隔”为,相邻的对称轴和对称中心之间的“水平间隔”为,这就说明,我们可根据三角函数的对称性来研究其周期性,进而可以研究“ω”的取值.值得一提的是,三角函数的对称轴必经过其图象上的最高点(极大值)或最低点(极小值),函数f(x)=Asin(ωx+φ)的对称中心就是其图象与x轴的交点,这就说明,我们也可利用三角函数的极值点(最值点)、零点之间的“差距”来确定其周期,进而可以确定“ω”的取值.
三、利用三角函数的最值求解
已知f(x)=sin(ωx+)(ω>0),f=f(),且f(x)在区间内有最小值无最大值,则ω=________.
【解析】 因为f=f,而=,所以f(x)的图象关于直线x=对称,又f(x)在区间内有最小值无最大值,所以f(x)min=f=sin=-1,所以+
eq f(π,3)=kπ+,k∈Z,解得ω=4k+.再由f(x)在区间内有最小值无最大值,得≥-,解得ω≤6,所以k=0,ω=.
【答案】
利用三角函数的最值与对称或周期的关系,可以列出关于ω的不等式,进而求出ω的值或取值范围.
[基础题组练]
1.最小正周期为π且图象关于直线x=对称的函数是( )
A.y=2sin B.y=2sin
C.y=2sin D.y=2sin
解析:选B.由函数的最小正周期为π,可排除C.由函数图象关于直线x=对称知,该直线过函数图象的最高点或最低点,对于A,因为sin=sin π=0,所以选项A不正确.对于D,sin=sin=,所以D不正确,对于B,sin=sin=1,所以选项B正确,故选B.
2.(2020·合肥市第一次教学质量检测)函数y=sin(ωx+)在x=2处取得最大值,则正数ω的最小值为( )
A. B. C. D.
解析:选D.由题意得,2ω+=+2kπ(k∈Z),解得ω=+kπ(k∈Z),因为ω>0,所以当k=0时,ωmin=,故选D.
3.(2020·浙江省名校协作体高三联考)下列四个函数:y=sin|x|,y=cos|x|,y=|tan x|,y=-ln|sin x|,以π为周期,在上单调递减且为偶函数的是( )
A.y=sin|x| B.y=cos|x|
C.y=|tan x| D.y=-ln|sin x|
解析:选D.A.y=sin|x|在上单调递增,故A错误;B.y=cos|x|=cos x周期为T=2π,故B错误;C.y=|tan x|在上单调递增,故C错误;D.f(x+π)=-ln|sin(x+π)|=-ln|sin x|,周期为π,当x∈时,y=-ln(sin x)是在上单调递减的偶函数,故D正确,故选D.
4.设函数f(x)=cos(x+),则下列结论错误的是( )
A.f(x)的一个周期为-2π
B.y=f(x)的图象关于直线x=对称
C.f(x+π)的一个零点为x=
D.f(x)在(,π)上单调递减
解析:选D.根据函数解析式可知函数f(x)的最小正周期为2π,所以函数的一个周期为-2π,A正确;当x=时,x+=3π,所以cos=-1,所以B正确;f(x+π)=cos=cos,当x=时,x+=,所以f(x+π)=0,所以C正确;函数f(x)=cos在上单调递减,在上单调递增,故D不正确.所以选D.
5.若函数f(x)=sin(ω>0)在区间(π,2π)内没有最值,则ω的取值范围是( )
A.∪ B.∪
C. D.
解析:选B.易知函数y=sin x的单调区间为
[kπ+,kπ+],k∈Z,
由kπ+≤ωx+≤kπ+,k∈Z,得≤x≤,k∈Z,
因为函数f(x)=sin(ω>0)在区间(π,2π)内没有最值,
所以f(x)在区间(π,2π)内单调,
所以(π,2π)⊆,k∈Z,
所以k∈Z,解得k+≤ω≤+,k∈Z,
由k+≤+,得k≤,
当k=0时,得≤ω≤;
当k=-1时,得-≤ω≤.
又ω>0,所以0<ω≤.
综上,得ω的取值范围是∪.故选B.
6.已知函数f(x)=sin,f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A. B.
C. D.
解析:选A.由题意,得f′(x)=2cos,所以y=2f(x)+f′(x)=2sin+2cos=2sin=2sin.由2kπ+≤2x+≤2kπ+(k∈Z),得kπ+≤x≤kπ+(k∈Z),所以y=2f(x)+f′(x)的一个单调递减区间为,故选A.
7.函数y=lg sin x+ 的定义域为________.
解析:要使函数有意义,则有
即解得(k∈Z),
所以2kπ0),直线y=与函数f(x)图象相邻两交点的距离为π.
(1)求ω的值;
(2)在△ABC中,角A、B、C所对的边分别是a、b、c,若点是函数y=f(x)图象的一个对称中心,且b=3,求△ABC面积的最大值.
解:(1)函数f(x)=sin-2cos2x+1
=sin ωxcos-cos ωxsin-2·+1
=sin ωx-cos ωx=sin.
因为f(x)的最大值为,所以f(x)的最小正周期为π,
所以ω=2.
(2)由(1)知f(x)=sin,
因为sin=0⇒B=,
因为cos B===,
所以ac=a2+c2-9≥2ac-9,ac≤9,
故S△ABC=acsin B=ac≤.
故△ABC面积的最大值为.
5.已知a>0,函数f(x)=-2asin+2a+b,当x∈时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f且lg g(x)>0,求g(x)的单调区间.
解:(1)因为x∈,所以2x+∈.
所以sin∈,
所以-2asin∈[-2a,a].
所以f(x)∈[b,3a+b],又因为-5≤f(x)≤1,
所以b=-5,3a+b=1,因此a=2,b=-5.
(2)由(1)得,f(x)=-4sin-1,
g(x)=f=-4sin-1
=4sin-1,
又由lg g(x)>0,得g(x)>1,所以4sin-1>1,
所以sin>,
所以2kπ+<2x+<2kπ+,k∈Z,
其中当2kπ+<2x+≤2kπ+,k∈Z时,g(x)单调递增,即kπ
查看更多