高考数学复习专题练习第1讲 函数及其表示
第二章 函数与基本初等函数I
第1讲 函数及其表示
一、选择题
1.设函数f(x)=2x+3,g(x+2)=f(x),则g(x)的表达式是( )
A.g(x)=2x+1 B.g(x)=2x-1
C.g(x)=2x-3 D.g(x)=2x+7
解析 ∵g(x+2)=2x+3=2(x+2)-1,∴g(x)=2x-1.
答案 B
2.下列函数中,与函数y=定义域相同的函数为 ( ).
A.y= B.y=
C.y=xex D.y=
解析 函数y=的定义域为{x|x≠0,x∈R}与函数y=的定义域相同,故选D.
答案 D
3.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,则函数解析式为y=x2+1,值域为{1,3}的同族函数有 ( ).
A.1个 B.2个 C.3个 D.4个
解析 由x2+1=1,得x=0.由x2+1=3,得x=±,所以函数的定义域可以是{0,},{0,-},{0,,-},故值域为{1,3}的同族函数共有3个.
答案 C
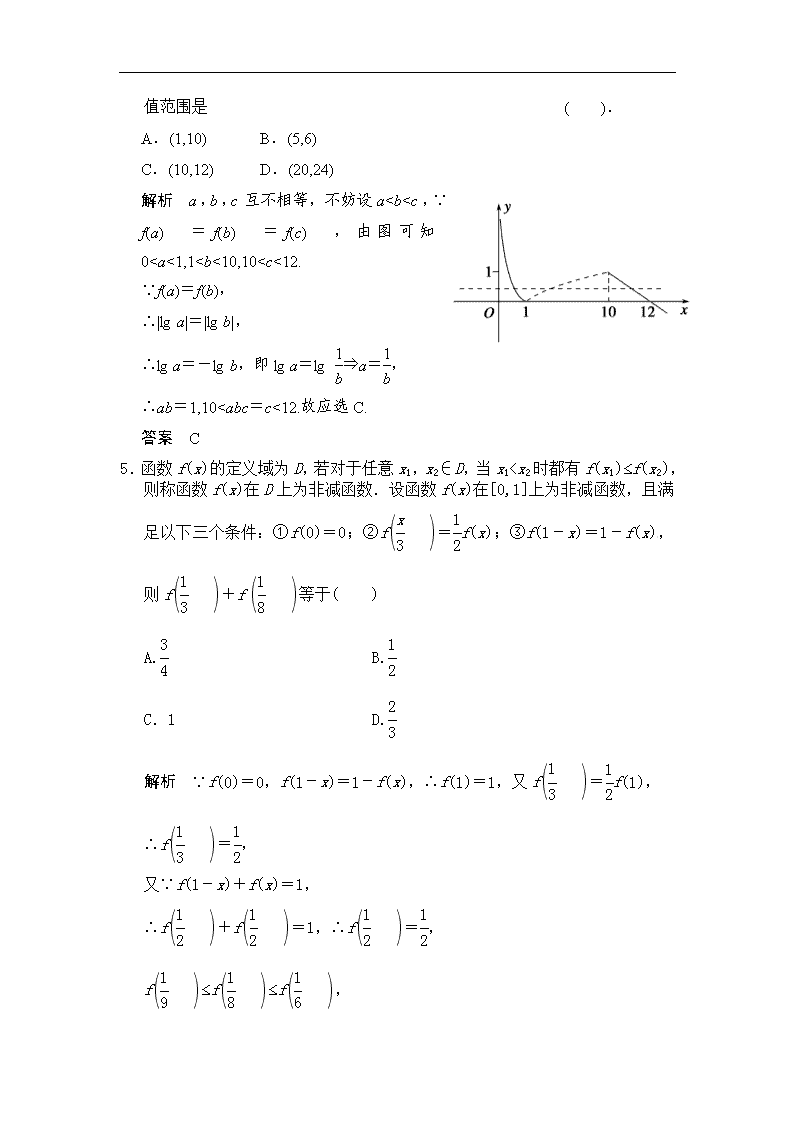
4.已知函数f(x)=若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是 ( ).
A.(1,10) B.(5,6)
C.(10,12) D.(20,24)
解析 a,b,c互不相等,不妨设a
-1的解集为( )
A.(-∞,-1)∪(1,+∞)
B.∪(0,1]
C.(-∞,0)∪(1,+∞)
D.∪(0,1)
解析 ①当-1≤x<0时,0<-x≤1,此时f(x)=-x-1,f(-x)=-(-x)+1=x+1,
∴f(x)-f(-x)>-1化为-2x-2>-1,
得x<-,则-1≤x<-.
②当0-1化为-x+1-(x-1)>-1,
解得x<,则01),则x=,
∴f(t)=lg,f(x)=lg(x>1),∴f(21)=-1.
答案 -1
8.函数y=-的值域为________.
解析 函数定义域为[1,+∞),
∵y=-=,
当x≥1时是减函数,∴0f(2x)的x的取值范围是________.
解析 由题意有或解得-10}=,
N==={x|x≥3,或x<1}.
(2)M∩N={x|x≥3},M∪N=.
12.二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[-1,1]上,函数y=f(x)的图像恒在直线y=2x+m的上方,试确定实数m的取值范围.
解 (1)由f(0)=1,可设f(x)=ax2+bx+1(a≠0),故f(x+1)-f(x)=a(x+1)2+b(x+1)+1-(ax2+bx+1)=2ax+a+b,由题意,得解得
故f(x)=x2-x+1.
(2)由题意,得x2-x+1>2x+m,即x2-3x+1>m,对x∈[-1,1]恒成立.令g(x)=x2-3x+1,则问题可转化为g(x)min>m,又因为g(x)在[-1,1]上递减, 所以g(x)min=g(1)=-1,故m<-1.
13.设函数f(x)=g(x)=f(x)-ax,
x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
(1)求函数h(a)的解析式;
(2)画出函数y=h(x)的图像并指出h(x)的最小值.
解 (1)由题意知g(x)=
当a<0时,函数g(x)是[1,3]上的增函数,此时g(x)max=g(3)=2-3a,g(x)min=g(1)=1-a,所以h(a)=1-2a;
当a>1时,函数g(x)是[1,3]上的减函数,此时g(x)min=g(3)=2-3a,g(x)max=g(1)=1-a,所以h(a)=2a-1;
当0≤a≤1时,若x∈[1,2],则g(x)=1-ax,有g(2)≤g(x)≤g(1);
若x∈(2,3],则g(x)=(1-a)x-1,有g(2)8),
则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和.
-(t3-3)++=4,
解得t3=10.5(小时)>10小时故舍去.