黑龙江省哈尔滨市阿城区龙涤中学校2019-2020学年高二上学期期中考试数学试题

黑龙江省哈尔滨市阿城区龙涤中学校2019-2020学年高二上学期期中考试数学试题

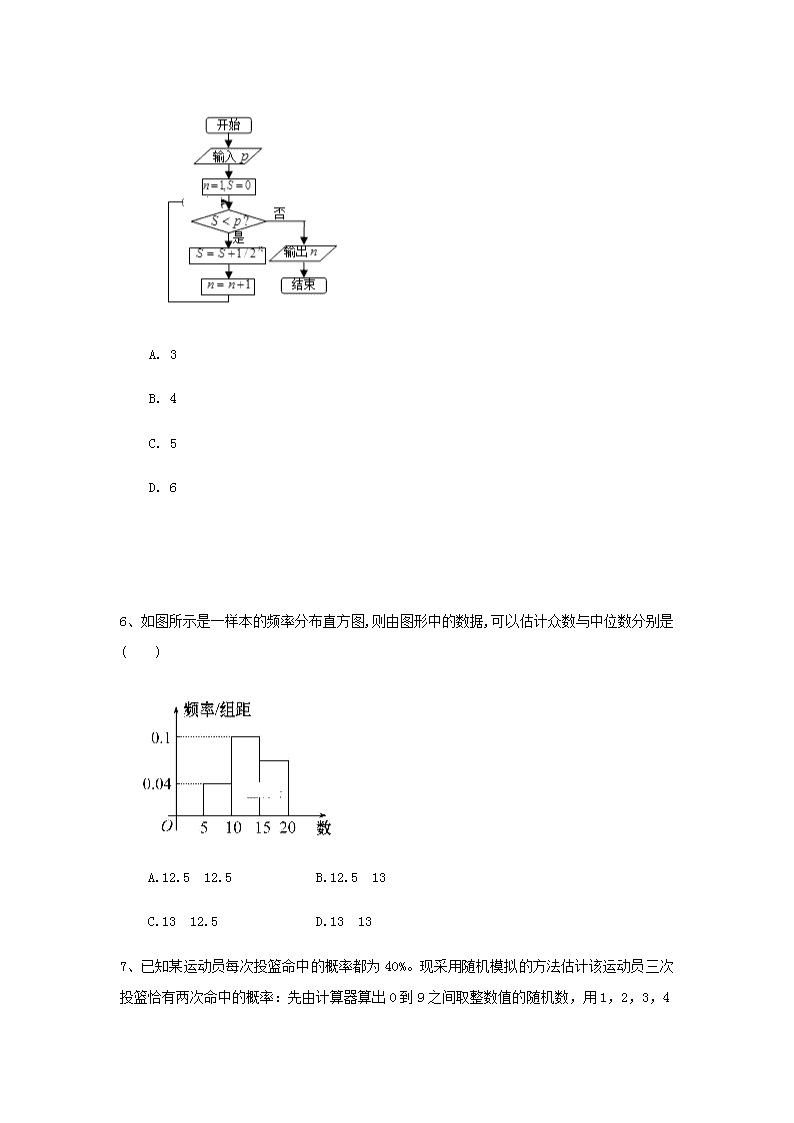
数学试题 注意事项：‎ ‎1．答题前，考生必须将自己的姓名、准考号、班级和登录账号填写在答题纸和答题卡的指定位置．‎ ‎2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效．‎ ‎3．非选择题必须使用0.5毫米黑色字迹的签字笔书写，字迹工整，笔迹清楚，请按照题号顺序在各个题目的答题区域作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1、若命题“”为假，且“”为假，则(　　)‎ A.假B.“”为假C.真 D.不能判断的真假 ‎2、如果椭圆上一点P到焦点的距离为6，则点P到另一个焦点的距离为(　　)‎ A.10 B.6 C.12 D.14‎ ‎3、已知直线y=x+b,b∈[-2,3],则直线在y轴上的截距大于1的概率为(　　)‎ A. B. C. D.‎ ‎4、根据一组数据(24,25),(26,25),(26,26),(26,27),(28,27),用最小二乘法建立的回归直线方程为=kx+13,则k=(　　)‎ A.2　　　B.4　　　C.　　　D.‎ ‎5、阅读右图所示的程序框图，运行相应的程序，若，则输出的值为(　　)‎ A. 3 ‎ B. 4 ‎ C. 5 ‎ D. 6‎ ‎6、如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是(　　)‎ A.12.5　12.5 B.12.5　13‎ C.13　12.5 D.13　13 ‎ ‎7、已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，用1，2，3，4表示命中，用5，6，，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果。经随机模拟产生了20组随机数：‎ ‎ 907 966 191 925 271 932 812 458 569 683‎ ‎ 431 257 393 027 556 488 730 113 537 989‎ 据此估计，该运动员三次投篮恰有两次命中的概率为(　　)‎ A.0.35 B.0.30 C.0.25 D.0.20‎ ‎8、命题“若或，则”的逆否命题是(　　)‎ A.若，则或B.若或，则 C.若，则且D.若且，则 ‎9、已知椭圆过点和点，则此椭圆的标准方程是(　　)‎ A． B．或 C． D．以上均不正确 ‎10、如果数据x1,x2,…,xn的平均数为,方差为s2,则5x1+2,5x2+2,…,5xn+2的平均数和方差分别为(　　)‎ A.,s2 B.5+2,s2‎ C.5+2,25s2 D.,25s2‎ ‎11、用秦九韶算法求多项式在 的值时，其中的值是(　　)‎ A.34 B.22 C.57 D.220‎ ‎12、已知、是椭圆的两个焦点，满足的点总在椭圆内部，则椭圆离心率的取值范围是(　　)‎ A.B.C. D.‎ 第Ⅱ卷（非选择题，共70分）‎ 二、填空题（本题共4小题，每小题5分，共20分，把正确答案填在答题卡的横线上）‎ ‎13、若方程表示椭圆，则m的取值范围是．‎ ‎14、已知椭圆的左右两个焦点分别为，是椭圆上一点，且，则△的面积为． [来源:学科网ZXXK]‎ ‎15、已知圆,则过点且与圆C相切的直线方程为．‎ ‎16、给出下列结论：‎ ‎①命题“”的否定是“”；‎ ‎②命题“所有正方形都是平行四边形”的否定是“所有正方形都不是平行四边形”；‎ ‎③命题“是互斥事件”是命题“是对立事件”的必要不充分条件；‎ ‎④若，是实数，则“且”是“且”的充分不必要条件.‎ 其中正确结论的是．‎ 三、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17、（本题满分10分）某车间20名工人年龄数据如下表:‎ 年龄(岁)‎ 工人数(人)‎ ‎19‎ ‎1‎ ‎28‎ ‎3‎ ‎29‎ ‎3‎ ‎30‎ ‎5‎ ‎31‎ ‎4‎ ‎32‎ ‎3‎ ‎40‎ ‎1‎ 合计 ‎20‎ ‎(1)求这20名工人年龄的众数与极差; (2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图; (3)求这20名工人年龄的方差.‎ ‎18、（本题满分12分）某初级中学共有学生2000名,各年级男生、女生人数如表:‎ 初一年级 初二年级 初三年级 女生 ‎373‎ x y 男生 ‎377‎ ‎370‎ z 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.[来源:学科网ZXXK]‎ ‎(1)求x的值.‎ ‎(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?‎ ‎(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.‎ ‎19、（本题满分12分）已知离心率为的椭圆C:+=1(a>b>0)过点M(,1).‎ ‎(1)求椭圆的方程.‎ ‎(2)已知与圆x2+y2=相切的直线l与椭圆C相交于不同两点A,B,O为坐标原点,求 ‎·的值.‎ ‎20、（本题满分12分）A,B,C,D,E五位学生的数学成绩x与物理成绩y(单位:分)如表:‎ x ‎80‎ ‎75‎ ‎70‎ ‎65‎ ‎60‎ y ‎70‎ ‎66‎ ‎68‎ ‎64‎ ‎62‎ ‎(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程=x+;(参考数值:80×70+75×66+70×68+65×64+60×62=23190,802+752+702+652+602=24750)‎ ‎(2)若学生F的数学成绩为90分,试根据(1)求出的回归方程,预测其物理成绩(结果保留整数).‎ 用最小二乘法求线性回归方程系数公式：‎ ‎21、（本题满分12分）为了估计某校某次数学考试的情况,现从该校参加考试的600名学生中随机抽出60名学生,其数学成绩(百分制)均在 [40,100]内,将这些成绩分成六组[40,50),[50, 60),…,[90,100],得到如图所示的部分频率分布直方图.‎ ‎(1)求抽出的60名学生中数学成绩在[70,80)内的人数;[来源:学#科#网]‎ ‎(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校参加考试的学生数学成绩为优秀的人数;‎ ‎(3)试估计抽出的60名学生的数学成绩的中位数.‎ ‎22、（本题满分12分）已知椭圆：的左、右焦点为、，椭圆上的点 满足．‎ ‎(1)求椭圆的标准方程；‎ ‎(2)自定点作一条直线与椭圆交于不同的两点、（点在点的下方），记，求的取值范围．‎ 参考答案 一、 选择题：ADBCB BCCAC AD 二、 填空题：（13） （14） （15） （16）①③‎ 三、 解答题 ‎17、答案：（1）这名工人年龄的众数为:;这名工人年龄的极差为:. （2）以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图如图. （3）这名工人年龄的平均数为:; 所以这名工人年龄的方差为: .‎ ‎18、【解析】(1)由=0.19,得x=380.‎ ‎(2)初三年级人数为y+z=2000-(373+377+380+370)=500,‎ 现用分层抽样法在全校抽取48名学生,应在初三年级学生中抽取的人数为×500=12,即抽取初三年级学生12名.‎ ‎(3)记“初三年级女生比男生多”为事件A,‎ 由(2)知y+z=500,‎ 又已知y≥245,z≥245,‎ 则所有的基本事件(前一个数表示女生人数,后一个数表示男生人数)有(245,255),(246,254),(247,253),…,(255,245),共11个.‎ 其中事件A包含的基本事件有(251,249),(252,248),(253,247),(254,246),‎ ‎(255,245),共5个,则P(A)=.‎ ‎19、【解析】(1)因为e=,又椭圆C过点M(,1),‎ 所以解得 所以椭圆方程为+=1.‎ ‎(2)设A(x1,y1),B(x2,y2),‎ 当直线l的斜率不存在时,l:x=±,‎ 则x1=x2=±,y1=-y2,‎ 所以·=-=0.‎ 当直线l的斜率存在时,设l:y=kx+m,‎ 由于l与圆相切得:=,‎ 所以3m2-8k2-8=0.‎ 将l的方程代入椭圆方程得:‎ ‎(1+2k2)x2+4kmx+2m2-8=0,‎ 所以x1+x2=-,x1·x2=,‎ 所以·=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2==0,‎ 综上,·=0.‎ ‎20、解：【解析】(1)因为==70,‎ ‎==66,‎ xiyi=80×70+75×66+70×68+65×64+60×62‎ ‎=23190,‎ =802+752+702+652+602=24750,‎ 所以===0.36,‎ ‎=-=66-0.36×70=40.8.‎ 故所求线性回归方程为=0.36x+40.8.‎ ‎(2)由(1),当x=90时,=0.36×90+40.8=73.2≈73,‎ 答:预测学生F的物理成绩为73分.‎ ‎21、答案：（1）成绩在内的频率为 所以名学生中数学成绩在内的人数为. （2）估计该校参加考试的学生数学成绩为优秀的人数为. （3）抽出名学生中分数在内的人数为,分数在内的频率为,所以中位数落在内故中位数约为.‎ ‎22、解：（1）设，其中，于是，，则由可得，‎ 所以．………………………………………………………2分 又点在椭圆上，所以，即．………… 又，所以，．………… 代入整理得，解得（舍），或．‎ 所以，．‎ 于是，所求的椭圆的标准方程为．………………4分 ‎（2）由题可知，．‎ 于是，由，则，‎ ‎（I）当直线的斜率不存在时，‎ 容易求得，，‎ 所以，[来源:学*科*网Z*X*X*K]‎ 所以，此时．……………………5分 ‎（II）当直线的斜率存在时，设为，则直线的方程为． 设点，将代入消去得：‎ ‎．‎ 由解得．‎ ‎，………… ‎，………………………………………………………7分 又，所以，所以有 ‎，………………… 将代入得，………… 将代入得，……………… 联立，消去得，‎ 所以，，化简得，‎ 因为，，所以，‎ 所以，且．………………9分 设，则在上为减函数，又，‎ 所以．（此处也可以通过解一元二次不等式求出的取值范围）‎ 综合（I）、（II）可得，的取值范围是．…………10分