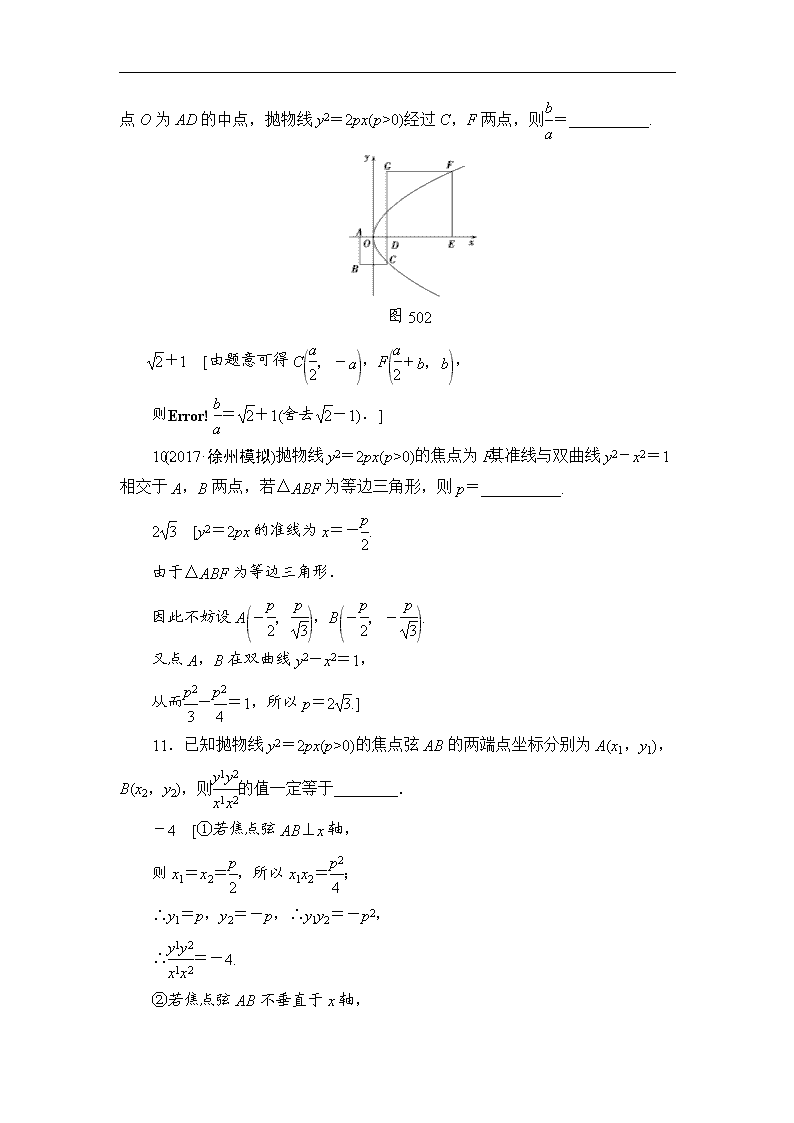高考数学 17-18版 第9章 第50课 课时分层训练50

高考数学 17-18版 第9章 第50课 课时分层训练50

课时分层训练(五十) A 组 基础达标 (建议用时：30 分钟) 1．(2016·四川高考改编)抛物线 y2＝4x 的焦点坐标是________． (1,0) [由 y2＝4x 知 p＝2，故抛物线的焦点坐标为(1,0)．] 2．已知点 F 是抛物线 C：y2＝4x 的焦点，点 A 在抛物线 C 上，若 AF＝4， 则线段 AF 的中点到抛物线 C 的准线的距离为________． 3 [由题意易知 F(1,0)，F 到准线的距离为 2，A 到准线的距离为 AF＝4，则 线段 AF 的中点到抛物线 C 的准线的距离为2＋4 2 ＝3.] 3．(2017·南京模拟)抛物线 y2＝4x 的焦点到双曲线 x2－y2 3 ＝1 的渐近线的距 离是________. 【导学号：62172276】 3 2 [由双曲线 x2－y2 3 ＝1 知其渐近线方程为 y＝± 3x，即 3x±y＝0， 又 y2＝4x 的焦点 F(1,0)， ∴焦点 F 到直线的距离 d＝ 3  32＋－12 ＝ 3 2 .] 4．已知抛物线 C 与双曲线 x2－y2＝1 有相同的焦点，且顶点在原点，则抛 物线 C 的方程是________． y2＝±4 2x [因为双曲线的焦点为(－ 2，0)，( 2，0)． 设抛物线方程为 y2＝±2px(p>0)，则p 2 ＝ 2，p＝2 2. 所以抛物线方程为 y2＝±4 2x.] 5．过抛物线 y2＝4x 的焦点 F 作倾斜角为 45°的直线交抛物线于 A，B 两点， 则弦长 AB 为__________． 8 [设 A(x1，y1)，B(x2，y2)．易得抛物线的焦点是 F(1,0)，所以直线 AB 的 方程是 y＝x－1. 联立 y2＝4x， y＝x－1， 消去 y 得 x2－6x＋1＝0. 所以 x1＋x2＝6，所以 AB＝x1＋x2＋p＝6＋2＝8.] 6．已知点 A(－2,3)在抛物线 C：y2＝2px 的准线上，记 C 的焦点为 F，则直 线 AF 的斜率为__________． －3 4 [∵点 A(－2,3)在抛物线 C 的准线上． ∴－p 2 ＝－2，∴p＝4，焦点 F(2,0)． ∴kAF＝ 3－0 －2－2 ＝－3 4.] 7．若抛物线 y2＝2px 的焦点与椭圆x2 9 ＋y2 5 ＝1 的右焦点重合，则该抛物线的 准线方程为__________． x＝－2 [由椭圆x2 9 ＋y2 5 ＝1，知 a＝3，b＝ 5， 所以 c2＝a2－b2＝4，所以 c＝2. 因此椭圆的右焦点为(2,0)， 又抛物线 y2＝2px 的焦点为 p 2 ，0 . 依题意，得p 2 ＝2， 于是抛物线的准线 x＝－2.] 8．设 P 是抛物线 y2＝4x 上的一个动点，则点 P 到点 A(－1,1)的距离与点 P 到直线 x＝－1 的距离之和的最小值为__________. 【导学号：62172277】 5 [如图，易知抛物线的焦点为 F(1,0)，准线是 x＝－1，由抛物线的定义 知：点 P 到直线 x＝－1 的距离等于点 P 到 F 的距离．于是，问题转化为在抛物 线上求一点 P，使点 P 到点 A(－1,1)的距离与点 P 到 F(1,0)的距离之和最小． 连结 AF 交抛物线于点 P，此时最小值为 AF＝ [1－－1]2＋0－12＝ 5.] 9．如图 502，正方形 ABCD 和正方形 DEFG 的边长分别为 a，b(a0)经过 C，F 两点，则b a ＝__________. 图 502 2＋1 [由题意可得 C a 2 ，－a ，F a 2 ＋b，b ， 则 a2＝pa， b2＝2p a 2 ＋b ， b a ＝ 2＋1(舍去 2－1)．] 10．(2017·徐州模拟)抛物线 y2＝2px(p>0)的焦点为 F，其准线与双曲线 y2－ x2＝1 相交于 A，B 两点，若△ABF 为等边三角形，则 p＝__________. 2 3 [y2＝2px 的准线为 x＝－p 2. 由于△ABF 为等边三角形． 因此不妨设 A －p 2 ， p 3 ，B －p 2 ，－ p 3 . 又点 A，B 在双曲线 y2－x2＝1， 从而p2 3 －p2 4 ＝1，所以 p＝2 3.] 11．已知抛物线 y2＝2px(p>0)的焦点弦 AB 的两端点坐标分别为 A(x1，y1)， B(x2，y2)，则y1y2 x1x2 的值一定等于________． －4 [①若焦点弦 AB⊥x 轴， 则 x1＝x2＝p 2 ，所以 x1x2＝p2 4 ； ∴y1＝p，y2＝－p，∴y1y2＝－p2， ∴y1y2 x1x2 ＝－4. ②若焦点弦 AB 不垂直于 x 轴， 可设 AB 的直线方程为 y＝k x－p 2 ， 联立 y2＝2px 得 k2x2－(k2p＋2p)x＋p2k2 4 ＝0，则 x1x2＝p2 4 .y1y2＝－p2，∴y1y2 x1x2 ＝ －4.] 12．设抛物线 C：y2＝2px(p>0)的焦点为 F，点 M 在 C 上，MF＝5.若以 MF 为直径的圆过点(0,2)，则 C 的方程为________. 【导学号：62172278】 y2＝4x 或 y2＝16x [由已知得抛物线的焦点 F p 2 ，0 ，设点 A(0,2)，点 M(x0， y0)． 则AF →＝ p 2 ，－2 ，AM → ＝ y20 2p ，y0－2 . 由已知得，AF → ·AM → ＝0，即 y20－8y0＋16＝0， 因而 y0＝4，M 8 p ，4 . 由 MF＝5，得 8 p －p 2 2＋16＝5， 又 p>0，解得 p＝2 或 p＝8. 故 C 的方程为 y2＝4x 或 y2＝16x.] B 组 能力提升 (建议用时：15 分钟) 1．设 F 为抛物线 C：y2＝3x 的焦点，过 F 且倾斜角为 30°的直线交 C 于 A， B 两点，则 AB＝________. 12 [∵F 为抛物线 C：y2＝3x 的焦点， ∴F 3 4 ，0 ， ∴AB 的方程为 y－0＝tan 30° x－3 4 ，即 y＝ 3 3 x－ 3 4 . 联立 y2＝3x， y＝ 3 3 x－ 3 4 ， 得 1 3x2－7 2x＋ 3 16 ＝0， ∴x1＋x2＝－ －7 2 1 3 ＝21 2 ，即 xA＋xB＝21 2 . 由于 AB＝xA＋xB＋p， ∴AB＝21 2 ＋3 2 ＝12.] 2．(2016·全国卷Ⅰ改编)以抛物线 C 的顶点为圆心的圆交 C 于 A，B 两点， 交 C 的准线于 D，E 两点．已知 AB＝4 2，DE＝2 5，则 C 的焦点到准线的距 离为________． 4 [设抛物线的方程为 y2＝2px(p＞0)，圆的方程为 x2＋y2＝r2. ∵AB＝4 2，DE＝2 5， 抛物线的准线方程为 x＝－p 2 ， ∴不妨设 A 4 p ，2 2 ，D －p 2 ， 5 . ∵点 A 4 p ，2 2 ，D －p 2 ， 5 在圆 x2＋y2＝r2 上， ∴ 16 p2 ＋8＝r2， p2 4 ＋5＝r2， ∴16 p2 ＋8＝p2 4 ＋5，∴p＝4(负值舍去)． ∴C 的焦点到准线的距离为 4.] 3．(2017·南京模拟)如图 503，过抛物线 y2＝2px(p>0)的焦点 F 的直线交抛 物线于点 A，B，交其准线 l 于点 C，若 BC＝2BF，且 AF＝3，则此抛物线的方 程为________． 图 503 y2＝3x [如图，分别过 A，B 作 AA1⊥l 于 A1，BB1⊥l 于 B1，由抛物线的定义知： AF＝AA1，BF＝BB1，∵BC＝2BF，∴BC＝2BB1， ∴∠BCB1＝30°， ∴∠AFx＝60°， 连结 A1F，则△AA1F 为等边三角形，过 F 作 FF1⊥AA1 于 F1，则 F1 为 AA1 的中点，设 l 交 x 轴于 K，则 KF＝A1F1＝1 2AA1＝1 2AF，即 p＝3 2 ，∴抛物线方程为 y2＝3x.] 4．O 为坐标原点，F 为抛物线 C：y2＝4 2x 的焦点，P 为 C 上一点，若 PF ＝4 2，则△POF 的面积为________． 2 3 [如图，设点 P 的坐标为(x0，y0)， 由 PF＝x0＋ 2＝4 2，得 x0＝3 2， 代入抛物线方程得，y20＝4 2×3 2＝24， 所以|y0|＝2 6， 所以 S△POF＝1 2OF|y0|＝1 2 × 2×2 6＝2 3.] 5．(2017·南通调研)已知 P 是抛物线 y2＝4x 上的一个动点，Q 是圆(x－3)2＋ (y－1)2＝1 上的一个动点，N(1,0)是一个定点，则 PQ＋PN 的最小值为________． 3 [由抛物线方程 y2＝4x，可得抛物线的焦点 F(1,0)，又 N(1,0)，所以 N 与 F 重合． 过圆(x－3)2＋(y－1)2＝1 的圆心 M 作抛物线准线的垂线 MH，交圆于 Q，交 抛物线于 P，则 PQ＋PN 的最小值等于 MH－1＝3.] 6．已知一条过点 P(2,1)的直线与抛物线 y2＝2x 交于 A，B 两点，且 P 是弦 AB 的中点，则直线 AB 的方程为________． x－y－1＝0 [依题意，设点 A(x1，y1)，B(x2，y2)，则有 y21＝2x1，y22＝2x2， 两式相减得 y21－y22＝2(x1－x2)，即y1－y2 x1－x2 ＝ 2 y1＋y2 ＝1，直线 AB 的斜率为 1，直线 AB 的方程是 y－1＝x－2，即 x－y－1＝0.]