- 2021-06-12 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全国大联考2019-2020学年高一3月联考试题 数学
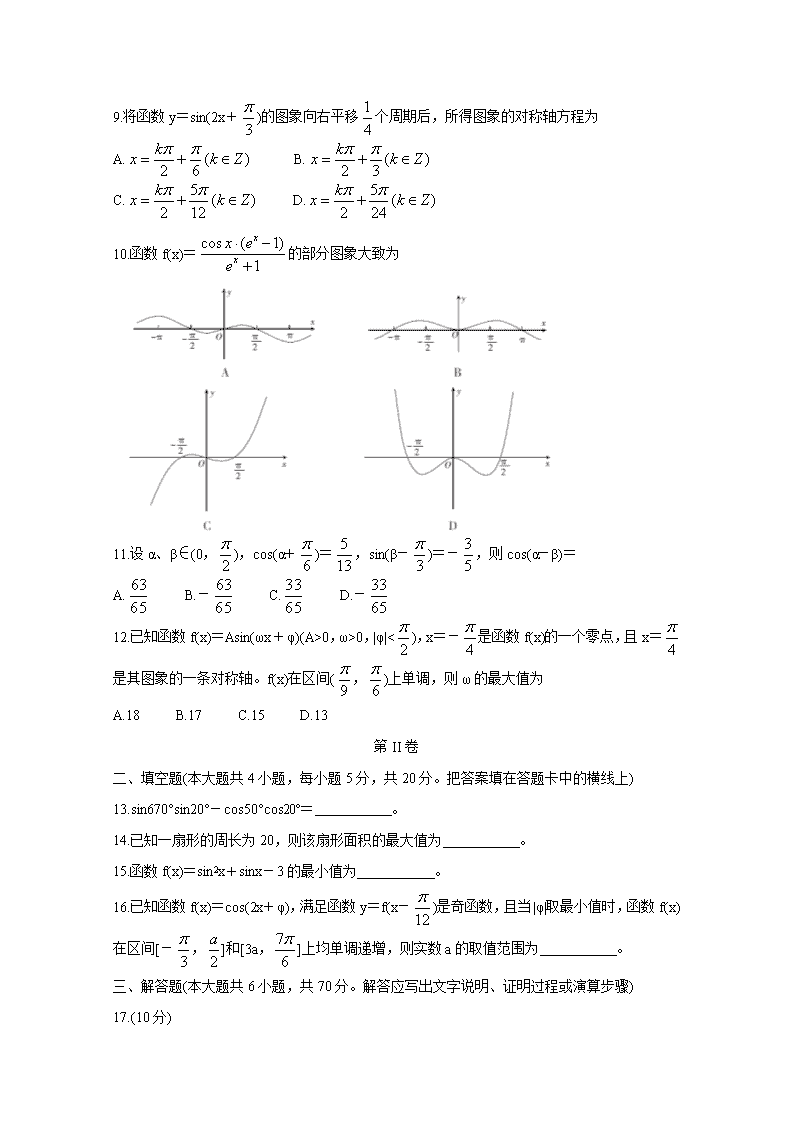
www.ks5u.com 高一数学试卷 考生注意: 1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分。考试时间120分钟。 2.请将各题答案填写在答题卡上。 3.本试卷主要考试内容:人教版必修4第1章和第3章。 第I卷 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知α=,则下列各角中与角α终边相同的是 A. B.- C.- D. 2.已知α的终边上有一点P(-3.4),则sin α= A. B. C.- D.- 3.已知点P(sin α,tan α)在第二象限,则α为 A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 4.下列函数中,既是奇函数,又是周期函数的是 A. y=sin|x| B. y=cos 2x C.y=x3 D. y=cos(+x) 5.要得到函数y=cos(4x+)的图象,只需将函数y= cos(4x+)的图象 A.向左平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移个单位长度 6.已知<α<π,sin(α+)=,则cos2α= A. B.- C. D.- 7.已知函数f(x)=mtanx- ksinx+2(m,k∈R),若f()=1.则f(-)= A.1 B.-1 C.3 D.-3 8.把930°表示成α+ 2kπ(k∈Z)的形式,则|α|的最小值为 A. B. C. D. 9.将函数y=sin(2x+)的图象向右平移个周期后,所得图象的对称轴方程为 A. B. C. D. 10.函数f(x)=的部分图象大致为 11.设α、β∈(0,),cos(α+)=,sin(β-)=-,则cos(α-β)= A. B.- C. D.- 12.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<),x=-是函数f(x)的一个零点,且x=是其图象的一条对称轴。f(x)在区间(,)上单调,则ω的最大值为 A.18 B.17 C.15 D.13 第II卷 二、填空题(本大题共4小题,每小题5分,共20分。把答案填在答题卡中的横线上) 13.sin670°sin20°-cos50°cos20°= 。 14.已知一扇形的周长为20,则该扇形面积的最大值为 。 15.函数f(x)=sin2x+sinx-3的最小值为 。 16.已知函数f(x)=cos(2x+φ),满足函数y=f(x-)是奇函数,且当|φ|取最小值时,函数f(x)在区间[-,]和[3a,]上均单调递增,则实数a的取值范围为 。 三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤) 17.(10分) 已知<α<π,sinα=。 (1)求tanα的值; (2)求4sin2α+sin2α的值。 18.(12分) 已知函数f(x)=4sinxsin(x-)-。 (1)求f(x)的最小正周期; (2)求f(x)在区间[-,]上的值域。 19.(12分) 已知关于x的方程x2+(sinα+cosβ)x-(cosα+sinβ)2=0有两个相等的实数根。 (1)求sin(α+β)的值; (2)若0查看更多