高中数学第7章三角函数课时分层作业31任意角的三角函数含解析苏教版必修第一册

高中数学第7章三角函数课时分层作业31任意角的三角函数含解析苏教版必修第一册

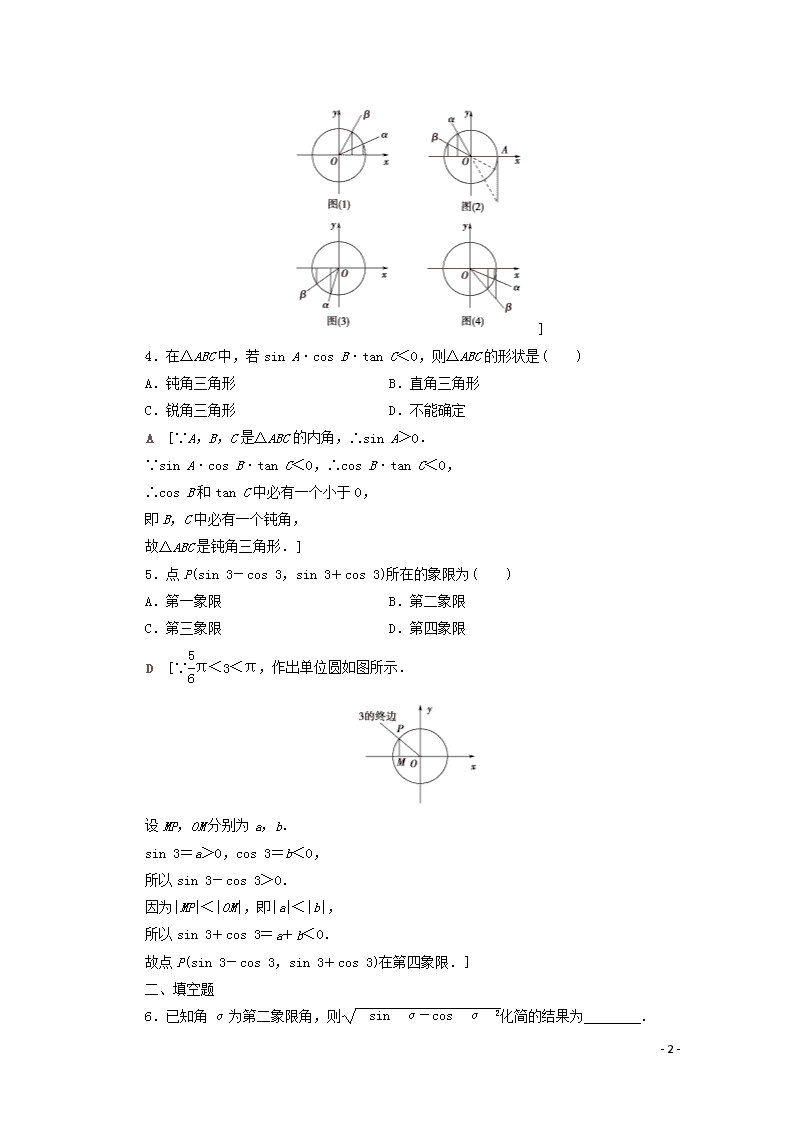
课时分层作业(三十一)　任意角的三角函数 ‎(建议用时：40分钟)‎ 一、选择题 ‎1．已知点P(tan α，cos α)在第三象限，则角α的终边所在象限为(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 B　[由P(tan α，cos α)在第三象限可知tan α<0，cos α<0．‎ 由tan α<0得，角α的终边在第二或第四象限，‎ 由cos α<0得，角α的终边在第二或第三象限或x轴的负半轴．‎ 故角α的终边在第二象限．]‎ ‎2．若角α的终边落在y＝－x上，则tan α的值为(　　)‎ A．－1 B．1‎ C．－1或1 D．不能确定 A　[设P(a，－a)是角α上任意一点，‎ 若a>0，P点在第四象限，tan α＝＝－1，‎ 若a<0，P点在第二象限，tan α＝＝－1．]‎ ‎3．已知cos α＞cos β，那么下列结论成立的是(　　)‎ A．若α，β是第一象限角，则sin α＞sin β B．若α，β是第二象限角，则tan α＞tan β C．若α，β是第三象限角，则sin α＞sin β D．若α，β是第四象限角，则tan α＞tan β D　[由图(1)可知，cos α＞cos β时，sin α＜sin β，A错误；由图(2)可知，cos α＞cos β时，tan α＜tan β，B错误；由图(3)可知，cos α＞cos β时，sin α＜sin β，C错误；由图(4)可知，cos α＞cos β时，tan α＞tan β，D正确．‎ - 6 -‎ ‎]‎ ‎4．在△ABC中，若sin A·cos B·tan C＜0，则△ABC的形状是(　　)‎ A．钝角三角形 B．直角三角形 C．锐角三角形 D．不能确定 A　[∵A，B，C是△ABC的内角，∴sin A＞0．‎ ‎∵sin A·cos B·tan C＜0，∴cos B·tan C＜0，‎ ‎∴cos B和tan C中必有一个小于0，‎ 即B，C中必有一个钝角，‎ 故△ABC是钝角三角形．]‎ ‎5．点P(sin 3－cos 3，sin 3＋cos 3)所在的象限为(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 D　[∵π＜3＜π，作出单位圆如图所示．‎ 设MP，OM分别为a，b．‎ sin 3＝a＞0，cos 3＝b＜0，‎ 所以sin 3－cos 3＞0．‎ 因为|MP|＜|OM|，即|a|＜|b|，‎ 所以sin 3＋cos 3＝a＋b＜0．‎ 故点P(sin 3－cos 3，sin 3＋cos 3)在第四象限．]‎ 二、填空题 ‎6．已知角α为第二象限角，则化简的结果为　　　　．‎ - 6 -‎ sin α－cos α　[因为角α为第二象限角，故sin α>0，cos α<0，因此＝|sin α－cos α|＝sin α－cos α．]‎ ‎7．sin ，cos ，tan 按从小到大的顺序排列是　　　　 ．‎ cos 0，‎ sin >0．‎ ‎∵MP．利用三角函数线，得到α的取值范围是　　　　．‎ ∪　[利用三角函数线得α的终边落在如图所示∠AOB区域内，所以α的取值范围是∪．]‎ ‎5．已知直线y＝x与圆x2＋y2＝1交于A，B两点， 点A在x轴的上方，O是坐标原点．‎ ‎(1)求以射线OA为终边的角α的正弦值和余弦值；‎ - 6 -‎ ‎(2)求以射线OB为终边的角β的正切值．‎ ‎[解]　(1)由 得或 ‎∵点A在x轴上方，‎ ‎∴点A，B的坐标分别为，．‎ ‎∴sin α＝，cos α＝．‎ ‎(2)由(1)得tan β＝＝1．‎ - 6 -‎