- 2021-06-11 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年湖南省衡阳市第八中学高二上学期期中考试数学(理)试题 含部分解析
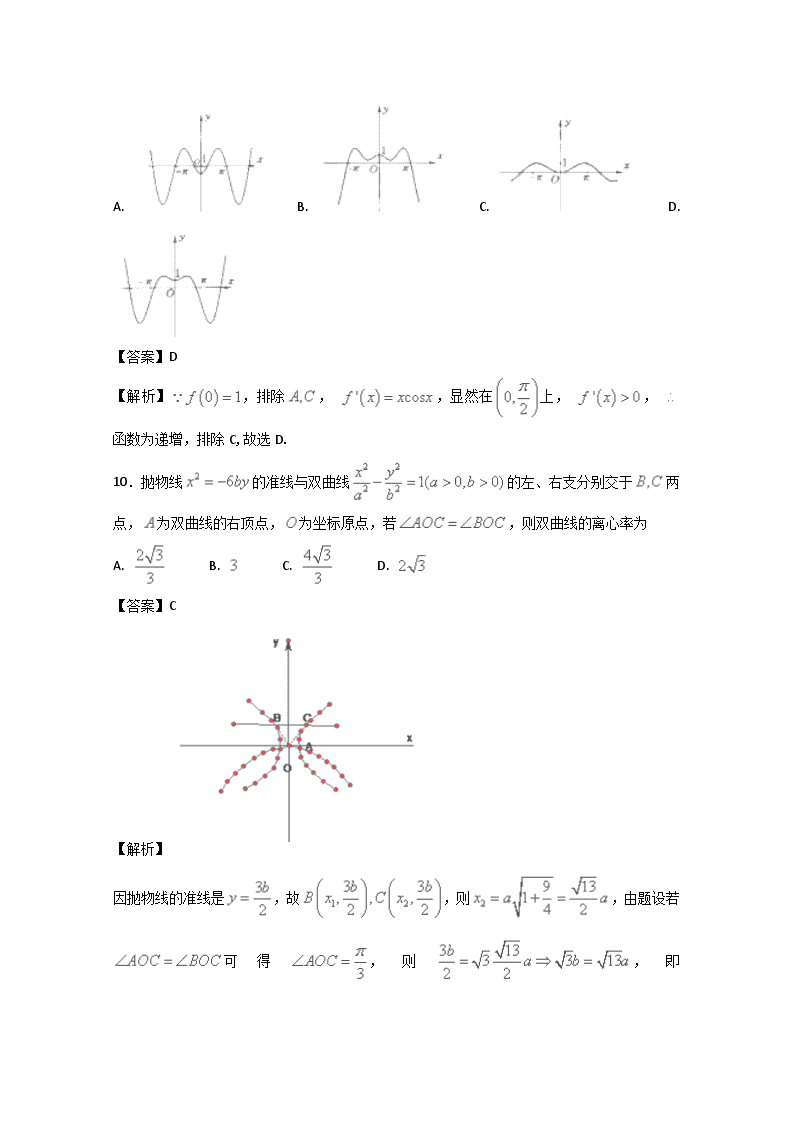
2017-2018学年湖南省衡阳市第八中学高二上学期期中考试数学(理)试题 请注意:时量120分钟 满分100分或120分 特别提示:第?题和第?题为创新班加试试题 (试题、答题卡、答案分做电子版,另所有客观题答案务必做成表格形式放在答案文档的第一行) 一、选择题(本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的) 1.命题“若,则”的逆命题是 A. 若,则 B. 若,则 C. 若,则 D. 若,则 【答案】C 【解析】命题“若,则”的逆命题是“若,则”,所以命题“若,则”的逆命题是若,则,选C. 2.抛物线的准线方程是 A. B. C. D. 【答案】B 【解析】抛物线中,准线. 3.双曲线的渐近线的方程是 A. B. C. D. 【答案】C 【解析】双曲线的渐近线的方程为,故选C。 4.已知向量, ,则“”是“”成立的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】A 【解析】当时, 可以推出, 当时, 不能推出 所以,“”是“”成立的充分不必要条件. 选A. 5. 已知中心在原点的椭圆的右焦点为,离心率等于,则的方程是 A. B. C. D. 【答案】D 6.已知实数构成一个等比数列,则圆锥曲线的离心率为 A. B. C. 或 D. 或 【答案】C 【解析】由已知得,当,则圆锥曲线是椭圆,,离心; 当时则是双曲线,,离心率,故选C. 7.设为曲线:上的点,且曲线在点处切线倾斜角的取值范围为,则点横坐标的取值范围为 A. B. C. D. 【答案】A 8.命题:“”,使,命题:“,是成立的充分条件”,则下列命题为假命题的是 A. B. C. D. 【答案】B 【解析】对恒成立,所以命题p是假命题. 由不等式的乘法性质可知充分性成立. 所以命题q为真命题. 所以B选项错. 选B. 9.函数的图像大致为 A. B. C. D. 【答案】D 【解析】,排除, ,显然在上, , 函数为递增,排除C,故选D. 10.抛物线的准线与双曲线的左、右支分别交于两点,为双曲线的右顶点,为坐标原点,若,则双曲线的离心率为 A. B. C. D. 【答案】C 【解析】 因抛物线的准线是,故,则,由题设若可得,则,即 ,所以,应选答案C。 11.已知椭圆的左、右焦点分别为过作一条直线(不与轴垂直)与椭圆交于两点,如果恰好为等腰直角三角形,该直线的斜率为 A. B. C. D. 【答案】C 【解析】 设,则,,于是,又,所以,所以, ,因此, ,直线斜率为, 由对称性,还有一条直线斜率为,故选C. 12.若实数满足,则的最小值为 A. B. C. D. 【答案】C 考点:利用导数求最值 二、填空题(本大题共4个小题,每小题3分,共12分.把答案填在答题卡中对应题号后的横线上) 13.若抛物线上的点到轴的距离是,则到焦点的距离为 .【答案】10 14.已知函数,其中为实数,为的导函数,若,则的值为 .【答案】3 15. 如图,点分别是正方体的棱和的中点,则和所成角的大小是 .【答案】 16.过抛物线的焦点作直线交抛物线于,两点,若,,则 .【答案】 三、解答题(本大题共52分,解答题应写出必要的文字说明,证明过程或演算步骤) 17.(本小题满分8分)已知且。设:函数在区间内单调递减;:曲线与轴交于不同的两点,如果“”为真命题,“”为假命题 ,求实数的取值范围. 【答案】 试题分析:本题考查复合命题真假判定,考查了指数函数的单调性与曲线的交点问题。根据指数函数在区间内单调递减,可得;曲线与轴交于不同的两点,则,求出或。因为“”为真命题,“”为假命题,所以与恰好一真一假,即可求出实数的取值范围。 试题解析:由“函数在区间内单调递减” 可知:, 由“曲线与轴交于不同的两点” 可知:或, 因为“”为真命题,“”为假命题,所以与恰好一真一假, ①当真,假时,,即. ②当假,真时,,即. 综上可知,的取值范围为:. 18.(本小题满分8分)如图,在四棱锥中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,. (1)求证:PD⊥平面PAB; (2)求直线PB与平面PCD所成角的正弦值. 【答案】(1)见解析;(2). 19.(本小题满分10分)已知双曲线:()的离心率为,虚轴长为. (1)求双曲线的标准方程; (2)过点,倾斜角为的直线与双曲线相交于两点,为坐标原点,求的面积. 【答案】(1);(2). 【解析】(1)依题意可得,解得, ∴双曲线的标准方程为. (2)直线的方程为,设、,由可得, 由韦达定理可得,, 则 原点到直线的距离为,于是, ∴△的面积为. 20.(本小题满分8分)已知函数,求: (1)函数的图象在点处的切线方程; (2)的单调递减区间. 【答案】(1);(2). 21.(本小题满分8分)如图,在四棱锥中,底面,,,点为棱的中点. (1)证明: ; (2)求二面角的余弦值. 【答案】(1)见解析;(2). 试题分析:(1)利用题意首先证明面 然后利用线面垂直的结论可得 . (2)建立空间直角坐标系,由平面的法向量可求得二面角的余弦值为. 试题解析:⑴证明:取中点,连接 分别是的中点 四边形是平行四边形 面 , 面 ⑵以点为坐标原点建立如图所示空间直角坐标系,则 设面的法向量为 由,令,即 面的一个法向量,设二面角的大小为,则 22.(本小题满分10分)已知椭圆: 的长轴长为6,且椭圆与圆: 的公共弦长为. (1)求椭圆的方程. (2)过点作斜率为的直线与椭圆交于,两点,试判断在轴上是否存在点,使得为以为底边的等腰三角形. 若存在,求出点的横坐标的取值范围,若不存在,请说明理由. 【答案】(1);(2)见解析. 试题分析:(1)由长轴长可得值,公共弦长恰为圆直径,可知椭圆经过点,利用待定系数法可得椭圆方程;(2)可令直线的解析式为,设, 的中点为,将直线方程与椭圆方程联立,消去,利用根与系数的关系可得,由等腰三角形中,可得,得出中.由此可得点的横坐标的范围. 试题解析:(1)由题意可得,所以.由椭圆与圆: 的公共弦长为,恰为圆的直径,可得椭圆经过点,所以,解得.所以椭圆的方程为. (2)直线的解析式为,设, 的中点为.假设存在点,使得为以为底边的等腰三角形,则. 由得,故,所以, .因为,所以,即,所以. 当时, ,所以;当时, ,所以. 综上所述,在轴上存在满足题目条件的点,且点的横坐标的取值范围为.查看更多