2020学年高二数学下学期期中试题 理(新版)人教版

2020学年高二数学下学期期中试题 理(新版)人教版

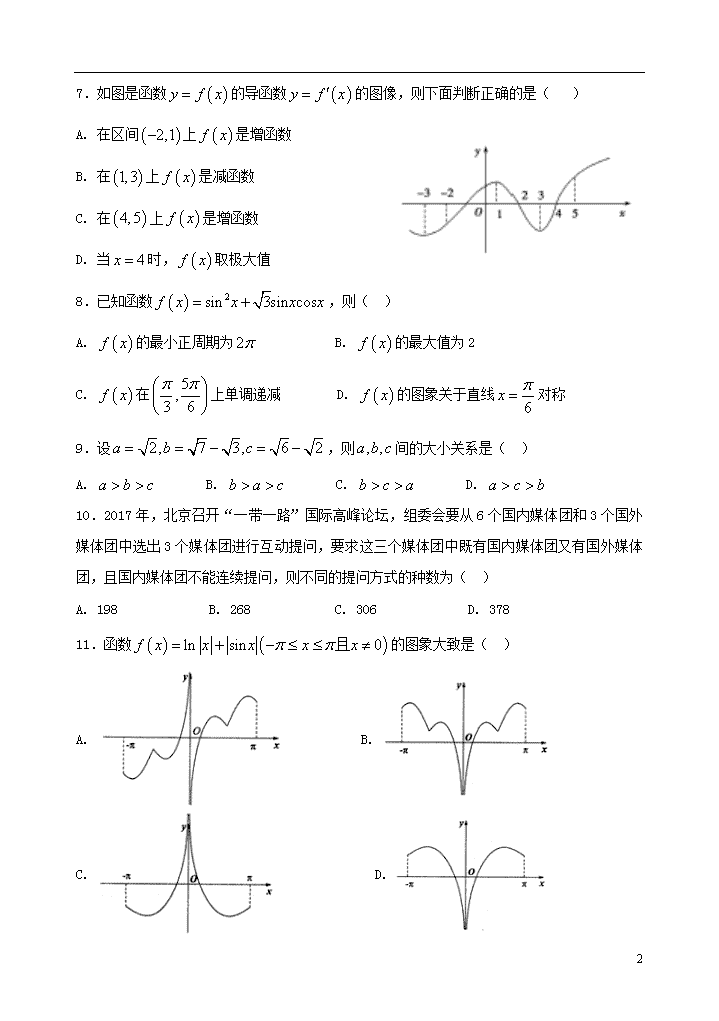
‎2019年春季期中考试卷 高二数学（理科）‎ 考试时间：120分钟 满分：150分 2019.4.28‎ ‎ 班级 座号 姓名 ‎ ‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分，每题只有一个正确选项）‎ ‎1.已知，则复数的共轭复数在复平面内所对应的点位于（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎2．若个人报名参加项体育比赛，每个人限报一项，则不同的报名方法的种数有（ ）‎ A. B. C. D. ‎ ‎3．函数的导函数是（ ）‎ A. B. ‎ C. D. ‎ ‎4．曲线在点处的切线方程为（ ）‎ A. B. C. D. ‎ ‎5．《九章算术》卷5《商功》记载一个问题“今有圆堡瑽，周四丈八尺，高一丈一尺 .问积几何？答曰：二千一百一十二尺.术曰：周自相乘，以高乘之，十二而一”.这里所说的圆堡瑽就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”. 就是说：圆堡瑽（圆柱体）的体积为 (底面圆的周长的平方高)，则由此可推得圆周率的取值为（ ）‎ A. B. C. D. ‎ ‎6．函数在上的最大值和最小值分别是（ ）‎ A. B. C. D. ‎ 21‎ ‎7．如图是函数的导函数的图像，则下面判断正确的是（ ）‎ A. 在区间上是增函数 ‎ B. 在上是减函数 C. 在上是增函数 ‎ D. 当时，取极大值 ‎8．已知函数，则（ ）‎ A. 的最小正周期为 B. 的最大值为2‎ C. 在上单调递减 D. 的图象关于直线对称 ‎9．设，则间的大小关系是（ ）‎ A. B. C. D. ‎ ‎10．2017年，北京召开“一带一路”国际高峰论坛，组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行互动提问，要求这三个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数为（ ）‎ A. 198 B. 268 C. 306 D. 378‎ ‎11．函数的图象大致是（ ）‎ A. B. ‎ C. D. ‎ 21‎ ‎12．设函数 (其中为自然对数的底数，若函数至少存在一个零点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ 第II卷（非选择题 共90分）‎ 二、填空题（本大题共4小题，每题5分，满分20分．）‎ ‎13. 定积分的值为_____.‎ ‎14. 随着中国电子商务的发展和人们对网购的逐渐认识，网购鲜花速递行业迅速兴起．佳佳为祝福母亲的生日，准备在网上定制一束混合花束．客服为佳佳提供了两个系列，如下表：‎ 粉色系列 黄色系列 玫 瑰 戴安娜、粉佳人、糖果、桃红雪山 假日公主、金辉、金香玉 康乃馨 粉色、小桃红、白色粉边 火焰、金毛、黄色 配 叶 红竹蕉、情人草、满天星 散尾叶、栀子叶、黄莺、银叶菊 佳佳要在两个系列中选一个系列，再从中选择2种玫瑰、1种康乃馨、2种配叶组成混合花束．请问佳佳可定制的混合花束一共有________种．‎ ‎15. 2017年吴京执导的动作、军事电影《战狼2》上映三个月，以56.8亿震撼世界的票房成绩圆满收官，该片也是首部跻身全球票房TOP100的中国电影．小明想约甲、乙、丙、丁四位好朋友一同去看《战狼2》，并把标识分别为A,B,C,D的四张电影票放在编号分别为1,2,3,4的四个不同盒子里，让四位好朋友进行猜测：‎ 甲说：第1个盒子里面放的是B，第3个盒子里面放的是C；‎ 乙说：第2个盒子里面放的是B，第3个盒子里面放的是D；‎ 丙说：第4个盒子里面放的是D，第2个盒子里面放的是C；‎ 丁说：第4个盒子里面放的是A，第3个盒子里面放的是C.‎ 小明说：“四位朋友，你们都只说对了一半．”‎ 可以推测，第4个盒子里面放的电影票为___________.‎ 21‎ ‎16．对于函数有以下说法：‎ ‎①是的极值点.‎ ‎②当时， 在上是减函数. ‎ ‎③的图像与处的切线必相交于另一点. ‎ ‎④当时， 在上是减函数.‎ 其中说法正确的序号是_______________.‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17.（本小题满分10分）‎ 复数，满足的虚部是2，Z对应的点在第一象限.‎ ‎（I）求Z；‎ ‎（II）若在复平面上对应点分别为，求.‎ ‎18．（本小题满分12分）‎ 已知函数（），.‎ ‎（I）求曲线在点处的切线方程；‎ ‎（II）若函数，，求的单调区间和最小值.‎ 21‎ ‎19．（本小题满分12分）‎ 如图,在四棱锥中，平面平面，，，，，点在棱上，且.‎ ‎（I）求证：；‎ ‎（II）是否存在实数，使得二面角的余弦值为，若存在，求出实数的值；‎ 若不存在，请说明理由.‎ ‎20．（本小题满分12分）‎ 如图，某地有三家工厂，分别位于矩形ABCD 的顶点A、B 及CD的中点P 处，已知AB=20km,CB =10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域上（含边界），且与A、B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO、BO、OP ，设排污管道的总长度为km．‎ ‎（I）按下列要求写出函数关系式：‎ ①设∠BAO= (rad)，将表示成的函数；‎ ②设OP (km) ，将表示成的函数．‎ ‎（II）请选用（I）中的一个函数关系式，确定污水处理厂的位置，使铺设的排污管道总长度最短．‎ 21‎ ‎21．（本小题满分12分）‎ 已知椭圆方程为，它的一个顶点为，离心率.‎ ‎（I）求椭圆的方程；‎ ‎（II）设直线与椭圆交于， 两点，坐标原点到直线的距离为，求面积的最大值.‎ ‎22．（本小题满分12分）‎ 已知， ．‎ ‎（I）讨论的单调性；‎ ‎（II）若，求实数的取值范围．‎ ‎2019年春季期中考试卷 高二数学（理科）参考答案 ‎ 考试时间：120分钟 满分：150分 2019.4.28‎ ‎ 班级 座号 姓名 ‎ ‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分，每题只有一个正确选项）‎ 21‎ ‎1.已知，则复数的共轭复数在复平面内所对应的点位于（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎【答案】D ‎【解析】由题意， ，对应点为，在第四象限，故选D.‎ ‎2．若个人报名参加项体育比赛，每个人限报一项，则不同的报名方法的种数有（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】四名同学报名参加3项体育比赛，每人限报一项，每人有3种报名方法；根据分步计数原理，可得共有3×3×3×3=种不同的报名方法，故选C.‎ ‎3．函数的导函数是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】＝，故选D．‎ 考点：导数的计算．‎ ‎4．曲线在点处的切线方程为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由函数的解析式有： ，‎ 由题意可得： ，‎ 则函数在点处的切线的斜率为： ，‎ 据此可得曲线在点处的切线方程为，‎ 21‎ 即.‎ ‎5．《九章算术》卷5《商功》记载一个问题“今有圆堡瑽，周四丈八尺，高一丈一尺 .问积几何？答曰：二千一百一十二尺.术曰：周自相乘，以高乘之，十二而一”.这里所说的圆堡瑽就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”. 就是说：圆堡瑽（圆柱体）的体积为 (底面圆的周长的平方高)，则由此可推得圆周率的取值为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】设圆柱体的底面半径为，高为，由圆柱的体积公式得体积为： .‎ 由题意知.‎ 所以，解得.‎ 故选A.‎ ‎6．函数在上的最大值和最小值分别是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由题设知y′=6x2−6x−12，‎ 令y′>0，解得x>2，或x<−1，‎ 故函数y=2x3−3x2−12x+5在[0,2]上减,在[2,3]上增，‎ 当x=0，y=5；当x=3，y=−4；当x=2，y=−15.‎ 由此得函数y=2x3−3x2−12x+5在[0,3]上的最大值和最小值分别是5，−15；‎ 故选B.‎ ‎7．如图是函数的导函数的图像，则下面判断正确的是（ ）‎ A. 在区间上是增函数 ‎ B. 在上是减函数 C. 在上是增函数 ‎ D. 当时，取极大值 21‎ ‎【答案】C ‎【解析】根据原函数与导函数的关系，由导函数的图象可知的单调性如下： 在上为减函数，在（0,2）上为增函数，在（2,4）上为减函数，在（4,5）上为增函数，在的左侧为负，右侧为正，故在处取极小值，结合选项，只有选项C正确。‎ ‎8．已知函数，则（ ）‎ A. 的最小正周期为 B. 的最大值为2‎ C. 在上单调递减 D. 的图象关于直线对称 ‎【答案】C ‎【解析】∵函数 ‎∴的最小正周期为，故错误 的最大值为，故错误 当时， ，故的图象不关于直线对称，故错误 由，得，令，可得的一个单调减区间为，故C正确 ‎9．设，则间的大小关系是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】∵， ， ‎ 21‎ ‎， ，‎ ‎∴ ，故选D.‎ ‎10．2017年，北京召开“一带一路”国际高峰论坛，组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行互动提问，要求这三个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数为（ ）‎ A. 198 B. 268 C. 306 D. 378‎ ‎【答案】A ‎【解析】分两种情况，若选两个国内媒体一个国外媒体，有 种不同提问方式；若选两个外国媒体一个国内媒体，有种不同提问方式，所以共有种提问方式，故选A. ‎ ‎11．函数的图象大致是（ ）‎ A. B. ‎ C. D. ‎ ‎【解析】函数是偶函数排除A.‎ 当时, ,可得： ,令，‎ 作出 与 图象如图：可知两个函数有一个交点，就是函数有一个极值点， ‎ 21‎ 故选：D.‎ ‎12．设函数 (其中为自然对数的底数，若函数至少存在一个零点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】令,则，‎ 设，令， ，‎ ‎∴，发现函数在上都是单调递增，在上都是单调递减，‎ ‎∴函数在上单调递增，在上单调递减，故当时，得，‎ ‎∴函数至少存在一个零点需满足，即.选D.‎ 第II卷（非选择题 共90分）‎ 21‎ 二、填空题（本大题共4小题，每题5分，满分20分．）‎ ‎13. 定积分的值为_____.‎ ‎【答案】‎ ‎【解析】 ‎ 故答案为.‎ ‎14. 随着中国电子商务的发展和人们对网购的逐渐认识，网购鲜花速递行业迅速兴起．佳佳为祝福母亲的生日，准备在网上定制一束混合花束．客服为佳佳提供了两个系列，如下表：‎ 粉色系列 黄色系列 玫 瑰 戴安娜、粉佳人、糖果、桃红雪山 假日公主、金辉、金香玉 康乃馨 粉色、小桃红、白色粉边 火焰、金毛、黄色 配 叶 红竹蕉、情人草、满天星 散尾叶、栀子叶、黄莺、银叶菊 佳佳要在两个系列中选一个系列，再从中选择2种玫瑰、1种康乃馨、2种配叶组成混合花束．请问佳佳可定制的混合花束一共有________种．‎ ‎【答案】108‎ ‎【解析】若选粉色系列有 种选法，若选黄色系列有 种选法，佳佳可定制的混合花束一共有 种.‎ ‎15. 2017年吴京执导的动作、军事电影《战狼2》上映三个月，以56.8亿震撼世界的票房成绩圆满收官，该片也是首部跻身全球票房TOP100的中国电影．小明想约甲、乙、丙、丁四位好朋友一同去看《战狼2》，并把标识分别为A,B,C,D的四张电影票放在编号分别为1,2,3,4的四个不同盒子里，让四位好朋友进行猜测：‎ 甲说：第1个盒子里面放的是B，第3个盒子里面放的是C；‎ 21‎ 乙说：第2个盒子里面放的是B，第3个盒子里面放的是D；‎ 丙说：第4个盒子里面放的是D，第2个盒子里面放的是C；‎ 丁说：第4个盒子里面放的是A，第3个盒子里面放的是C.‎ 小明说：“四位朋友，你们都只说对了一半．”‎ 可以推测，第4个盒子里面放的电影票为___________.‎ ‎【答案】A或D ‎【解析】因为四个人都只猜对了一半，故有以下两种可能：①当甲猜对第1个盒子里面放的是B时，第3个盒子里面放的不是C，则丁猜对第4个盒子里面放的是A，丙猜对第2个盒子里面放的是C，乙猜对第3个盒子里面放的是D；②若甲猜对第3个盒子里面放的是C，则乙猜对第2个盒子里面放的是B，丙猜对第4个盒子里面放的是D，故丁猜对第3个盒子里面放的是C，综上，第4个盒子里面放的电影票为A或D，故答案为或.‎ ‎16．对于函数有以下说法：‎ ‎①是的极值点.‎ ‎②当时， 在上是减函数. ‎ ‎③的图像与处的切线必相交于另一点. ‎ ‎④当时， 在上是减函数.‎ 其中说法正确的序号是_______________.‎ ‎【答案】②③‎ ‎【解析】由于函数,则 ‎①由于在恒为正或恒为负,故x=0不是f(x)的极值点，故①错误；‎ ‎②由于a<0时, <0在(−∞,+∞)上恒成立,则f(x)在(−∞,+∞)上是减函数，故②正确；‎ ‎③由于,则f′(1)=3a 故f(x)在(1,f(1))处的切线方程：y−a=3a(x−1)，即：y=3ax−2a，‎ 联立y=a,(a≠0)得到a=3ax−2a,整理得=0，即或2， 的图像与处的切线,故③正确；‎ 21‎ ‎④当时， 在(−∞,+∞)上恒成立, 在上是增函数函数,故④错误.‎ 故答案为②③.‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17.（本小题满分10分）‎ 复数，满足的虚部是2，Z对应的点在第一象限.‎ ‎（I）求Z；‎ ‎（II）若在复平面上对应点分别为，求.‎ ‎（1）依题意得，结合x>0,y>0知，x=1,y=1‎ ‎（2）由（1）值z=1+i, , ‎ 所以A（1,1），B（0,2），C（1，-1）‎ 有AB=，AC=2，BC= ‎ 由余弦定理可得cos∠ABC=‎ ‎18．（本小题满分12分）‎ 已知函数（），.‎ ‎（I）求曲线在点处的切线方程；‎ ‎（II）若函数，，求的单调区间和最小值.‎ 21‎ ‎（1）因为，‎ 由即，得，‎ 则的解析式为，即有， ‎ 所以所求切线方程为.‎ ‎（2）∵，∴，‎ 由，得或，‎ 由，得，‎ ‎∵，‎ ‎∴的单调增区间为，减区间为，‎ ‎∵，‎ ‎∴的最小值为.‎ ‎19．（本小题满分12分）‎ 如图,在四棱锥中，平面平面，，，，，点在棱上，且.‎ ‎（I）求证：；‎ ‎（II）是否存在实数，使得二面角的余弦值为，若存在，求出实数的值；‎ 若不存在，请说明理由.‎ 解析：（Ⅰ）过点作交于，‎ 21‎ ‎，，‎ 四边形为正方形，且，‎ 在中，，在中， ‎ ‎  ‎ 又平面平面，平面平面 平面   ‎ 平面，且 平面                   ‎ ‎（Ⅱ） ‎ 又平面平面，平面平面 平面 ，          ‎ 以点为坐标原点，、、所在直线为坐标轴建立空间直角坐标系，‎ 假设存在实数使得二面角的余弦值为，令 点在棱上，‎ 设 则，‎ 平面，平面的一个法向量为   ‎ 设平面的一个法向量为 由得令得 取                             ‎ 21‎ 化简得又                ‎ 存在实数使得二面角的余弦值为.‎ ‎20．（本小题满分12分）‎ 如图，某地有三家工厂，分别位于矩形ABCD 的顶点A、B 及CD的中点P 处，已知AB=20km,CB =10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域上（含边界），且与A、B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO、BO、OP ，设排污管道的总长度为km．‎ ‎（I）按下列要求写出函数关系式：‎ ①设∠BAO= (rad)，将表示成的函数；‎ ②设OP (km) ，将表示成的函数．‎ ‎（II）请选用（I）中的一个函数关系式，确定污水处理厂的位置，使铺设的排污管道总长度最短．‎ 试题解析：‎ ‎（1）①由条件知PQ 垂直平分AB，若∠BAO= (rad) ，‎ 则, 故，又OP＝，‎ 所以， ‎ 所求函数关系式为 ‎ 21‎ ‎②若OP= (km) ，则OQ＝10－，‎ 所以OA =OB=‎ 所求函数关系式为 ‎（2）选择函数模型①，‎ 令0 得sin ，因为，所以=，‎ 当时， ， 是的减函数；当时， ， 是的增函 数，所以函数在=时取得极小值，这个极小值就是最小值． ．这时 (km)‎ 因此，当污水处理厂建在矩形区域内且到A、B的距离均为 (km)时，铺设的排污管道总长度最短．‎ ‎21．（本小题满分12分）‎ 已知椭圆方程为，它的一个顶点为，离心率.‎ ‎（I）求椭圆的方程；‎ ‎（II）设直线与椭圆交于， 两点，坐标原点到直线的距离为，求面积的最大值.‎ 21‎ ‎（1）设，‎ 依题意得解得∴椭圆的方程为.‎ ‎（2）①当轴时， .‎ ‎②当与轴不垂直时，设直线的方程为，‎ 由已知，得，把代入椭圆方程，整理得，‎ ‎∴.‎ ‎∴，‎ ‎ ‎ ‎.‎ 当且仅当，即时等号成立，此时.③当时， .综上所述：‎ ‎，此时面积取最大值.‎ 21‎ ‎22．（本小题满分12分）‎ 已知， ．‎ ‎（I）讨论的单调性；‎ ‎（II）若，求实数的取值范围．‎ 试题解析：（1） ， ‎ 当时， ， ．∴在上单调递增； ‎ 当时，由，得．‎ 当时， ；当时， ．‎ 所以在单调递减；在单调递增． ‎ ‎（2）令，‎ 问题转化为在上恒成立，‎ ‎，注意到． ‎ 当时， ，‎ ‎，‎ 因为，所以， ，‎ 所以存在，使，‎ 当时， ， 递减，‎ 所以，不满足题意． ‎ 当时， ，‎ 因为， ， ，‎ 21‎ 所以， 在上单调递增；所以，满足题意．‎ 综上所述： ．‎ 21‎