【数学】宁夏青铜峡市高级中学（吴忠中学青铜峡分校）2019-2020学年高二下学期期中考试（理）

【数学】宁夏青铜峡市高级中学（吴忠中学青铜峡分校）2019-2020学年高二下学期期中考试（理）

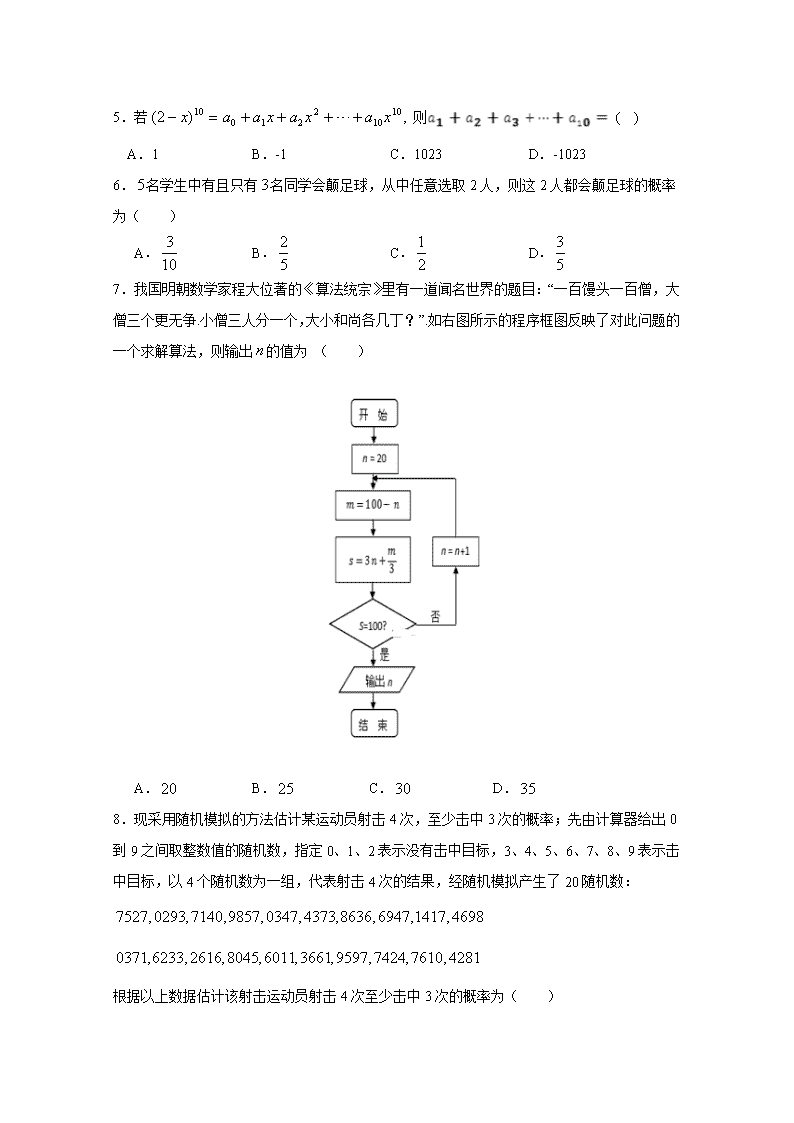
宁夏青铜峡市高级中学（吴忠中学青铜峡分校）2019-2020‎ 学年高二下学期期中考试（理）‎ 一、选择题（本大题共12个小题，每小题5分，共60分）‎ ‎1.某校的书法绘画，乐器演奏，武术爱好三个兴趣小组的人数分别为600，400，300，若用分层抽样方法抽取n名学生参加某项活动，已知从武术小组中抽取了6名学生，则n的值为（ ）‎ A．20 B．22 C．23 D．26‎ ‎2．某校8位学生的本次月考成绩恰好都比上一次的月考成绩高出50分，则以该8位学生这两次的月考成绩各自组成样本，则这两个样本不变的数字特征是（ ）‎ A．方差 B．中位数 C．众数 D．平均数 ‎3．某学校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5,25），[25，27.5），[27.5，30].根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（ ）‎ A．56 B．60 C．140 D．120‎ ‎4．某公司从、两个部门中各选出6名员工参加本季度的笔试考核，他们取得的成绩（满分100分）的茎叶图如图，其中部门员工成绩的中位数是83，部门员工成绩的平均数是85，则的值为（ ）‎ A．2 B．3 C．4 D．5‎ ‎5．若, 则( )‎ A．1 B．-1 C．1023 D．-1023‎ ‎6．名学生中有且只有名同学会颠足球，从中任意选取2人，则这2人都会颠足球的概率为（ ）‎ A． B． C． D．‎ ‎7．我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争.小僧三人分一个，大小和尚各几丁？”.如右图所示的程序框图反映了对此问题的一个求解算法，则输出的值为 （ ）‎ A． B． C． D．‎ ‎8．现采用随机模拟的方法估计某运动员射击4次，至少击中3次的概率；先由计算器给出0到9之间取整数值的随机数，指定0、1、2表示没有击中目标，3、4、5、6、7、8、9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了20随机数：‎ 根据以上数据估计该射击运动员射击4次至少击中3次的概率为（ ）‎ A．0.55 B．0.6 C．0.65 D．0.7‎ ‎9．在高三下学期初，某校开展教师对学生的家庭学习问卷调查活动，已知现有3名教师对4名学生家庭问卷调查，若这3名教师每位至少到一名学生家中问卷调查，又这4名学生的家庭都能且只能得到一名教师的问卷调查，那么不同的问卷调查方案的种数为（ ）‎ A．72 B．48 C．36 D．24‎ ‎10．函数的大致图象是（ ）‎ A． B． C． D．‎ ‎11．若函数恰有3个零点，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎12．若函数在是增函数，则的最大值是（ ）‎ A． B． C． D．‎ 二、填空题（本大题共4个小题，每小题5分，共20分）‎ ‎13．某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:)之间的关系如下:‎ x ‎0‎ ‎1‎ ‎2‎ y ‎5‎ m ‎2‎ ‎2‎ ‎1‎ 通过上面的五组数据得到了x与y之间的线性回归方程:； 但现在丢失了一个数据m，该数据m应为____________‎ ‎14.已知函数,, 则=     ．‎ ‎15．某兴趣小组有2名女生和3名男生，现从中任选2名学生去参加活动，则至多有一名男生的概率为_____________.‎ ‎16．的展开式中，含的项的系数为_____.（用数字填写答案）‎ 三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．‎ ‎17．(本题10分) 设x＝1与x＝2是函数f(x)＝aln x＋bx2＋x的两个极值点．‎ ‎(1)试确定常数a和b的值；‎ ‎(2)判断x＝1，x＝2是函数f(x)的极大值点还是极小值点，并说明理由．‎ ‎18．(本题12分) 选修4-4: 参数方程与极坐标 ‎ 在直角坐标系中，圆的参数方程为（为参数），在以坐标原点为极点，轴非负半轴为极轴建立的极坐标系中，直线的极坐标方程为．‎ ‎（1）求圆的普通方程和直线的直角坐标方程；‎ ‎（2）设点是圆上任一点，求点到直线距离的最小值．‎ ‎19．(本题12分) 选修4-5：不等式选讲 已知函数．‎ ‎（1）求不等式的解集；‎ ‎（2）若的最小值为，求的最小值，并指出此时的值．‎ ‎20．(本题12分) 某地区某农产品近几年的产量统计如表：‎ 年份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 年份代码 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 年产量（万吨）‎ ‎6.6‎ ‎6.7‎ ‎7‎ ‎7.1‎ ‎7.2‎ ‎7.4‎ ‎（I）根据表中数据，建立关于的线性回归方程；‎ ‎（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量．‎ 附：对于一组数据， ，…， ，其回归直线的斜率和截距的最小二乘估计分别为：．‎ ‎（参考数据：，计算结果保留小数点后两位）‎ ‎21．(本题12分) 某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成，，，，，六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题：‎ ‎（1）求分数内的频率，并补全这个频率分布直方图；‎ ‎（2）从频率分布直方图中，估计本次考试成绩的中位数；‎ ‎（3）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率.‎ ‎22．(本题12分) 设函数，，，记.‎ ‎（1）求曲线在处的切线方程；‎ ‎（2）求函数的单调区间；‎ ‎（3）当时，若函数没有零点，求的取值范围.‎ 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D A C A D A B B C A B A ‎13． 4 14． 0 15． 16． 35‎ ‎17． (1)∵f(x)＝aln x＋bx2＋x，∴f′(x)＝＋2bx＋1.‎ 由极值点的必要条件可知：f′(1)＝f′(2)＝0，‎ ‎∴a＋2b＋1＝0且＋4b＋1＝0，解方程组得，a＝ ，b＝ .‎ ‎(2)由(1)可知f(x)＝ln xx2＋x，‎ 且函数f(x)＝ln xx2＋x的定义域是(0，＋∞)，‎ f′(x)＝x－1x＋1＝ .‎ 当x∈(0,1)时，f′(x)＜0；当x∈(1,2)时，f′(x)＞0；当x∈(2，＋∞)时，f′(x)＜0；‎ 所以，x＝1是函数f(x)的极小值点， x＝2是函数f(x)的极大值点．‎ ‎18．（1）由消去参数，得，‎ 所以圆的普通方程为．‎ 由，得，‎ 所以直线的直角坐标方程为．‎ ‎（2）设点的坐标为，‎ 则点到直线的距离为，‎ 当时，取最小值，．‎ ‎19．（1）原不等式等价于分别解得，综上所述，不等式的解集为. ‎ ‎（2）依题意，可知，‎ ‎20．（1）由题意可知：，‎ ‎， ‎ ‎，‎ ‎∴，‎ 又， ‎ ‎∴y关于t的线性回归方程为． ‎ ‎（2）由（1）可得，当年份为2019年时，年份代码，此时，‎ 所以，可预测2019年该地区该农产品的年产量约为万吨．‎ ‎21．（1）设分数在内的频率为，根据频率分布直方图，‎ 则有，可得，‎ 所以频率分布直方图为：‎ ‎（2）以中位数为准做一条垂直于横轴的直线，这条直线把频率分布直方图分成面积相等的两个部分，由频率分布直方图知中位数要把最高的小长方形三等分，‎ 所以中位数是，所以估计本次考试成绩的中位数为 ‎（3）设所抽取2人成绩之差的绝对值大于10为事件，‎ 第1组学生数：人（设为1，2，3，4，5，6）‎ 第6组学生数：人（设为）‎ 所有基本事件有：12，13，14，15，16，，23，24，25，26，，，，34，35，36，，，，45，46，，,，56，，，，，，，，，共有35种，‎ 事件包括的基本事件有：，，，，，，，，,，，，，，，共有18种 所以. ‎ ‎22．(1)，则函数在处的切线的斜率为.又，‎ 所以函数在处的切线方程为,即 ‎ ‎（2），，（）.‎ ‎①当时，，在区间上单调递增；‎ ‎②当时，令，解得；令，解得.‎ 综上所述，当时，函数的增区间是；‎ 当时，函数的增区间是，减区间是. ‎ ‎（3）依题意，函数没有零点，即无解.‎ 由（2）知，当时，函数在区间上为增函数,区间上为减函数，‎ 由于，只需，‎ 解得.所以实数的取值范围为.‎