2017届高考文科数学(全国通用)二轮适考素能特训:专题3-3-2中档题专练
二、中档题专练
(一)
1.[2016·长春监测]已知函数f(x)=2sinxcosx+2cos2x-.
(1)求函数y=f(x)的最小正周期和单调递减区间;
(2)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f=,且sinB+sinC=,求△ABC的面积.
解 (1)f(x)=2sinxcosx+2cos2x-=sin2x+cos2x=2sin,
因此f(x)的最小正周期为T==π.
f(x)的单调递减区间为2kπ+≤2x+≤2kπ+(k∈Z),
即x∈(k∈Z).
(2)由f=2sin=2sinA=,又A为锐角,所以A=.
由正弦定理可得2R===,
sinB+sinC==,
则b+c=×=13,由余弦定理可知,cosA===,可求得bc=40,
故S△ABC=bcsinA=10.
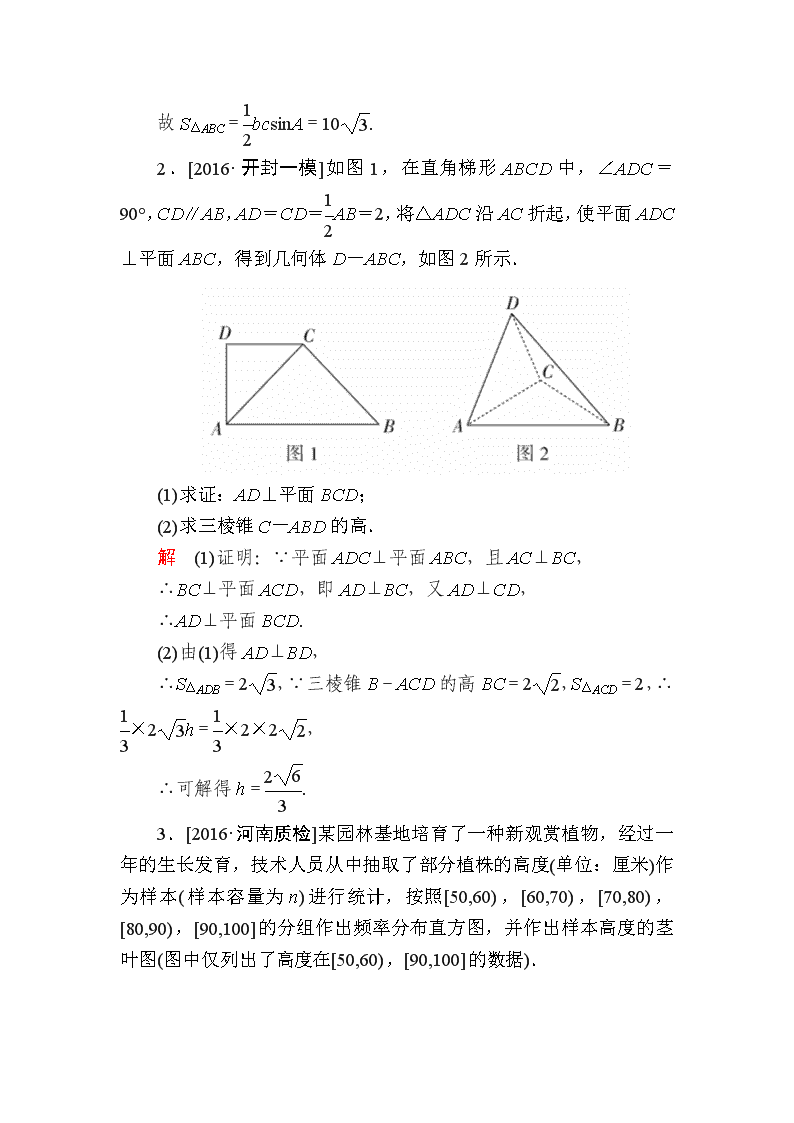
2.[2016·开封一模]如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
(1)求证:AD⊥平面BCD;
(2)求三棱锥C-ABD的高.
解 (1)证明:∵平面ADC⊥平面ABC,且AC⊥BC,
∴BC⊥平面ACD,即AD⊥BC,又AD⊥CD,
∴AD⊥平面BCD.
(2)由(1)得AD⊥BD,
∴S△ADB=2,∵三棱锥B-ACD的高BC=2,S△ACD=2,∴×2h=×2×2,
∴可解得h=.
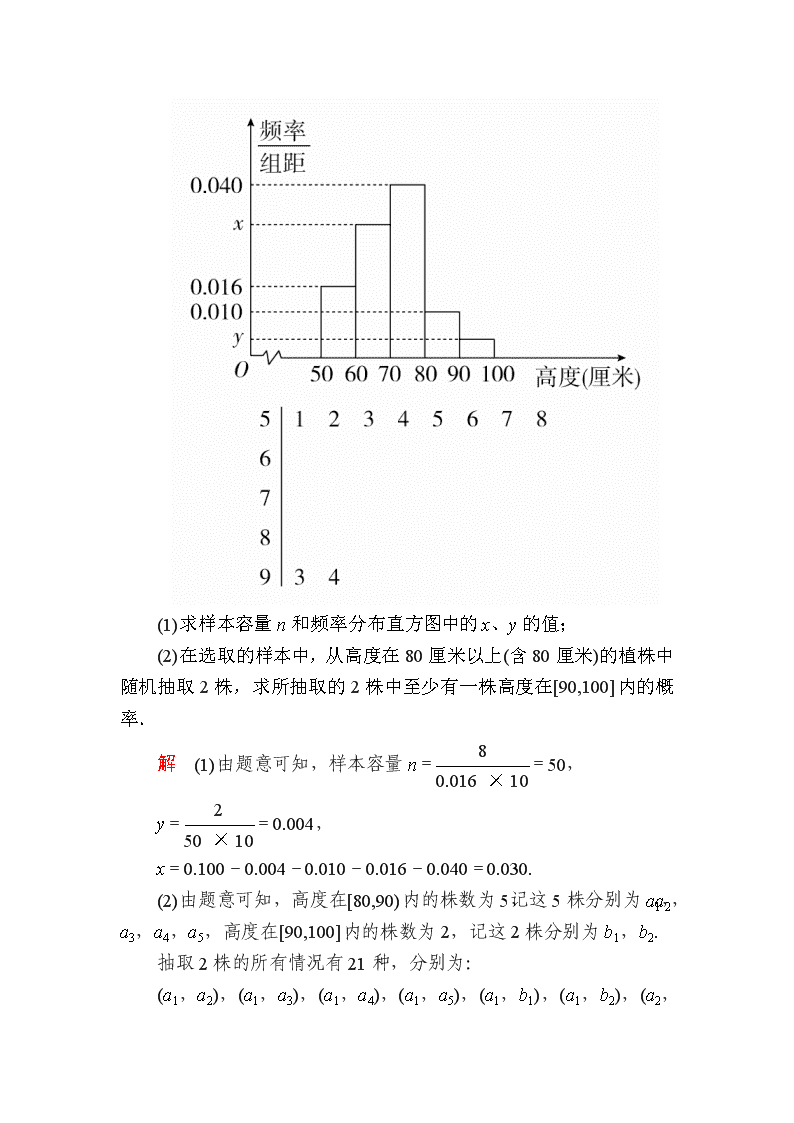
3.[2016·河南质检]某园林基地培育了一种新观赏植物,经过一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在[50,60),[90,100]的数据).
(1)求样本容量n和频率分布直方图中的x、y的值;
(2)在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取2株,求所抽取的2株中至少有一株高度在[90,100]内的概率.
解 (1)由题意可知,样本容量n==50,
y==0.004,
x=0.100-0.004-0.010-0.016-0.040=0.030.
(2)由题意可知,高度在[80,90)内的株数为5,记这5株分别为a1,a2,a3,a4,a5,高度在[90,100]内的株数为2,记这2株分别为b1,b2.
抽取2株的所有情况有21种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2).
其中2株的高度都不在[90,100]内的情况有10种,分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2株中至少有一株高度在[90,100]内的概率P=1-=.
(二)
1.[2016·云南统检]设数列{an}的前n项和为Sn,对任意正整数n,3an-2Sn=2.
(1)求数列{an}的通项公式;
(2)求证:Sn+2Sn
0,故q=2,从而an==22n-1,即数列{an}的通项公式为an=22n-1.
(2)由(1)知a1=2,数列{an}是以22为公比的等比数列,
故Sn==(22n-1).
因此不等式Sk≥30(2k+1)可化为(22k-1)≥30(2k+1),
即(2k-1)(2k+1)≥30(2k+1),
因为2k+1>0,所以2k≥46,即k≥log246.
又510.828,
所以能在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关.
(2)设其他学生为丙和丁,4人分组的情况如下表:
小组
1
2
3
4
5
6
收集成绩
甲乙
甲丙
甲丁
乙丙
乙丁
丙丁
数据处理
丙丁
乙丁
乙丙
甲丁
甲丙
甲乙
分组的情况总共有6种,学生甲负责收集成绩且学生乙负责数据处理占2种,
所以学生甲负责收集成绩且学生乙负责数据处理的概率P==.
3.[2016·广州模拟]在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
(1)当CF=2时,证明:B1F⊥平面ADF;
(2)若FD⊥B1D,求三棱锥B1-ADF的体积.
解 (1)证明:因为AB=AC,D是BC的中点,
所以AD⊥BC.
在直三棱柱ABC-A1B1C1中,
因为B1B⊥底面ABC,AD⊂底面ABC,
所以AD⊥B1B.
因为BC∩B1B=B,
所以AD⊥平面B1BCC1.
因为B1F⊂平面B1BCC1,
所以AD⊥B1F.
在矩形B1BCC1中,因为C1F=CD=1,B1C1=CF=2,
所以Rt△DCF≌Rt△FC1B1,
所以∠CFD=∠C1B1F,所以∠B1FD=90°.
(或通过计算FD=B1F=,B1D=,得到△B1FD为直角三角形)
所以B1F⊥FD.
因为AD∩FD=D,
所以B1F⊥平面ADF.
(2)由(1)可得AD⊥平面B1DF,AD=2,
因为D是BC的中点,所以CD=1.
在Rt△B1BD中,BD=CD=1,BB1=3,
所以B1D==.
因为FD⊥B1D,所以Rt△CDF∽Rt△BB1D,
所以=,所以DF=×=,
所以VB1-ADF=S△B1DF·AD=××××2=.
(四)
1.[2016·贵州八校联考]在△ABC中,角A,B,C的对边分别为a,b,c,向量m=(a+b,sinA-sinC),向量n=(c,sinA-sinB),且m∥n.
(1)求角B的大小;
(2)设BC中点为D,且AD=,求a+2c的最大值及此时△ABC的面积.
解 (1)因为m∥n,故有(a+b)(sinA-sinB)-c(sinA-sinC)=0
由正弦定理可得(a+b)(a-b)-c(a-c)=0,即a2+c2-b2=ac,
由余弦定理可知cosB===,因为B∈(0,π),所以B=.
(2)设∠BAD=θ,则在△BAD中,
由B=可知θ∈,
由正弦定理及AD=有===2;
所以BD=2sinθ,AB=2sin=cosθ+sinθ,
所以a=2BD=4sinθ,c=AB=cosθ+sinθ,
从而a+2c=2cosθ+6sinθ=4sin,
由θ∈可知θ+∈,所以当θ+=,
即θ=时,a+2c的最大值为4;
此时a=2,c=,所以S=acsinB=.
2.如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
(1)求证:AC⊥平面BCE;
(2)求三棱锥E-BCF的体积.
解 (1)证明:过点C作CM⊥AB,垂足为M,因为AD⊥DC,所以四边形ADCM为矩形,所以AM=MB=2,
又AD=2,AB=4,所以AC=2,CM=2,BC=2,
所以AC2+BC2=AB2,所以AC⊥BC,因为AF⊥平面ABCD,AF∥BE,
所以BE⊥平面ABCD,所以BE⊥AC.
又BE⊂平面BCE,BC⊂平面BCE,且BE∩BC=B,
所以AC⊥平面BCE.
(2)因为AF⊥平面ABCD,所以AF⊥CM,
又CM⊥AB,AF⊂平面ABEF,
AB⊂平面ABEF,AF∩AB=A,所以CM⊥平面ABEF.
VE-BCF=VC-BEF=××BE×EF×CM=×2×4×2=.
3.电影《功夫熊猫3》预计在2016年1月29日上映.某地电影院为了了解当地影迷对票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
x(单位:元)
30
40
50
60
y(单位:万人)
4.5
4
3
2.5
(1)若y与x具有较强的相关关系,试分析y与x之间是正相关还是负相关;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)根据(2)中求出的线性回归方程,预测票价定为多少元时,能获得最大票房收入.
参考公式:=,=-.
解 (1)由表中数据易知,y随x的增大而减小,故y与x之间是负相关.
(2)由表中数据可得=45,=3.5,
xiyi-4 =-35,x-42=500,
则==-0.07,=3.5+0.07×45=6.65,
所以,所求线性回归方程为=-0.07x+6.65.
(3)根据(2)中的线性回归方程,若票价为x元,则渴望观影人数为(-0.07x+6.65)万人,
可预测票房收入为z=x(-0.07x+6.65)=-0.07x2+6.65x,
易得,当x=47.5时,z取得最大值,即票价定为47.5元时,能获得最大票房收入.