- 2021-06-11 发布 |
- 37.5 KB |
- 9页

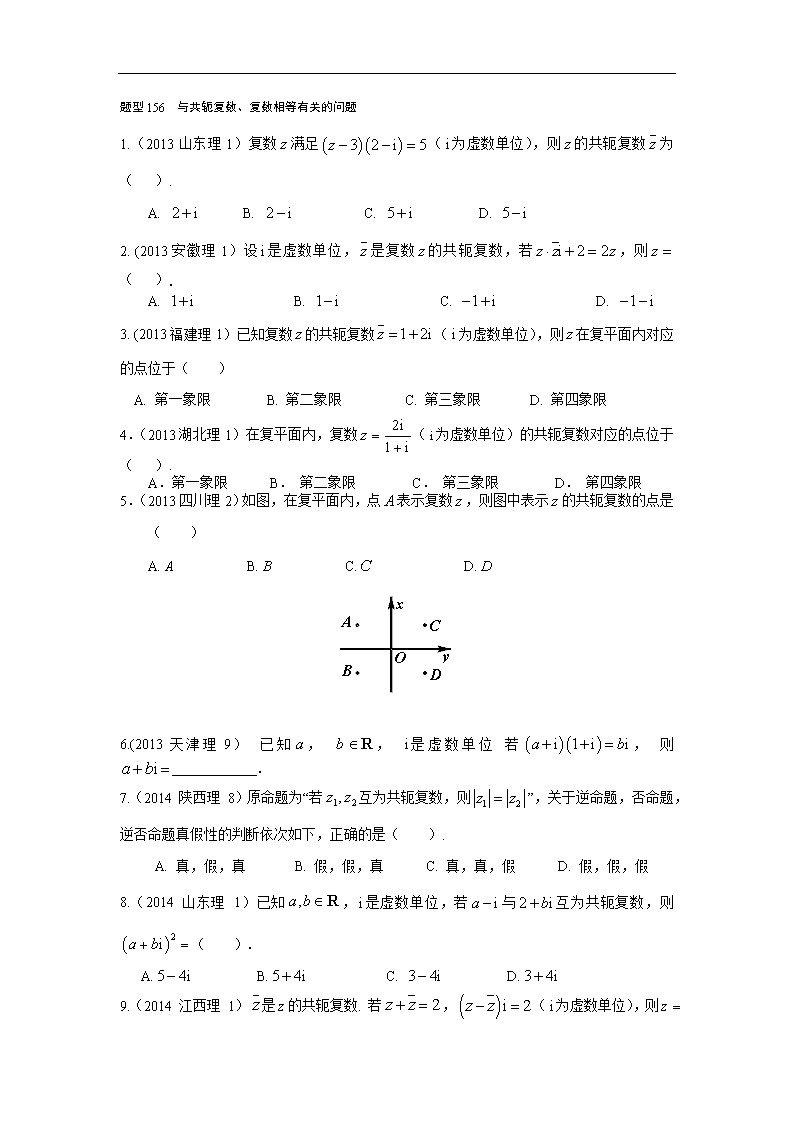

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018高考数学(理)复习-2013-2017高考分类汇编-第15章 数系的扩充与复数的引入
第十五章 数系的扩充与复数的引入 题型155 复数的概念及分类 1.(2015天津理9)是虚数单位,若复数 是纯虚数,则实数的值为 . 1. 解析 是纯虚数,所以,即. 2.(2016江苏2)复数,其中为虚数单位,则的实部是 . 2. 解析 由复数乘法法则可得,故的实部是. 3.(2016上海理2)设,其中为虚数单位,则 . 3.分析 在部分教材中,表示复数的虚部,表示复数的实部. 解析 因为,故.故填. 4.(2017天津理9)已知,为虚数单位,若为实数,则的值为 . 4.解析 为实数,则,解得. 5.(2017全国1卷理科3)设有下面四个命题: 若复数满足,则;若复数满足,则; 若复数满足,则;若复数,则. 其中的真命题为( ). A. B. C. D. 5. 解析 设,则,得到,所以.故正确; 若,满足,而,不满足,故不正确; 若,,则,满足,而它们实部不相等,不是共轭复数,故不正确; 实数没有虚部,所以它的共轭复数是它本身,也属于实数,故正确.故选B. 题型156 与共轭复数、复数相等有关的问题 1.(2013山东理1)复数满足(为虚数单位),则的共轭复数为( ). A. B. C. D. 2. (2013安徽理1)设是虚数单位,是复数的共轭复数,若,则( ). A. B. C. D. 3. (2013福建理1)已知复数的共轭复数(为虚数单位),则在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 4.(2013湖北理1)在复平面内,复数(为虚数单位)的共轭复数对应的点位于( ). A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限 5.(2013四川理2)如图,在复平面内,点表示复数,则图中表示的共轭复数的点是( ) A. B. C. D. 6.(2013天津理9) 已知, , 是虚数单位 若, 则 . 7.(2014 陕西理 8)原命题为“若互为共轭复数,则”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( ). A. 真,假,真 B. 假,假,真 C. 真,真,假 D. 假,假,假 8.(2014 山东理 1)已知,是虚数单位,若与互为共轭复数,则( ). A. B. C. D. 9.(2014 江西理 1)是的共轭复数. 若,(为虚数单位),则 ( ). A. B. C. D. 10.(2014 安徽理 1)设是虚数单位,表示复数的共轭复数.若,则( ). A. B. C. D. 11.(2014 大纲理 1)设,则z的共轭复数为( ). A. B. C. D. 12.(2014 福建理 1) 复数的共轭复数等于( ). A. B. C. D. 13.(2015广东理2)若复数(是虚数单位),则( ) A. B. C. D. 13. 解析 因为,所以.故选A. 14.(2015湖北理1)为虚数单位,的共轭复数为( ). A. B. C. D. 14. 解析 依题意可得:,故选A. 15.(2015全国二理2)若为实数,且,则( ). A. B. C. D. 15. 解析 由复数的运算律将左边直接展开可得.因为, 所以,解得.故选B. 16.(2015山东理2)若复数满足,其中为虚数单位,则( ) A. B. C. D. 16. 解析 因为,所以,所以.故选A. 17.(2016山东理1)若复数满足,其中为虚数单位,则( ). A. B. C. D. 17.B 解析 设,则 ,所以,即.故选B. 18.(2016天津理9)已知,是虚数单位,若,则的值为_______. 18.2 解析 ,则,所以,则. 19.(2107山东理2)已知,是虚数单位,若,,则( ). A.1或 B.或 C. D. 19. 解析 由,,得,所以.故选A. 20.(2017浙江11)已知,,(是虚数单位),则 , . 20.解析 由,,所以, 解得,所以,. 题型157 复数的模 1. (2013辽宁理1) 复数的的模为( ). A. B. C. D. 2.(2013江苏2)设(为虚数单位),则复数的模为 . 3. (2013陕西理6)设是复数,则下列命题中的假命题是( ). A. 若,则 B. 若,则 C. 若,则 D. 若,则 4. (2013重庆理11)已知复数(是虚数单位),则 . 5.(2015全国一理1)设复数满足,则( ) A. B. C. D. 5. 解析 由得,所以.故选A. 6.(2015陕西理11)设复数,若,则的概率为( ). A. B. C. D. 6. 解析 由可知, . 所以表示所示的阴影部分, 所以.故选D. 命题意图 考查复数的基本概念与知识,并与几何概型相结合,具备一定的新颖性. 7.(2015江苏3)设复数满足(是虚数单位),则的模为 . 7. 解析 解法一:设,则, 从而,即,故或, 从而. 解法二:由题意,故. 8.(2015重庆理11)设复数的模为,则________. 8. 解析 由题易得,故,. 9.(2016全国乙理2)设,其中,是实数,则( ). A. 1 B. C. D.2 9.B 解析 由,得,所以.故选B. 10.(2017江苏02)已知复数,其中是虚数单位,则 的模是 . 10.解析 解法一:,所以.故填. 解法二:.故填. 11.(2107全国3卷理科2)设复数满足,则( ). A. B. C. D.2 11.解析 由题意得,则.故选C. 题型158 复数的四则运算 1. (2013全国新课标卷理2)设复数满足,则( ). A. B. C. D. 2. (2013浙江理1)已知是虚数单位,则 A. B. C. D. 3.(2013广东理3)若复数满足,则在复平面内,对应的点的坐标是( ). A . B. C. D. 4.(2014 北京理 9)复数________. 5.(2014 江苏理 2)已知复数(为虚数单位),则的实部为 . 6.(2014 四川理 11)复数 . 7.(2014 天津理 1)是虚数单位,复数( ). A. B. C. D. 8.(2014 新课标1理2)( ). A. B. C. D. 9.(2014 辽宁理 2)设复数满足,则( ). A. B. C. D. 10.(2014 湖北理 1)为虚数单位,则( ). A. B. C. D. 11.(2014 湖南理 1)满足(是虚数单位)的复数( ). A. B. C. D. 12.(2014 广东理 2)已知复数满足则( ). A. B. C. D. 13.(2015北京理1)复数( ). A. B. C. D. 13. 解析 .故选A. 14.(2015福建理1)若集合(是虚数单位), ,则( ). A. B. C. D. 14. 解析 由已知得,故.故选C. 15.(2015湖南理1)已知(为虚数单位),则复数( ). A. B. C. D. 15. 解析 由题意得,.故选D. 16. (2015四川理2)设是虚数单位,则复数( ). A. B. C. D. 16. 解析 依题意可得:.故选C. 17.(2016全国丙卷2)若,则( ). A. B. C. D. 17.C 解析 因为所以.故选C. 18.(2016四川理2)设为虚数单位,则的展开式中含的项为( ). A. B. C. D. 18.A 解析 二项式展开的通项,则其展开式中含是当,即,则展开式中含的项为,故选A. 19.(2107全国2卷理科1)( ). A. B. C. D. 19.解析 .故选D. 题型159 复数的几何意义 1. (2013湖南理1)复数在复平面上对应的点位于( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限 2. (2013福建理1)已知复数的共轭复数(为虚数单位),则在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3.(2013湖北理1)在复平面内,复数(为虚数单位)的共轭复数对应的点位于( ). A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限 4.(2013四川理2)如图,在复平面内,点表示复数,则图中表示的共轭复数的点是( ) A. B. C. D. 5.(2014 新课标2理2)设复数,在复平面内的对应点关于虚轴对称, ,则( ). A. B. C. D. 6.(2014 重庆理 1)在复平面内表示复数的点位于( ). A.第一象限 B.第二象限 C.第三象限 D.第四象限 7.(2015安徽理1)设是虚数单位,则复数在复平面内所对应的点位于( ). A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 7. 解析 ,其对应的点坐标为,位于第二象限.故选B. 8.(2016北京理9)设,若复数在复平面内对应的点位于实轴上,则_______________. 8. 解析 由题意可得是实数,所以. 9.(2017北京理2)若复数在复平面内对应的点在第二象限,则实数的取值范围是( ). A. B. C. D. 9. 解析 由,则,即.故选B.查看更多