高考文科数学复习备课课件：第六节　对数与对数函数

高考文科数学复习备课课件：第六节　对数与对数函数

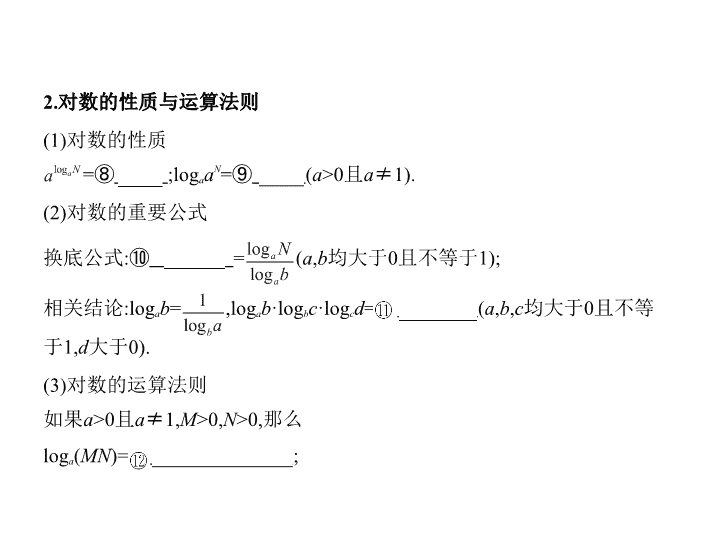
文数 课标 版 第六节　对数与对数函数 1.对数的概念 (1)对数的定义 一般地,如果①      a x = N ( a >0且 a ≠ 1)     ,那么数 x 叫做以 a 为底 N 的对数,记 作②      x =log a N      ,其中③      a      叫做对数的底数,④      N      叫做真数. (2)几种常见对数 教材研读 对数形式 特点 记法 一般对数 底数为 a ( a >0且 a ≠ 1) ⑤     log a N      常用对数 底数为10 ⑥     lg N      自然对数 底数为e ⑦     ln N      2.对数的性质与运算法则 (1)对数的性质   =⑧      N      ;log a a N =⑨      N      ( a >0且 a ≠ 1). (2)对数的重要公式 换底公式:⑩     log b N      =   ( a , b 均大于0且不等于1); 相关结论:log a b =   ,log a b ·log b c ·log c d =       log a d      ( a , b , c 均大于0且不等 于1, d 大于0). (3)对数的运算法则 如果 a >0且 a ≠ 1, M >0, N >0,那么 log a ( MN )=       log a M +log a N      ; log a   =       log a M -log a N      ; log a M n =        n log a M      ( n ∈R); lo   M n =   log a M ( m , n ∈R,且 m ≠ 0). 3.对数函数的图象与性质 a >1 0< a <1 图象     性质 定义域:(0,+ ∞ ) 值域:R 过点(1,0),即 x =1时, y =0 当 x >1时, y >0;当0< x <1时, y <0 当 x >1时, y <0;当0< x <1时, y >0 是(0,+ ∞ )上的增函数 是(0,+ ∞ )上的减函数 4.反函数 指数函数 y = a x ( a >0,且 a ≠ 1)与对数函数        y =log a x      ( a >0,且 a ≠ 1)互为 反函数,它们的图象关于直线        y = x      对称.   　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)若 MN >0,则log a ( MN )=log a M +log a N .   ( × ) (2)log a x ·log a y =log a ( x + y ).   ( × ) (3)函数 y =log 2 x 及 y =lo   (3 x )都是对数函数.   ( × ) (4)对数函数 y =log a x ( a >0,且 a ≠ 1)在(0,+ ∞ )上是增函数.( × ) (5)函数 y =ln   与 y =ln(1+ x )-ln(1- x )的定义域相同.   (√) 1.函数 y =   的定义域是   (　　) A.[1,2]　    B.[1,2)　    C.   　    D.   答案     D　由lo   (2 x -1) ≥ 0 ⇒ 0<2 x -1 ≤ 1 ⇒   < x ≤ 1. 2.如果lo   x y >1. 3.   +log 2   =   (　　) A.2　    B.2-2log 2 3 C.-2　    D.2log 2 3-2 答案     B       +log 2   =   -log 2 3=2-2log 2 3,选B. 4.   lg 25+lg 2-lg   -log 2 9·log 3 2的值是 　　　     . 答案 　-   解析 　原式=lg 5+lg 2+   -2=1+   -2=-   . 5.计算:log 2 3·log 3 4+(     = 　　　     . 答案　 4 解析     log 2 3·log 3 4+(     =   ·   +   =2+   =2+2=4. 考点一　对数式的化简与求值 典例1 　计算:(1)lg 25+lg 2·lg 50+(lg 2) 2 ; (2)   ; (3)(log 3 2+log 9 2)·(log 4 3+log 8 3). 解析 　(1)原式=(lg 2) 2 +(1+lg 5)lg 2+lg 5 2 =(lg 2+lg 5+1)lg 2+2lg 5 =(1+1)lg 2+2lg 5=2(lg 2+lg 5)=2. (2)原式=   =   =-   . 考点突破 (3)原式=log 3 2·log 4 3+log 3 2·log 8 3+log 9 2·log 4 3+log 9 2·log 8 3 =   ·   +   ·   +   ·   +   ·   =   +   +   +   =   =   . 方法技巧 解决对数的运算问题,主要的依据是对数的运算性质. 常用的方法有: (1)将真数化为底数的指数幂的形式进行化简; (2)将同底对数的和、差、倍合并; (3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底 公式的正用、逆用及变形应用; (4)利用常用对数中的lg 2+lg 5=1. 1-1 　设2 a =5 b = m ,且   +   =2,则 m = 　　　     . 答案        解析 　∵2 a =5 b = m >0,∴ a =log 2 m , b =log 5 m , ∴   +   =   +   =log m 2+log m 5=log m 10=2. ∴ m 2 =10,∴ m =   . 1-2 　已知log 18 9= a ,18 b =5,则log 36 45= 　　　     (用关于 a , b 的式子表示). 答案        解析 　解法一:因为18 b =5,所以log 18 5= b ,又log 18 9= a ,于是log 36 45=   =   =   =   . 解法二:因为log 18 9= a ,18 b =5,所以lg 9= a lg 18,lg 5= b lg 18,所以log 36 45=   =   =   =   =   . 考点二　对数函数的图象及应用 典例2 　(1)函数 f ( x )=lg   的大致图象为   (　　)   (2)当0< x ≤   时,4 x   ,解得 a >   ,∴   < a <1,故选B.   规律总结 利用对数函数的图象可求解的两类热点问题 (1)对一些可通过平移、对称变换作出其图象的对数型函数,在求解其 单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想求解. (2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用 数形结合法求解. 2-1     (2016河南焦作模拟)若函数 y = a | x | ( a >0,且 a ≠ 1)的值域为{ y | y ≥ 1},则 函数 y =log a | x |的图象大致是   (　　)   答案     B　若函数 y = a | x | ( a >0,且 a ≠ 1)的值域为{ y | y ≥ 1},则 a >1,故函数 y = log a | x |的图象大致是   故选B. 2-2　 设方程10 x =|lg(- x )|的两个根分别为 x 1 , x 2 ,则   (　　) A. x 1 x 2 <0　    B. x 1 x 2 =0 C. x 1 x 2 >1　    D.0< x 1 x 2 <1 答案     D　作出 y =10 x 与 y =|lg(- x )|的大致图象,如图.   显然 x 1 <0, x 2 <0. 不妨令 x 1 < x 2 ,则 x 1 <-1< x 2 <0, 所以1   =lg(- x 1 ),1   =-lg(- x 2 ), 此时1   <1   ,即lg(- x 1 )<-lg(- x 2 ), 由此得lg( x 1 x 2 )<0, 所以0< x 1 x 2 <1,故选D. 考点三　对数函数的性质及应用 典例3　 (1)设 a =log 3 2, b =log 5 2, c =log 2 3,则   (　　) A. a > c > b 　    B. b > c > a 　    C. c > b > a 　    D. c > a > b (2)函数 f ( x )=log a ( ax -3)在[1,3]上单调递增,则 a 的取值范围是   (　　) A.(1,+ ∞ )　    B.(0,1)　    C.   　    D.(3,+ ∞ ) 答案 　(1)D　(2)D 解析 　(1)∵   <2<3,1<2<   ,3>2, ∴log 3   log 2 2, ∴   < a <1,0< b <   , c >1,∴ c > a > b .故选D. (2)由于 a >0,且 a ≠ 1, ∴ u = ax -3为增函数, 因此 a >1. 又 u = ax -3在[1,3]上恒为正, ∴ a -3>0,即 a >3. 方法技巧 在解决与对数函数相关的比较大小或解不等式问题时,要优先考虑利用 对数函数的单调性来求解.在利用单调性时,一定要明确底数 a 的取值对 函数增减性的影响,及真数必须为正的限制条件. 3-1 　设 a , b , c 均为正数,且2 a =lo   a ,   =lo   b ,   =log 2 c ,则   (　　) A. a < b < c 　    B. c < b < a 　     C. c < a < b 　    D. b < a < c 答案     A　∵ a >0,∴2 a >1,∴lo   a >1, ∴0< a <   . ∵ b >0,∴0<   <1, ∴00,∴   >0, ∴log 2 c >0,∴ c >1. ∴0< a <   < b <1< c ,故选A. 3-2　 设函数 f ( x )=   若 f ( a )> f (- a ),则实数 a 的取值范围是   (　　) A.(-1,0) ∪ (0,1)　    B.(- ∞ ,-1) ∪ (1,+ ∞ ) C.(-1,0) ∪ (1,+ ∞ )　    D.(- ∞ ,-1) ∪ (0,1) 答案     C　解法一:①若 a >0,则- a <0, ∴log 2 a >lo   a ⇒ log 2 a >log 2   ⇒ a >   ⇒ a >1. ②若 a <0,则- a >0, ∴lo   (- a )>log 2 (- a ) ⇒ log 2   >log 2 (- a ) ⇒ -   >- a ⇒ a >-1.∴-1< a <0. 由①②可知 a ∈(-1,0) ∪ (1,+ ∞ ). 解法二:特殊值验证. 令 a =2, f (2)=log 2 2=1, f (-2)=lo   [-(-2)]=-1, 满足 f ( a )> f (- a ),故排除A、D. 令 a =-2, f (-2)=lo   [-(-2)]=-1, f (-(-2))= f (2)=1, 不满足 f ( a )> f (- a ),故排除B.