- 2021-06-11 发布 |
- 37.5 KB |
- 9页
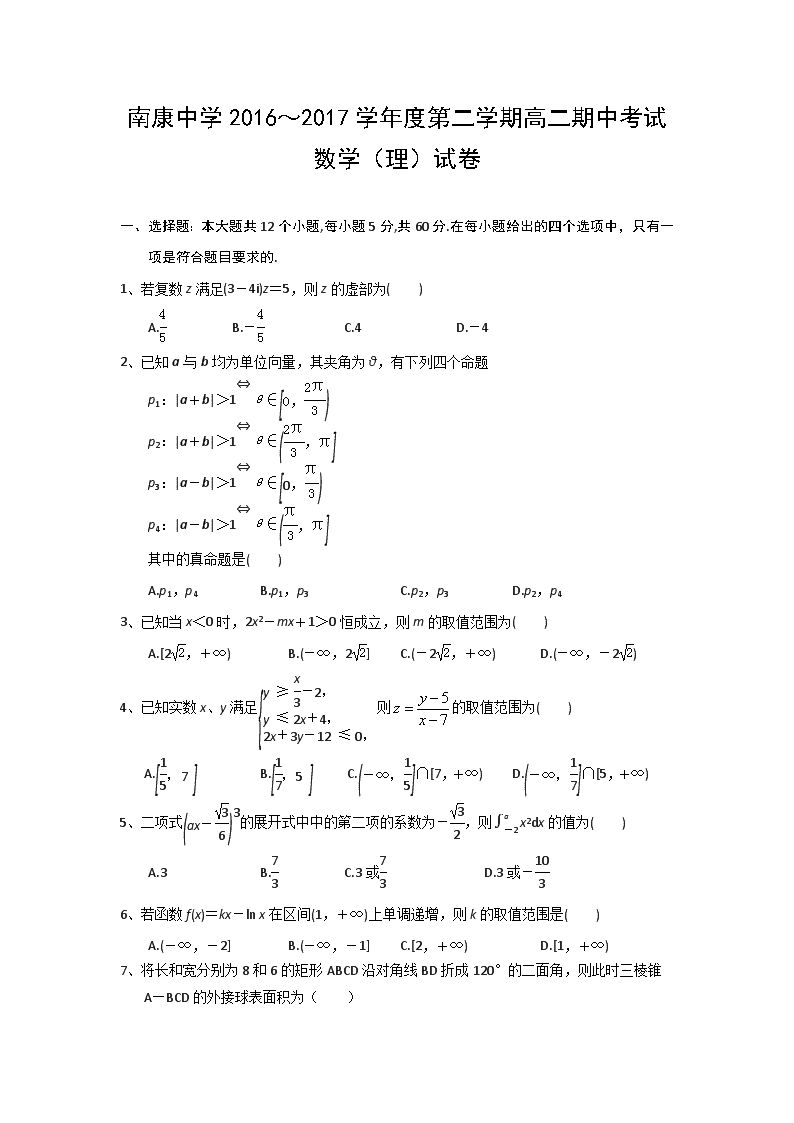

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届江西省南康中学高二下学期期中考试(2017-04)
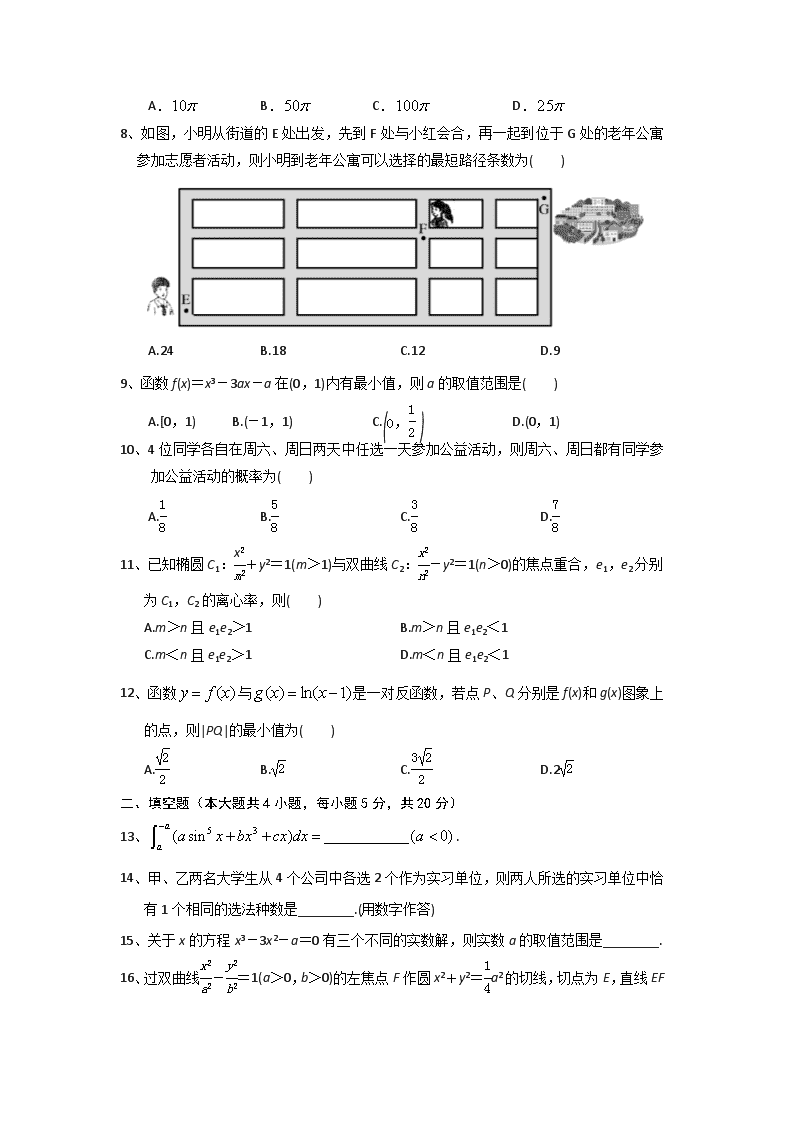
南康中学2016~2017学年度第二学期高二期中考试 数学(理)试卷 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1、若复数z满足(3-4i)z=5,则z的虚部为( ) A. B.- C.4 D.-4 2、已知a与b均为单位向量,其夹角为θ,有下列四个命题 p1:|a+b|>1⇔θ∈ p2:|a+b|>1⇔θ∈ p3:|a-b|>1⇔θ∈ p4:|a-b|>1⇔θ∈ 其中的真命题是( ) A.p1,p4 B.p1,p3 C.p2,p3 D.p2,p4 3、已知当x<0时,2x2-mx+1>0恒成立,则m的取值范围为( ) A.[2,+∞) B.(-∞,2] C.(-2,+∞) D.(-∞,-2) 4、已知实数x、y满足则的取值范围为( ) A. B. C.∩[7,+∞) D.∩[5,+∞) 5、二项式的展开式中中的第二项的系数为-,则x2dx的值为( ) A.3 B. C.3或 D.3或- 6、若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是( ) A.(-∞,-2] B.(-∞,-1] C.[2,+∞) D.[1,+∞) 7、将长和宽分别为8和6的矩形ABCD沿对角线BD折成120°的二面角,则此时三棱锥A—BCD的外接球表面积为( ) A. B. C. D. 8、如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( ) A.24 B.18 C.12 D.9 9、函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是( ) A.[0,1) B.(-1,1) C. D.(0,1) 10、4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( ) A. B. C. D. 11、已知椭圆C1:+y2=1(m>1)与双曲线C2:-y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则( ) A.m>n且e1e2>1 B.m>n且e1e2<1 C.m<n且e1e2>1 D.m<n且e1e2<1 12、函数与是一对反函数,若点P、Q分别是f(x)和g(x)图象上的点,则|PQ|的最小值为( ) A. B. C. D.2 二、填空题(本大题共4小题,每小题5分,共20分) 13、 . 14、甲、乙两名大学生从4个公司中各选2个作为实习单位,则两人所选的实习单位中恰有1个相同的选法种数是________.(用数字作答) 15、关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________. 16、过双曲线-=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为E,直线EF交双曲线右支于点P,若=(+),则双曲线的离心率是________. 三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.) 17、(本小题满分10分)三男三女站成一排, ⑴男生彼此相邻,女生也彼此相邻的站法有多少种? ⑵男生彼此不相邻,女生也彼此不相邻的站法有多少种? 18、(本小题满分12分)已知函已知函数f(x)=4sin3xcos x-2sin xcos x-cos 4x. (1)求函数f(x)的最小正周期及单调递增区间;[来源] (2)求f(x)在区间上的最大值和最小值. 19、(本小题满分12分)如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2, ∠ABC=∠DBC=120°,E,F分别为AC,DC的中点. (1)求证:EF⊥BC; (2)求二面角E-BF-C的正弦值. 20、(本小题满分12分)已知函数f(x)=x2ex. (1)求f(x)的单调区间; (2)证明: 21、(本小题满分12分)已知椭圆E:+=1(a>b>0)的半焦距为c,原点O到经过两点 (c,0),(0,b)的直线的距离为c. (1)求椭圆E的离心率; (2)如图,AB是圆M:(x+2)2+(y-1)2=的一条直径, 若椭圆E经过A,B两点,求椭圆E的方程. 22、(本小题满分12分)已知函数f(x)=ax++c(a>0)的图象在点(1,f(1))处的切线方程 为y=x-1. (1)用a表示出b,c; (2)若f(x)≥ln x在[1,+∞)上恒成立,求a的取值范围; (3)证明:1+++…+>ln(n+1)+(n≥1). 南康中学2016~2017学年度第二学期高二期中考试 数学(理)参考答案 命题人:卓邦南 审题人:李雪峰 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1—5:AACBC 6—10:DCBDD 11—12:AD 二、填空题(本大题共4小题,每小题5分,共20分) 13、 14、24 15、 (-4,0) 16、 三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.) 17、解:⑴捆绑法:种…………………………5分 ⑵插空法:先排男生种,有4个空;女生只能插前3个空或后3个空,有种 种……………………………………10分 18、解 f(x)=2sin xcos x-cos 4x =-sin 2xcos 2x-cos 4x=-sin 4x-cos 4x =-sin.…………………………………………3分 (1)函数f(x)的最小正周期T==. 令2kπ+≤4x+≤2kπ+,k∈Z, 得+≤x≤+,k∈Z. 所以f(x)的单调递增区间为,k∈Z.……6分 (2)因为0≤x≤,所以≤4x+≤. 此时-≤sin≤1, 所以-≤-sin≤,即-≤f(x)≤. 所以f(x)在区间上的最大值和最小值分别为,-.…………12分 19、法一 (1)证明 由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂 直BC的直线为z轴,建立如图所示空间直角坐标系.易得B(0,0,0), A(0,-1,),D(,-1,0),C(0,2,0). 因而E(0,,),F, 所以=,=(0,2,0), 因此·=0.从而⊥,所以EF⊥BC.………………6分 (2)解 平面BFC的一个法向量为n1=(0,0,1). 设平面BEF的法向量n2=(x,y,z), 又=,=. 由得其中一个n2=(1,-,1). 设二面角E-BF-C大小为θ,且由题意知θ为锐角,则 cos〈n1,n2〉==,∴cos θ=, 因此sin θ==,即所求二面角的正弦值为.………………12分 20、(1)解 f′(x)=x(x+2)ex. 令f′(x)=x(x+2)ex=0,则x1=-2,x2=0. 当x变化时,f′(x),f(x)的变化情况如下表 x (-∞,-2) -2 (-2,0) 0 (0,+∞) f′(x) + 0 - 0 + f(x) ↗ 极大值 ↘ 极小值 ↗ 所以函数f(x)的单调递减区间为(-2,0),单调递增区间为(-∞,-2),(0, +∞).………………………………………………………………………………6分 (2)证明 由(1)知f(x)的单调递增区间为(-∞,-2),单调递减区间为(-2,0), 所以当x∈(-∞,0]时,f(x)最大值=f(-2)=. 因为当x∈(-∞,-2]时,f(x)>0,f(0)=0, 所以当x∈(-∞,0]时,f(x)最小值=f(0)=0. 所以f(x)最大值-f(x)最小值=. 所以对∀x1,x2∈(-∞,0],都有f(x1)-f(x2)≤f(x)最大值-f(x)最小值=.…………12分 21、解 (1)过点(c,0),(0,b)的直线方程为bx+cy-bc=0, 则原点O到该直线的距离d==, 由d=c,得a=2b=2,解得离心率=.……………………5分 (2)法一 由(1)知,椭圆E的方程为x2+4y2=4b2.① 依题意,圆心M(-2,1)是线段AB的中点,且|AB|=. 易知,AB与x轴不垂直,设其方程为y=k(x+2)+1,代入①得(1+4k2)x2+8k(2k+1) x+4(2k+1)2-4b2=0, 设A(x1,y1),B(x2,y2),则x1+x2=-, x1x2=, 由x1+x2=-4,得-=-4,解得k=, 从而x1x2=8-2b2. 于是|AB|=|x1-x2| ==, 由|AB|=,得=,解得b2=3, 故椭圆E的方程为+=1.…………………………………………12分 法二 由(1)知,椭圆E的方程为x2+4y2=4b2,② 依题意,点A,B关于圆心M(-2,1)对称,且|AB|=,设A(x1,y1),B(x2,y2),则x+4y=4b2,x+4y=4b2,两式相减并结合x1+x2=-4,y1+y2=2, 得-4(x1-x2)+8(y1-y2)=0, 易知AB与x轴不垂直,则x1≠x2,所以AB的斜率kAB==, 因此直线AB的方程为y=(x+2)+1, 代入②得x2+4x+8-2b2=0, 所以x1+x2=-4,x1x2=8-2b2, 于是|AB|= |x1-x2| ==. 由|AB|=,得=,解得b2=3, 故椭圆E的方程为+=1. 22、(1)解 f′(x)=a-,则有解得………………3分 (2)解 由(1)知,f(x)=ax++1-2a. 令g(x)=f(x)-ln x=ax++1-2a-ln x,x∈[1,+∞), 则g(1)=0,g′(x)=a--==, (ⅰ)当0<a<时,>1. 若1<x<,则g′(x)<0,g(x)是减函数,所以g(x)<g(1)=0,即f(x)<ln x. 故f(x)≥ln x在[1,+∞)上不成立. (ⅱ)当a≥时,≤1. 若x>1,则g′(x)>0,g(x)是增函数,所以g(x)>g(1)=0, 即f(x)>ln x,故当x≥1时,f(x)≥ln x. 综上所述,所求a的取值范围为.……………………7分 (3)证明 法一 由(2)知:当a≥时,有f(x)≥ln x(x≥1). 令a=,有f(x)=≥ln x(x≥1), 且当x>1时,>ln x. 令x=,有ln <=, 即ln(k+1)-ln k<,k=1,2,3,…,n. 将上述n个不等式依次相加得ln(n+1)<++, 整理得1+++…+>ln(n+1)+.…………………………12分 法二 用数学归纳法证明. ①当n=1时,左边=1,右边=ln 2+<1,不等式成立. ②假设n=k时,不等式成立,即 1+++…+>ln(k+1)+. 那么1+++…++>ln(k+1)++=ln(k+1)+. 由(2)知:当a≥时,有f(x)≥ln x(x≥1). 令a=,有f(x)=≥ln x(x≥1). 令x=,得:≥ln =ln(k+2)-ln(k+1). ∴ln(k+1)+≥ln(k+2)+. ∴1+++…++>ln(k+2)+. 这就是说,当n=k+1时,不等式也成立.查看更多