- 2021-06-11 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年江苏省包场高级中学高二5月月考数学(理)试题(Word版)
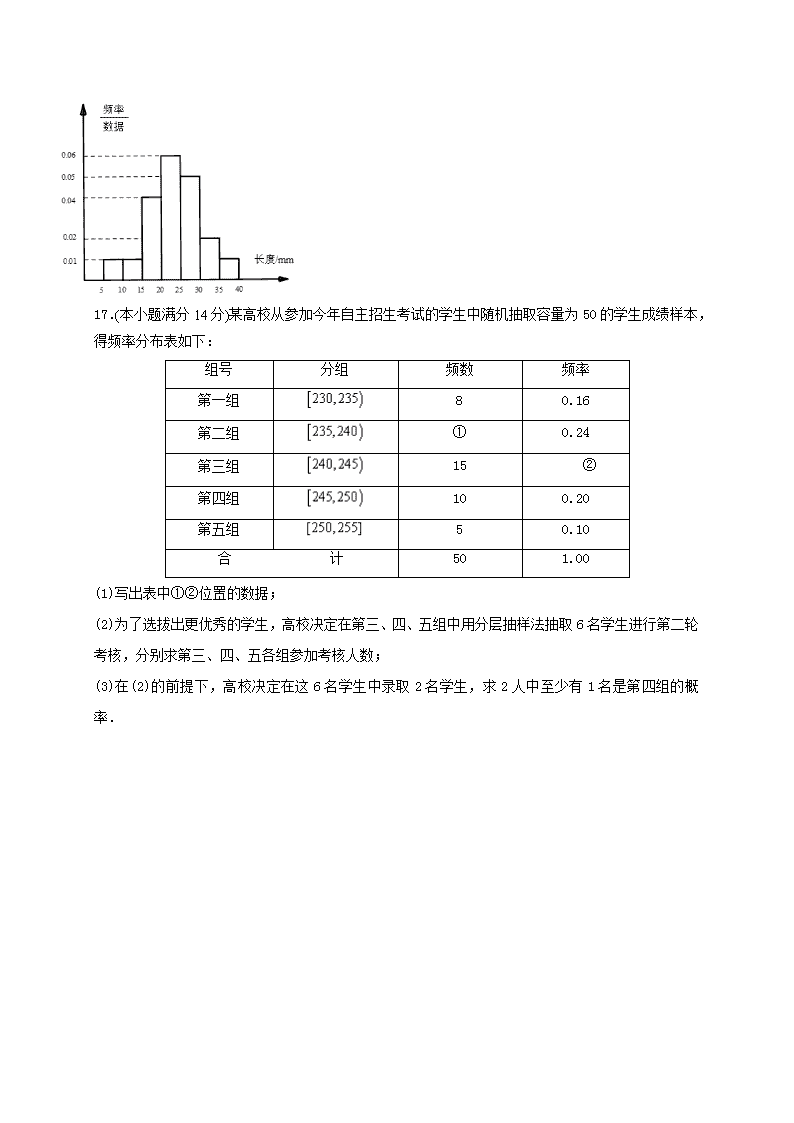
2017-2018学年江苏省包场高级中学高二5月月考数学理 2018.5.24 一、填空题 1.设(为虚数单位),则复数的模为 2. 根据如图所示的伪代码,可知输出的结果为 . 3. 某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件. 4.已知=++,则x= 5. 已知的展开式中第五项的系数与第三项的系数的比是10:1,则展开式中含的项为 6. 射击运动员甲、乙两人在6次射击中取得的成绩分别为: 第1次 第2次 第3次 第4次 第5次 第6次 甲 8环 9环 x环 10环 6环 7环 乙 7环 9环 7环 8环 y环 9环 若甲、乙两人的平均成绩都是8环,则方差较小的运动员是 7.若展开式中系数为21,则____________ 8. 现在某类病毒记作,其中正整数,(,)可以任意选取,则都取到奇数的概率为 9. 从集合中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 . 10.由数字0、、、、、组成没有重复数字的五位数,其中小于的偶数共有 个 11.在共有2 013项的等差数列{an}中,有等式(a1+a3+…+a2 013)-(a2+a4+…+a2 012)=a1007成立;类比上述性质,在共有2 011项的等比数列{bn}中,相应的有等式 _______ 成立 12.某种产品有4只次品和6只正品,每只产品均不相同且可区分,今每次取出一只测试,直到4只次品全测出为止,则最后一只次品恰好在第五次测试时,被发现的不同情况种数是__ ___ 13.已知(其中,且),若 ,则 = 14. 设是从-1,0,1这三个整数中取值的数列, 若,则中数字0的个数为 . 二 解答题 15.(本小题满分14分)如图,在直四棱柱中,底面为平行四边形,. 求证:(1)∥平面; (2)平面⊥平面. 16. (本小题满分14分)某棉纺厂为了解一批棉花的质量,从中随机抽取了若干根棉花纤维并测得长度数据(单位:mm),所得数据都在区间[5,40]中,其频率分布直方图如图所示,其中数据在区间[5,10)的频数为5.(1)共抽取了多少根棉花纤维? (2)抽取的样本中有多少根棉花纤维的长度小于20mm? (3)该批棉花中纤维长度不小于15mm的棉花约占多少?并说明理由. 17.(本小题满分14分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下: 组号 分组 频数 频率 第一组 8 0.16 第二组 ① 0.24 第三组 15 ② 第四组 10 0.20 第五组 5 0.10 合 计 50 1.00 (1)写出表中①②位置的数据; (2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数; (3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率. 18. (本小题满分16分)设命题:函数的定义域为R;命题:函数在上单调递减. (1)若命题“”为真,“”为假,求实数的取值范围; (2)若关于的不等式的解集为M;命题为真命题时, 的取值集合为N.当是的充分不必要条件时,求实数的取值范围. 19. (本小题满分10分)已知展开式的二项式系数和为512, 且(1)求的值; (2)求的值;(3)求被6整除的余数. 20. (本小题满分10分)某社区举办北京奥运知识宣传活动,现场的“抽卡有奖游戏”特别引人注目,游戏规则是:盒子中装有8张形状大小相同的精美卡片,卡片上分别印有“奥运福娃”或“奥运会徽”,要求参加游戏的4人从盒子中轮流抽取卡片,一次抽2张,抽取后不放回,直到4人中一人一次抽到2张“奥运福娃” 卡才能得到奖并终止游戏. (1)游戏开始之前,一位高中生问:盒子中有几张“奥运会徽” 卡?主持人说:若从盒中任抽2张卡片不都是“奥运会徽” 卡的概率为.请你回答有几张“奥运会徽” 卡呢? (2)现有甲、乙、丙、丁4人参加游戏,约定甲、乙、丙、丁依次抽取.用表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求的概率分布及的数学期望. 21(本小题满分10分)把正整数按从小到大顺序排列成下列数表,数表中第行共有个正整数: 设是位于数表中从上往下数第行、从左往右数第个数 (1)若,求的值; (2)记,求数列的通项公式; (3)猜想与的大小关系,并证明你的结论. 22. (本小题满分10分) 用四个不同字母组成一个含个字母的字符串,要求由开始,相邻两个字母不同. 例如时,排出的字符串是;时排出的字符串是,……, 如图所示.记这含个字母的所有字符串中,排在最后一个的字母仍是的字符串的种数为. (1)试用数学归纳法证明:; (2)现从四个字母组成的含个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是的概率为,求证: 23. (本小题满分16分)如图,已知椭圆C:+=1(a>b>0)的右焦点为F(1,0). (1)已知椭圆C的下顶点为A,直线AF与椭圆C交于点B,且=3,求椭圆C的方程; F A B x y O (2)已知D(2,0),椭圆C上存在点P,满足=,求椭圆C的离心率的取值范围. 24.(本小题满分16分)设函数,在和处有两个极值点,其中 (1)求实数的取值范围; (2)若(为自然对数的底数),求的最大值. 答案:1、 2、7 3、 18 4、3 5、 6、乙 7、1或-2 8、 9. 10.300 11、 12、576 13、 14、11 16.(1)数据落在[5,10)的频率为0.01×5=0.05,又因为频数是5, 所以抽取了100根的棉花纤维长度; ……………………………………………4分 (2) 因为(0.01+0.01+0.04)×5×100=30, 所以抽取的样本中有30根棉花纤维的长度小于20mm; …………………………………8分 (3) 因为1-(0.01+0.01)×5=0.9, 所以抽取的样本中有90%的纤维长度不小于15 mm, ………………………12分 所以该批棉花中纤维长度不小于15 mm的棉花约占90%. ……………………………14分 17 18. 19. 20. 21. 22. 23. 由=3得(1,b)=3(x-1,y),则 解得x=,y=, …………………………4分 代入椭圆得a2=2,b2=1, 故椭圆C的方程为+y2=1. …………………………6分 (2)设P(x0,y0),于是+=1. ① …………………………8分 因为=,即PD2=2PF2,所以(x0-2)2+y=2(x0-1)2+2y,即x+y=2. ② …………………………10分 联立①②,并注意到a2=b2+1,解得x=2a2-a2b2=a2(3-a2). …………………………12分 因为-a≤x0≤a,所以0≤x≤a2. 于是0≤a2(3-a2)≤a2,即2≤a2≤3,亦即≤a≤. …………………………14分 所以≤≤,即≤≤. 故椭圆C的离心率的取值范围是. …………………………16分 24. 【解析】(Ⅰ) , 则由题意则方程有两个正根, 故, 解得.故实数的取值范围是, …………6分 (Ⅱ), 又, =,…………10分 设,故,构造函数,…………12分 ,所以在上是减函数,…………14分 ,的最大值为…………16分查看更多