2013届高考数学一轮复习 二元一次不等式(组)与简单的线性规划问题
2013届高考一轮复习 二元一次不等式(组)与简单的线性规划问题
一、选择题
1、若则点(m,n)必在( )
A.直线x+y=1的左下方
B.直线x+y=1的右上方
C.直线x+2y=1的左下方
D.直线x+2y=1的右上方
2、满足条件 的可行域中整点的个数为( )
A.3 B.4
C.5 D.6
3、设不等式组 所表示的平面区域是,平面区域与关于直线3x-4y-9=0对称.对于中的任意一点A与中的任意一点B,|AB|的最小值等于( )
A. B.4
C. D.2
4、设变量x,y满足约束条件 则z=2x+y的最大值为( )
A.-2 B.4
C.6 D.8
5、在平面直角坐标系中,若不等式组 (a为常数)所表示的平面区域的面积等于2,则a的值为( )
A.-5 B.1
C.2 D.3
6、某班计划用少于100元的钱购买单价分别为2元和1元的大小彩色气球装点联欢晚会的会场,根据需要,大球数不少于10个,小球数不少于20个,请你给出几种不同的购买方案?
7、已知(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
A.a<1或a>24 B.a=7或a=24
C.-7
-1,
∵
∴1=2,解得a=3.
6、解:设可购买大球x个,小球y个.
依题意有
其整数解为 …
都符合题目要求(满足2x+y-100<0即可).
7、 C
8、B
解析:将直线y=x+1与y=2x-1联立解得A(2,3),据题意即为最优解,
又点A必在直线x+y=m上,代入求得m=5.
9、B
解析:设需使用甲型货车x辆,乙型货车y辆,运输费用z元,
根据题意,得线性约束条件
求线性目标函数z=400x+300y的最小值.
解得当 时 200.
二、填空题
10、
解析:作出可行域如图:
由图可知直线y=-x与y=-x+3平行,若最大值只有一个,则直线y=a必须在直线y=2x与y=-x+3的交点(1,2)的下方,故.
11、 -9
解析:如图,作出可行域为阴影部分,
由 得
即A(3,6),经过分析可知直线z=x-2y经过A点时目标函数z=x-2y取最小值为-9.
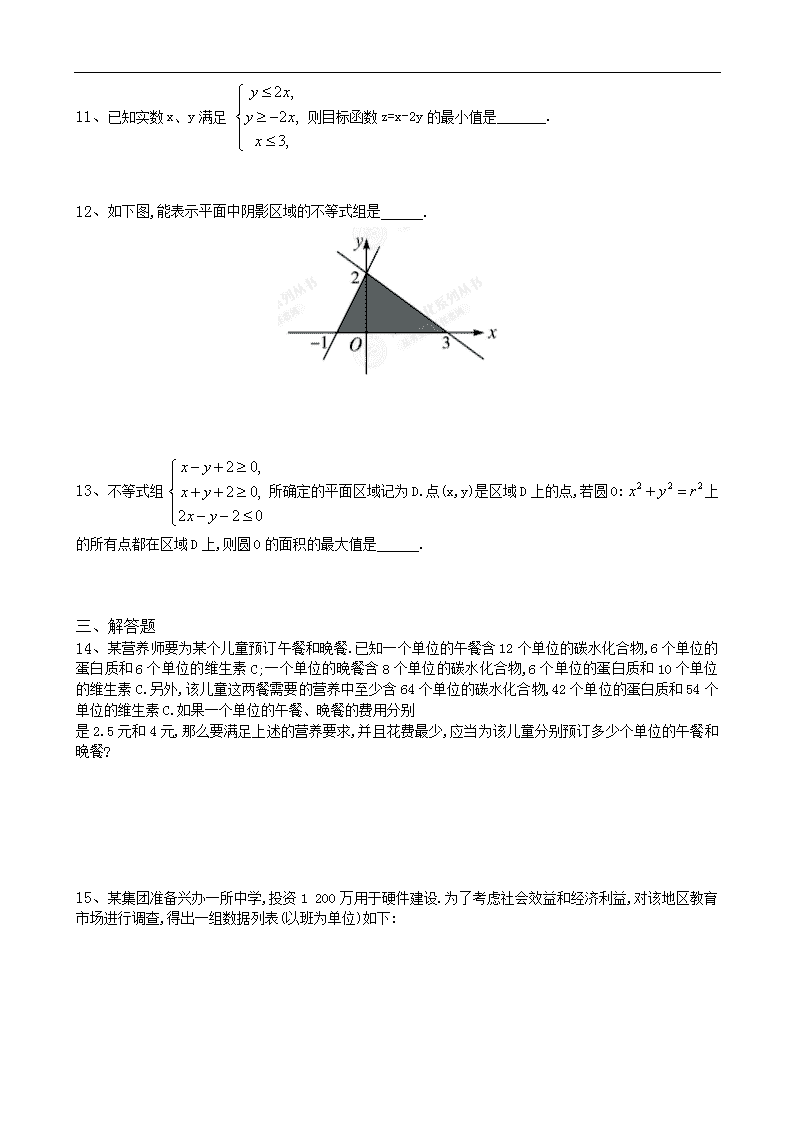
12、
13、
解析:画出不等式组 所表示的平面区域(略),其中直线离原点最近的距离为故r的最大值为所以圆O的面积的最大值是.
三、解答题
14、 解:方法一:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,
则依题意得z=2.5x+4y,且x,y满足 即
z在可行域的四个顶点A(9,0),B(4,3),C(2,6),D(0,8)处的值分别是
.=22.5,
.
.
..
比较之最小,因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
方法二:设需要预订满足要求的午餐和晚餐分别为x个单位和y个单位,所花的费用为z元,
则依题意得z=2.5x+4y,且x,y满足 即
让目标函数表示的直线2.5x+4y=z在可行域上平移,
由此可知z=2.5x+4y在B(4,3)处取得最小值.
因此,应该为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.
15、 解:设初中x个班,高中y个班,
则
设年利润为s,则
...2x-2..6y=1.2x+2y.
作出①、②表示的平面区域,如图,易知当直线1.2x+2y=s过点A时,s有最大值.
由 解得A(18,12).
∴..6(万元).
即学校可规划初中18个班,高中12个班,可获最大年利润为45.6万元.
16、解:作出二元一次不等式组 表示的平面区域,如图所示.
由u=3x-y,得y=3x-u,表示斜率为3,在y轴上的截距为-u,随u变化的一组平行线,
由图可知,当直线y=3x-u经过可行域上的C点时,截距-u最大,即u最小,
解方程组 得C(-2,3),
∴.
当直线y=3x-u经过可行域上的B点时,截距-u最小,即u最大,
解方程组 得B(2,1),
∴.
∴u=3x-y的最大值是5,最小值是-9.