2018-2019学年湖北省钢城四中高二上学期期中考试数学（文）试题 Word版

2018-2019学年湖北省钢城四中高二上学期期中考试数学（文）试题 Word版

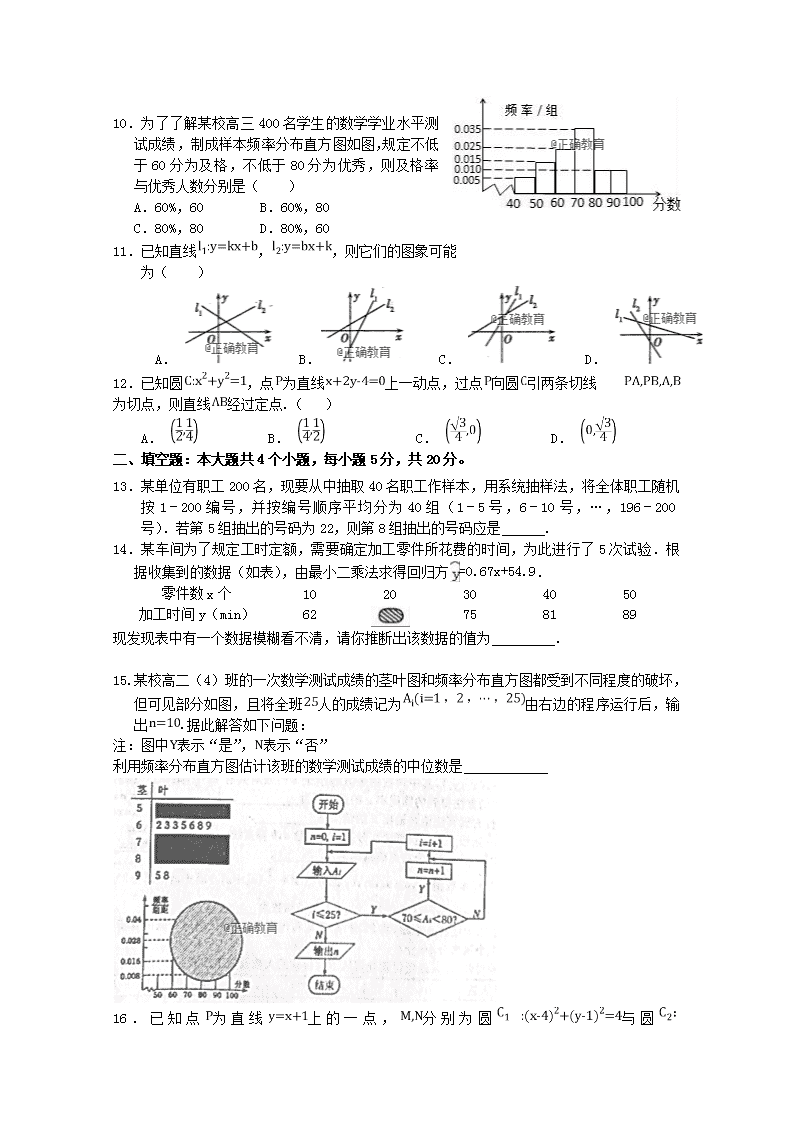
钢城四中2018—2019学年（上）期中考试卷 学科 数学（文科）‎ 年级 高二 命题 曾鹏环 审核 胡世忠 时间 ‎120‎ 分值 ‎150’‎ 一、选择题（本大题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，‎ 只有一项是符合题目要求的）。‎ ‎1．已知与之间的一组数据：‎ 则与的线性回归方程为必过点（ ）‎ A． B． C． D． ‎ ‎2．如图所示的茎叶图记录了甲、乙两组各五名学生在一次英语听力 测试中的成绩（单位：分），已知甲组数据的中位数为15，乙组 数据的平均数为16.8，则x，y的值分别为（ ）‎ A． 2，5 B． 5，5 C． 5，8 D． 8，8‎ ‎3． 若直线与互相垂直，则等于（ ）‎ A． -3 B． 1 C． 0或 D． 1或－3‎ ‎4．某工厂生产A、B、C三种不同型号的产品，其数量之比依次是3：4：7，现在用分层抽样的方法抽出样本容量为n的样本，样本中A型号产品有15件，那么n等于（　　）‎ A．50 B．60 C．70 D．80‎ ‎5．将八进制数化为十进制的数是_______；再化为三进制的数_______‎ A.454, 121211 B.464，12121 C.454，12121 D.464，121211‎ ‎6．某小组有3名男生和2名女生，从中任选2名学生参加演讲比赛，那么互斥而不对立的两个事件是（ ）‎ A．至少有1名男生和至少有1名女生 B．至多有1名男生和都是女生 C．至少有1名男生和都是女生 D．恰有1名男生和恰有2名男生 ‎7. 若圆：与圆：外切，则=‎ A. 21 B.19 C.9 D.-11‎ ‎8．某学校从编号依次为001，002，…，900的900个学生中用系统抽样（等间距抽样）的方法抽取一个样本，已知样本中相邻的两个编号分别为053，098，则样本中最大的编号为（ ）‎ A． 853 B． 854 C． 863 D． 864‎ ‎9. 执行如图所示的程序框图，则输出的数值是（ ）‎ A． B． C． D． ‎ ‎10．为了了解某校高三400名学生的数学学业水平测试成绩，制成样本频率分布直方图如图，规定不低于60分为及格，不低于80分为优秀，则及格率与优秀人数分别是（　　）‎ A．60%，60 B．60%，80 ‎ C．80%，80 D．80%，60‎ ‎11．已知直线，，则它们的图象可能 为（　　）‎ A． B． C． D． ‎ ‎12．已知圆，点为直线上一动点，过点向圆引两条切线为切点，则直线经过定点.（ ）‎ A． B． C． D． ‎ 二、填空题：本大题共4个小题，每小题5分，共20分。‎ ‎13．某单位有职工200名，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1﹣200编号，并按编号顺序平均分为40组（1﹣5号，6﹣10号，…，196﹣200号）．若第5组抽出的号码为22，则第8组抽出的号码应是　 　．‎ ‎14．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据（如表），由最小二乘法求得回归方=0.67x+54.9．‎ 零件数x个 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 加工时间y（min）‎ ‎62‎ ‎75‎ ‎81‎ ‎89‎ 现发现表中有一个数据模糊看不清，请你推断出该数据的值为　 　．‎ ‎15.某校高二（4）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，且将全班人的成绩记为由右边的程序运行后，输出.据此解答如下问题：‎ 注：图中表示“是”，表示“否”‎ 利用频率分布直方图估计该班的数学测试成绩的中位数是　 　‎ ‎16．已知点为直线上的一点，分别为圆 与圆 ‎ 上的点,则的最大值为___________.‎ 三、解答题 ‎17．已知菱形的一边AD的所在直线方程为，一条对角线的两个端点分别为和.‎ ‎(1) 求对角线所在直线的方程;(2) 求菱形的边BC所在直线的方程.‎ ‎18．孝感星河天街购物广场某营销部门随机抽查了100名市民在2017年国庆长假期间购物广场的消费金额，所得数据如表，已知消费金额不超过3千元与超过3千元的人数比恰为3:2．‎ ‎（1）试确定， ， ， 的值，并补全频率分布直方图（如图）；‎ ‎（2）用分层抽样的方法从消费金额在、和的三个群体中抽取7人进行问卷调查，则各小组应抽取几人？若从这7人中随机选取2人，则此2人来自同一群体的概率是多少？‎ ‎19.求与圆外切且直线相切于点的圆的方程。‎ ‎20．设x2+2ax+b2=0是关于x的一元二次方程．‎ ‎（1）若a是从0，1，2，3四个数个中任取的一个数，b是从0，1，2三个数中任取的一个数，求方程有实根的概率；‎ ‎（2）若a是从区间[0，3]上任取一个数，b是从区间[0，2]上任取一个数，求方程有实根的概率．‎ ‎21．武汉车天地关于某品牌汽车的使用年限（年）和所支出的维修费用（千元）由如表的统计资料：‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2.1‎ ‎3.4‎ ‎5.9‎ ‎6.6‎ ‎7.0‎ ‎（1）画出散点图并判断使用年限与所支出的维修费用是否线性相关；如果线性相关，求回归直线方程；‎ ‎（2）若使用超过8年，维修费用超过1.5万元时，车主将处理掉该车，估计第10年年底时，车主是否会处理掉该车？‎ ‎（）‎ ‎22．某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．‎ ‎（1）求n的值；‎ ‎（2）把在前排就坐的高二代表队6人分别记为a，b， ‎ c，d，e，f，现随机从中抽取2人上台抽奖．求 a和b至少有一人上台抽奖的概率．‎ ‎（3）抽奖活动的规则是：代表通过操作按键使电脑自 ‎ 动产生两个[0，1]之间的均匀随机数x，y，并按 如图所示的程序框图执行．若电脑显示“中奖”，‎ 则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．‎ ‎2018-2019学年度上学期期中考试文科数学答案 ‎1D 2 3D 4C 5A 6D 7 C 8C 9B 10C 11C 12B ‎13 37 14 68 15 73.516 6‎ ‎17．已知菱形的一边所在直线方程为，一条对角线的两个端点分别为和.‎ ‎(1) 求对角线和所在直线的方程;‎ ‎(2) 求菱形另三边所在直线的方程 ‎(1)因为和所以设AC的方程为 ，则 ，解得 ‎ 所以直线AC方程为，即 设AC中点坐标为 ，因为ABCD为菱形，所以直线BD与直线AC垂直，且平分线段AC AC垂直平分线的斜率 所以BD的直线方程为 ，即 5分 ‎(2) 因为在直线上，不妨设是AB的方程 则DC直线与AB直线平行且过点C，所以DC的直线方程为 AB与BD的交点B坐标为，解得 ‎ 所以BC直线方程为 10分 ‎18．武汉星河天街购物广场某营销部门随机抽查了100名市民在2017年国庆长假期间购物广场的消费金额，所得数据如表，已知消费金额不超过3千元与超过3千元的人数比恰为3:2．‎ ‎（1）试确定， ， ， 的值，并补全频率分布直方图（如图）；‎ ‎（2）用分层抽样的方法从消费金额在、和的三个群体中抽取7人进行问卷调查，则各小组应抽取几人？若从这7人中随机选取2人，则此2人来自同一群体的概率是多少？‎ ‎（1）根据题意，有 解得 ∴， ．　‎ 补全频率分布直方图如图所示：‎ ‎6分 ‎（2）根据题意，消费金额在内的人数为（人），记为， ，‎ 消费金额在内的人数为（人），记为1,2,3．　‎ 消费金额在内的人数为（人），记为， ．‎ 则从这7人中随机选取2人的所有的基本事件为： ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ，共21种，‎ 设“2人来自同一群体”为事件，则事件包含的基本事件有， ， ， ， ，共5种，由古典概型概率公式得．‎ 所以此2人来自同一群体的概率是。 12分 ‎19.求与圆外切且直线相切于点的圆的方程。‎ ‎ 12‎ ‎20．设x2+2ax+b2=0是关于x的一元二次方程．‎ ‎（1）若a是从0，1，2，3四个数个中任取的一个数，b是从0，1，2三个数中任取的一个数，求方程有实根的概率；‎ ‎（2）若a是从区间[0，3]上任取一个数，b是从区间[0，2]上任取一个数，求方程有实根的概率．‎ 解：方程有实根的充要条件为：△=（2a）2﹣4b2≥0，即a2≥b2．‎ ‎（1）基本事件共有12个，其中（0，0），（1，0），（1，1），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）满足条件，则． 6分 ‎（2 ）试验的全部结果构成的区域为{（a，b）|0≤a≤3，0≤b≤2}，‎ 满足题意的区域为：{（a，b）|0≤a≤3，0≤b≤2，a≥b}，‎ 所以，所求概率为．… 12分 ‎21．武汉车天地关于某品牌汽车的使用年限（年）和所支出的维修费用（千元）由如表的统计资料：‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2.1‎ ‎3.4‎ ‎5.9‎ ‎6.6‎ ‎7.0‎ ‎（1）画出散点图并判断使用年限与所支出的维修费用是否线性相关；如果线性相关，求回归直线方程；‎ ‎（2）若使用超过8年，维修费用超过1.5万元时，车主将处理掉该车，估计第10年年底时，车主是否会处理掉该车？‎ ‎（）‎ ‎（1）作出散点图如图：‎ ‎ ‎ 由散点图可知使用年限与所支出的维修费是线性相关的．　 4分 列表如下：‎ 由以上数据可得，‎ 所以，‎ 故回归直线方程为. ‎ ‎ 8分 ‎（2）当时， ，‎ 因此可估计使用10年维修费用是12.8千元，‎ 即维修费用是1.28万元，‎ 因为维修费用低于1.5万元，所以车主不会处理该车． 12分 ‎22．某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．‎ ‎（1）求n的值；‎ ‎（2）把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖．求a和b至少有一人上台抽奖的概率．‎ ‎（3）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．‎ 解：（1）由题意可得，∴n=160； 4分 ‎（2）高二代表队6人，从中抽取2人上台抽奖的基本事件有（a，b），（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b．f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共15种，其中a和b至少有一人上台抽奖的基本事件有9种，‎ ‎∴a和b至少有一人上台抽奖的概率为=； 4分 ‎（3）由已知0≤x≤1，0≤y≤1，点（x，y）在如图所示的正方形OABC内，‎ 由条件得到的区域为图中的阴影部分 由2x﹣y﹣1=0，令y=0可得x=，令y=1可得x=1‎ ‎∴在x，y∈[0，1]时满足2x﹣y﹣1≤0的区域的面积为=‎ ‎∴该代表中奖的概率为=． 4分