高中数学必修5：1_2应用举例（同步练习）

高中数学必修5：1_2应用举例（同步练习）

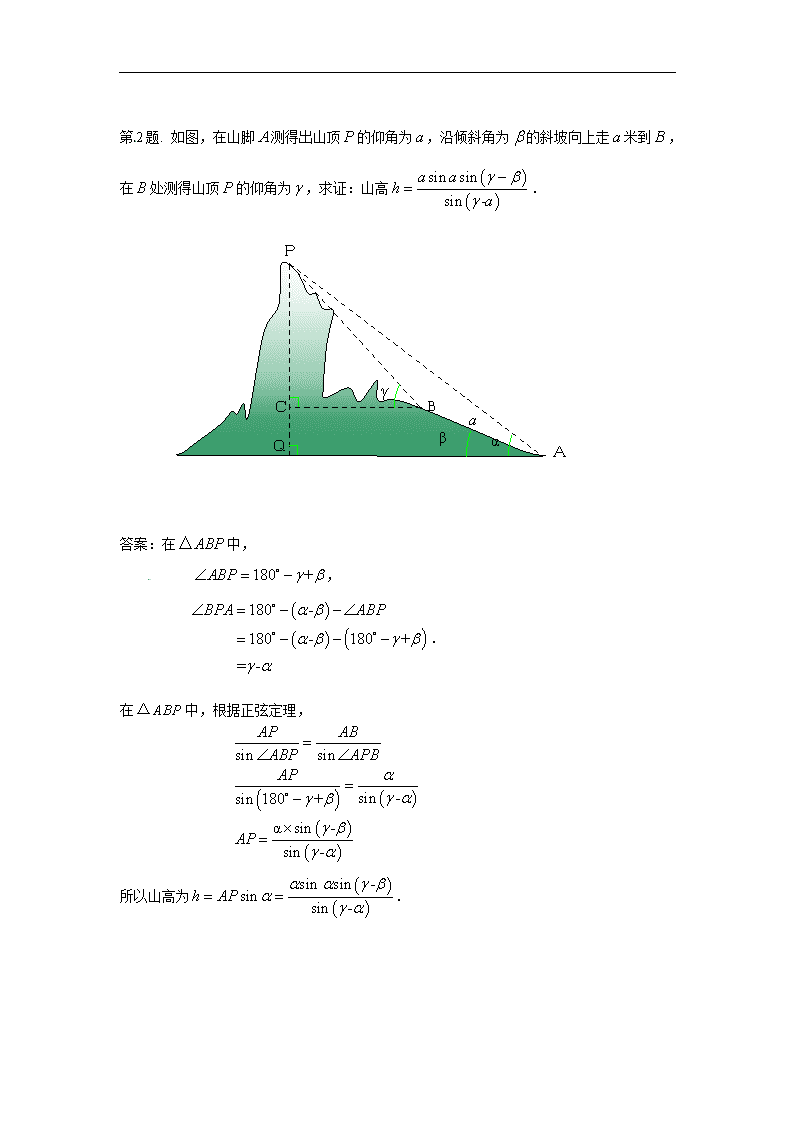
第1题. 如图，一艘船以32.2n mile/h的速度向正北航行．在Ａ处看灯塔Ｓ在船的北偏东的方向，30 min后航行到Ｂ处，在Ｂ处看灯塔在船的北偏东的方向，已知距离此灯塔6.5n mile以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？‎ A 南 北 西 东 ‎65‎ B S 答案：在中，mile，，‎ 根据正弦定理，，‎ ‎，‎ 到直线的距离是 ‎（cm）．‎ 所以这艘船可以继续沿正北方向航行．‎ 第2题. 如图，在山脚测得出山顶的仰角为，沿倾斜角为的斜坡向上走米到，在处测得山顶的仰角为，求证：山高．‎ Ａ Ｑ B Ｃ Ｐ 答案：在中，‎ ‎　　　　　，‎ ‎　　　　　．‎ 在中，根据正弦定理，‎ ‎　　　　　　　　‎ 所以山高为．‎ 第3题. 测山上石油钻井的井架的高，从山脚测得m，塔顶的仰角是．‎ 已知山坡的倾斜角是，求井架的高．‎ Ａ D Ｂ Ｃ 答案：在中，m，‎ ‎，‎ ‎，‎ 根据正弦定理，‎ 井架的高约为‎9.3m．‎ C B A ‎(6739)第4题. 如图，货轮在海上以35n mile / h的速度沿着方位角（从指北方向顺时针转到目标方向线的水平角）为的方向航行．为了确定船位，在B点观察灯塔A的方位角是，航行半小时后到达Ｃ点，观察灯塔A的方位角是．求货轮到达Ｃ点时与灯塔 A的距离（精确到１ n mile）．‎ 答案：在中，＝n mile ，，‎ ‎，，‎ 根据正弦定理，，‎ ‎（nmile）． ‎ 货轮到达Ｃ点时与灯塔的距离是约4.29n mile．‎ 第5题. 轮船A和轮船B在中午12时离开海港C，两艘轮船的航行方向之间的夹角为，轮船A的航行速度是25 n mile/h，轮船B的航行速度是15 n mile/h，下午2时两船之间的距离是多少？‎ 答案：70 n mile．‎ 第6题. 如图，已知一艘船从30 n mile/h的速度往北偏东的A岛行驶，计划到达A岛后停留10 min后继续驶往B岛，B岛在A岛的北偏西的方向上．船到达Ｃ处时是上午10时整，此时测得B岛在北偏西的方向，经过20 min到达Ｄ处，测得B岛在北偏西的方向，如果一切正常的话，此船何时能到达B岛？‎ ‎30‎ ‎60‎ B C A ‎20 min 答案：在中，‎ ‎　　　　　‎ ‎，‎ ‎（n mile），‎ 根据正弦定理，‎ ‎，，‎ ‎．‎ 在中，‎ ‎，，‎ ‎．‎ 根据正弦定理，‎ ‎　　　　，‎ 就是 ‎，‎ ‎（n mile）．‎ ‎(n mile)．‎ 如果这一切正常，此船从Ｃ开始到Ｂ所需要的时间为：‎ ‎（min）‎ 即约１小时26分59秒．所以此船约在11时27分到达Ｂ岛．‎ 第7题. 一架飞机在海拔‎8000m的高度飞行，在空中测出前下方海岛两侧海岸俯角分别是，计算这个海岛的宽度． ‎ ‎8000m ‎27‎ P Q ‎ ‎ 答案：约‎5821.71m．‎ 第8题. 一架飞机从A地飞到B到，两地相距700km．飞行员为了避开某一区域的雷雨云层，从机场起飞后，就沿与原来的飞行方向成角的方向飞行，飞行到中途，再沿与原来的飞行方向成夹角的方向继续飞行直到终点．这样飞机的飞行路程比原来路程‎700km远了多少？‎ A ‎700km ‎21‎ B C 答案：在中，km，，‎ 根据正弦定理，，‎ ‎，‎ ‎，‎ ‎（km），‎ 所以路程比原来远了约km． ‎ 第9题. 为测量某塔的高度，在A，B两点进行测量的数据如图所示，求塔的高度．‎ 答案：在，，（m）．‎ 根据正弦定理，，． ‎ 塔的高度为（m）．‎ A ‎76.5‎ B 第10题. A，B两地相距‎2558m，从A，B两处发出的 两束探照灯光照射在上方一架飞机的机身上（如图），飞机离 两个探照灯的距离是多少？飞机的高度是多少？‎ 答案：飞机离A处控照灯的距离是‎4801.53m，‎ 飞机离B处探照灯的距离是‎4704.21m，‎ 飞机的高度是约‎4574.23m．‎ 第11题. 一架飞以‎326km/h的速度，沿北偏东的航向从城市A出发向城市B飞行，18min以后，飞机由于天气原因按命令改飞另一个城市C，问收到命令时飞机应该沿什么航向飞行，此时离城市C的距离是多少？‎ 答案：=km，‎ 在中，根据余弦定理：‎ 根据正弦定理： ，‎ ‎，‎ ‎，．‎ 在中，根据余弦定理：‎ ‎，‎ ‎，‎ ‎．‎ 在中，根据余弦定理：‎ ‎ ‎ ‎，‎ ‎．‎ ‎， ‎ ‎，‎ ‎．‎ 所以，飞机应该以南偏西的方向飞行，飞行距离约km．‎ C D B A E ‎ ‎ 第12题. 飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔20250m，速度为‎1000km/h，飞行员先看到山顶的俯角为，经过150s后又看到山顶的俯角为，求山顶的海拔高度（精确到‎1m）．‎ ‎ ‎ 答案：飞行在150秒内飞行的距离是m，‎ 根据正弦定理，，这里是飞机看到山顶的俯角为时飞机与山顶的距离．飞机与山顶的海拔的差是：‎ ‎(m)，‎ 山顶的海拔是m．‎ 第13题. 一个人在建筑物的正西点，测得建筑物顶的仰角是，这个人再从点向南走到点，再测得建筑物顶的仰角是，设，间的距离是．‎ 证明：建筑物的高是．‎ 答案：设建筑物的同度是，建筑物的底部是，‎ 则．‎ 是直角三角形，是斜边，‎ 所以，‎ ‎，‎ ‎．‎ 所以，．‎ ‎ ‎