2020届二轮复习直线平面垂直的判定与性质课件（32张）（全国通用）

2020届二轮复习直线平面垂直的判定与性质课件（32张）（全国通用）

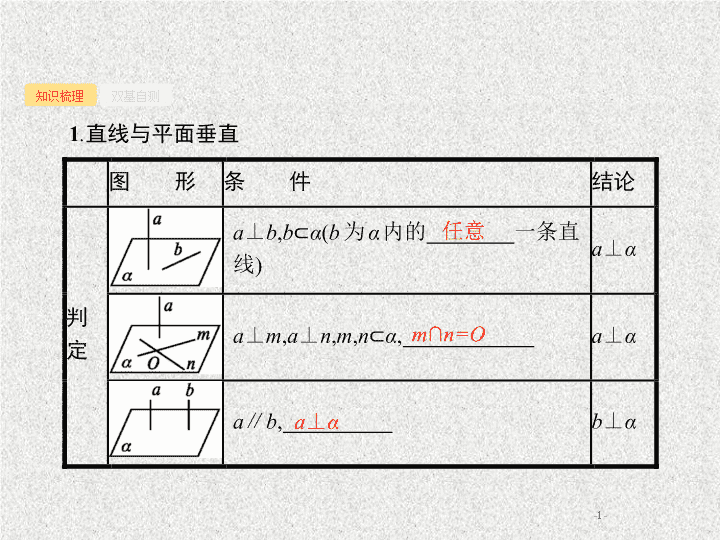
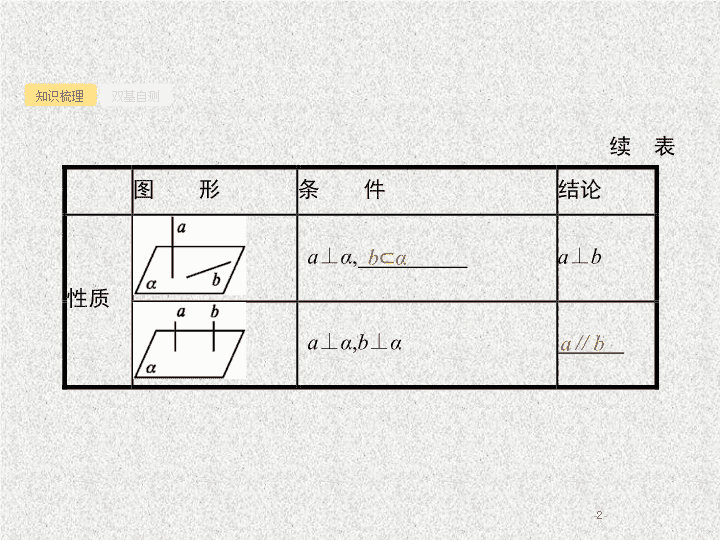
- 1 - 知识梳理 双基自测 1 . 直线与平面 垂直 任意 m ∩ n=O a ⊥ α 　 - 2 - 知识梳理 双基自测 b ⊂ α a ∥ b - 3 - 知识梳理 双基自测 2 . 平面与平面垂直 (1) 平面与平面垂直的定义 两个平面相交 , 如果它们所成的二面角是 　　　　　　　　 , 就说这两个平面互相垂直 .   直 二面角 - 4 - 知识梳理 双基自测 (2) 判定定理与性质 定理 垂线 交线 　 l ⊥ α - 5 - 知识梳理 双基自测 3 . 常用结论 (1) 线面平行或垂直的有关结论 ① 若两平行线中的一条垂直于一个平面 , 则另一条也垂直于这个平面 . ② 若一条直线垂直于一个平面 , 则它垂直于这个平面内的任何一条直线 ( 证明线线垂直的一个重要方法 ) . ③ 垂直于同一条直线的两个平面平行 . ④ 一条直线垂直于两平行平面中的一个 , 则这一条直线与另一个平面也垂直 . ⑤ 两个相交平面同时垂直于第三个平面 , 它们的交线也垂直于第三个平面 . (2) 证明线面垂直时 , 易忽视平面内两条线为相交线这一条件 . 2 - 6 - 知识梳理 双基自测 3 4 1 5 1 . 下列结论正确的打 “ √ ” , 错误的打 “ ×” . (1) 已知直线 a , b , c , 若 a ⊥ b , b ⊥ c , 则 a ∥ c. ( 　　 ) (2 ) 若直线 l 与平面 α 内的无数条直线都垂直 , 则 l ⊥ α . ( 　　 ) (3) 设 m , n 是两条不同的直线 , α 是一个平面 , 若 m ∥ n , m ⊥ α , 则 n ⊥ α . ( 　　 ) (4) 若两平面垂直 , 则其中一个平面内的任意一条直线垂直于另一个平面 . ( 　　 ) (5) 若平面 α 内的一条直线垂直于平面 β 内的无数条直线 , 则 α ⊥ β . ( 　　 ) × × √ × × - 7 - 知识梳理 双基自测 2 3 4 1 5 2 . 设 α , β 为两个不同的平面 , 直线 l ⊂ α , 则 “ l ⊥ β ” 是 “ α ⊥ β ” 成立的 ( 　　 ) A . 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 A 解析 依题意 , 由 l ⊥ β , l ⊂ α 可以推出 α ⊥ β ; 反过来 , 由 α ⊥ β , l ⊂ α 不能推出 l ⊥ β . 因此 “ l ⊥ β ” 是 “ α ⊥ β ” 成立的充分不必要条件 , 故选 A . - 8 - 知识梳理 双基自测 2 3 4 1 5 3 . 将图 1 中的等腰直角三角形 ABC 沿斜边 BC 的中线折起得到空间四面体 A-BCD ( 如图 2), 则在空间四面体 A-BCD 中 , AD 与 BC 的位置关系是 ( 　　 ) A. 相交且垂直 B. 相交但不垂直 C. 异面且垂直 D. 异面但不垂直 C 解析 在题图 1 中的等腰直角三角形 ABC 中 , 斜边上的中线 AD 就是斜边上的高 , 则 AD ⊥ BC , 翻折后如题图 2, AD 与 BC 变成异面直线 , 而原线段 BC 变成两条线段 BD , CD , 这两条线段与 AD 垂直 , 即 AD ⊥ BD , AD ⊥ CD , 故 AD ⊥ 平面 BCD , 所以 AD ⊥ BC. - 9 - 知识梳理 双基自测 2 3 4 1 5 4 .P 为 △ ABC 所在平面外一点 , O 为 P 在平面 ABC 内的射影 . (1) 若 P 到 △ ABC 三边距离相等 , 且 O 在 △ ABC 的内部 , 则 O 是 △ ABC 的 　　　　　 心 ;   (2) 若 PA ⊥ BC , PB ⊥ AC , 则 O 是 △ ABC 的 　　　　　 心 ;   (3) 若 PA , PB , PC 与底面所成的角相等 , 则 O 是 △ ABC 的 　　　　 心 . 内 垂 外 解析 (1) P 到 △ ABC 三边距离相等 , 且 O 在 △ ABC 的内部 , 可知 O 到 △ ABC 三边距离相等 , 即 O 是 △ ABC 的内心 ;(2) 由 PO ⊥ 平面 ABC 且 BC ⊂ 平面 ABC , 得 PO ⊥ BC , 又 PA ⊥ BC , PO 与 PA 是平面 POA 内两条相交直线 , 所以 BC ⊥ 平面 POA , 从而 BC ⊥ AO. 同理 AC ⊥ BO , 所以 O 是 △ ABC 的垂心 ;(3) 由 PA , PB , PC 与底面所成的角相等 , 易得 Rt △ POA ≌ Rt △ POB ≌ Rt △ POC , 从而 OA=OB=OC , 所以 O 是 △ ABC 的外心 . - 10 - 知识梳理 双基自测 2 3 4 1 5 5 . 如图 , PA ⊥☉ O 所在平面 , AB 是 ☉ O 的直径 , C 是 ☉ O 上一点 , AE ⊥ PC , AF ⊥ PB , 给出下列结论 : ① AE ⊥ BC ; ② EF ⊥ PB ; ③ AF ⊥ BC ; ④ AE ⊥ 平面 PBC , 其中真命题的序号是 　　　　　　　　 .   ①② ④ 解析 ① 因为 AE ⊂ 平面 PAC , BC ⊥ AC , BC ⊥ PA , 所以 AE ⊥ BC , 故 ① 正确 ; ② 因为 AE ⊥ PC , AE ⊥ BC , PB ⊂ 平面 PBC , 所以 AE ⊥ PB , 又 AF ⊥ PB , EF ⊂ 平面 AEF , 所以 EF ⊥ PB , 故 ② 正确 ; ③ 因为 AF ⊥ PB , 若 AF ⊥ BC , 则 AF ⊥ 平面 PBC , 则 AF ∥ AE , 与已知矛盾 , 故 ③ 错误 ; 由 ① 可知 ④ 正确 . - 11 - 考点 1 考点 2 考点 3 例 1 如图所示 , 在四棱锥 P-ABCD 中 , AB ⊥ 平面 PAD , AB ∥ CD , PD=AD , E 是 PB 的中点 , F 是 DC 上的点 , 且 DF= AB , PH 为 △ PAD 中 AD 边上的高 . 求证 :(1) PH ⊥ 平面 ABCD ; (2) EF ⊥ 平面 PAB. 思考 证明线面垂直的常用方法有哪些 ? - 12 - 考点 1 考点 2 考点 3 证明 (1) 因为 AB ⊥ 平面 PAD , PH ⊂ 平面 PAD , 所以 PH ⊥ AB. 因为 PH 为 △ PAD 中 AD 边上的高 , 所以 PH ⊥ AD. 因为 AB ∩ AD=A , AB ⊂ 平面 ABCD , AD ⊂ 平面 ABCD , 所以 PH ⊥ 平面 ABCD. (2) 如图 , 取 PA 的中点 M , 连接 MD , ME. 因为 E 是 PB 的中点 , 所以四边形 MEFD 是平行四边形 , 所以 EF ∥ MD. 因为 PD=AD , 所以 MD ⊥ PA . 因为 AB ⊥ 平面 PAD , 所以 MD ⊥ AB. 因为 PA ∩ AB=A , 所以 MD ⊥ 平面 PAB , 所以 EF ⊥ 平面 PAB. - 13 - 考点 1 考点 2 考点 3 解题心得 1 . 证明线面垂直的方法 : 一是线面垂直的判定定理 ; 二是利用面面垂直的性质定理 ; 三是平行线法 ( 若两条平行线中的一条垂直于这个平面 , 则另一条也垂直于这个平面 ) . 2 . 解题时 , 注意线线、线面与面面关系的相互转化 ; 另外 , 在证明线线垂直时 , 要注意题中隐含的垂直关系 , 如等腰三角形底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形 ( 或给出线段长度 , 经计算满足勾股定理 ) 、直角梯形等 . - 14 - 考点 1 考点 2 考点 3 (1) 求证 : AP ⊥ 平面 ABCE ; (2) 记平面 PAB 与平面 PCE 相交于直线 l , 求证 : AB ∥ l. - 15 - 考点 1 考点 2 考点 3 同理 , AP ⊥ AC. ∵ AC ∩ AE=A , AC ⊂ 平面 ABCE , AE ⊂ 平面 ABCE , ∴ AP ⊥ 平面 ABCE. (2) ∵ AB ∥ CE , 且 CE ⊂ 平面 PCE , AB ⊄ 平面 PCE , ∴ AB ∥ 平面 PCE. 又平面 PAB ∩ 平面 PCE=l , ∴ AB ∥ l. - 16 - 考点 1 考点 2 考点 3 例 2 如图 , 四边形 ABCD 为菱形 , G 为 AC 与 BD 的交点 , BE ⊥ 平面 ABCD . ( 1) 证明 : 平面 AEC ⊥ 平面 BED ; (2) 若 ∠ ABC= 120 ° , AE ⊥ EC , 三棱锥 E-ACD 的体积 为 , 求该三棱锥的侧面积 . 思考 证明面面垂直的常用方法有哪些 ? - 17 - 考点 1 考点 2 考点 3 (1) 证明 因为四边形 ABCD 为菱形 , 所以 AC ⊥ BD. 因为 BE ⊥ 平面 ABCD , 所以 AC ⊥ BE. 故 AC ⊥ 平面 BED. 又因为 AC ⊂ 平面 AEC , 所以平面 AEC ⊥ 平面 BED . - 18 - 考点 1 考点 2 考点 3 - 19 - 考点 1 考点 2 考点 3 解题心得 1 . 两个平面互相垂直是两个平面相交的特殊情形 . 2 . 由平面和平面垂直的判定定理可知 , 要证明平面与平面垂直 , 可转化为从现有直线中寻找平面的垂线 , 即证明线面垂直 . 3 . 平面和平面垂直的判定定理的两个条件 : l ⊂ α , l ⊥ β , 缺一不可 . - 20 - 考点 1 考点 2 考点 3 对点训练 2 在四棱柱 ABCD-A 1 B 1 C 1 D 1 中 , 四边形 ABCD 为平行四边形 , AA 1 ⊥ 平面 ABCD , ∠ BAD= 60 ° , AB= 2, BC= 1, AA 1 = , E 为 A 1 B 1 的中点 . (1) 求证 : 平面 A 1 BD ⊥ 平面 A 1 AD ; (2) 求多面体 A 1 E-ABCD 的体积 . - 21 - 考点 1 考点 2 考点 3 (1) 证明 ∵ AB= 2, AD=BC= 1, ∠ BAD= 60 ° , ∴ BD 2 +AD 2 =AB 2 , ∴ BD ⊥ AD , ∵ AA 1 ⊥ 平面 ABCD , BD ⊂ 平面 ABCD , ∴ BD ⊥ AA 1 , 又 AA 1 ∩ AD=A , AA 1 ⊂ 平面 A 1 AD , AD ⊂ 平面 A 1 AD , ∴ BD ⊥ 平面 A 1 AD , 又 BD ⊂ 平面 A 1 BD , ∴ 平面 A 1 BD ⊥ 平面 A 1 AD. - 22 - 考点 1 考点 2 考点 3 - 23 - 考点 1 考点 2 考点 3 考向一 　 平行与垂直关系的证明 例 3 如图 , 在直三棱柱 ABC-A 1 B 1 C 1 中 , D , E 分别为 AB , BC 的中点 , 点 F 在侧棱 B 1 B 上 , 且 B 1 D ⊥ A 1 F , A 1 C 1 ⊥ A 1 B 1 . 求证 :(1) 直线 DE ∥ 平面 A 1 C 1 F ; (2) 平面 B 1 DE ⊥ 平面 A 1 C 1 F. 思考 处理平行与垂直关系的综合问题的主要数学思想方法是什么 ? - 24 - 考点 1 考点 2 考点 3 证明 (1) 在直三棱柱 ABC-A 1 B 1 C 1 中 , A 1 C 1 ∥ AC. 在 △ ABC 中 , 因为 D , E 分别为 AB , BC 的中点 , 所以 DE ∥ AC , 于是 DE ∥ A 1 C 1 . 又因为 DE ⊄ 平面 A 1 C 1 F , A 1 C 1 ⊂ 平面 A 1 C 1 F , 所以直线 DE ∥ 平面 A 1 C 1 F. (2) 在直三棱柱 ABC-A 1 B 1 C 1 中 , A 1 A ⊥ 平面 A 1 B 1 C 1 . 因为 A 1 C 1 ⊂ 平面 A 1 B 1 C 1 , 所以 A 1 A ⊥ A 1 C 1 . 又因为 A 1 C 1 ⊥ A 1 B 1 , A 1 A ⊂ 平面 ABB 1 A 1 , A 1 B 1 ⊂ 平面 ABB 1 A 1 , A 1 A ∩ A 1 B 1 =A 1 , 所以 A 1 C 1 ⊥ 平面 ABB 1 A 1 . 因为 B 1 D ⊂ 平面 ABB 1 A 1 , 所以 A 1 C 1 ⊥ B 1 D. 又因为 B 1 D ⊥ A 1 F , A 1 C 1 ⊂ 平面 A 1 C 1 F , A 1 F ⊂ 平面 A 1 C 1 F , A 1 C 1 ∩ A 1 F=A 1 , 所以 B 1 D ⊥ 平面 A 1 C 1 F. 因为直线 B 1 D ⊂ 平面 B 1 DE , 所以 平面 B 1 DE ⊥ 平面 A 1 C 1 F. - 25 - 考点 1 考点 2 考点 3 考向二 　 探索性问题中的平行与垂直关系 例 4 如图 , 在四棱锥 P-ABCD 中 , 底面 ABCD 是菱形 , ∠ DAB= 45 ° , PD ⊥ 平面 ABCD , PD=AD= 1, 点 E 为 AB 上一点 , 且 点 F 为 PD 中点 . (1) 若 k = , 求证 : 直线 AF ∥ 平面 PEC ; (2) 是否存在一个常数 k , 使得平面 PED ⊥ 平面 PAB ? 若存在 , 求出 k 的值 ; 若不存在 , 请说明理由 . 思考 探索性问题的一般处理方法是什么 ? - 26 - 考点 1 考点 2 考点 3 (1) 证明 如图 , 作 FM ∥ CD 交 PC 于点 M. ∵ 点 F 为 PD 中点 , ∴ FM= CD. ∵ k= , ∴ AE= AB=FM. 又 ∵ FM ∥ CD ∥ AB , ∴ 四边形 AEMF 为平行四边形 . ∴ AF ∥ EM. ∵ AF ⊄ 平面 PEC , EM ⊂ 平面 PEC , ∴ 直线 AF ∥ 平面 PEC. - 27 - 考点 1 考点 2 考点 3 又 ∵ ∠ DAB= 45 ° , ∴ AB ⊥ DE. 又 ∵ PD ⊥ 平面 ABCD , ∴ PD ⊥ AB. 又 ∵ PD ∩ DE=D , ∴ AB ⊥ 平面 PDE. ∵ AB ⊂ 平面 PAB , ∴ 平面 PED ⊥ 平面 PAB. - 28 - 考点 1 考点 2 考点 3 考向三 　 折叠问题中的平行与垂直关系 例 5 如 图 , 菱形 ABCD 的对角线 AC 与 BD 交于点 O , 点 E , F 分别在 AD , CD 上 , AE=CF , EF 交 BD 于点 H. 将 △ DEF 沿 EF 折到 △ D'EF 的位置 . (1 ) 证明 : AC ⊥ HD' ; 思考 折叠问题的处理关键是什么 ? - 29 - 考点 1 考点 2 考点 3 - 30 - 考点 1 考点 2 考点 3 - 31 - 考点 1 考点 2 考点 3 解题心得 平行与垂直的综合应用问题的主要数学思想方法和处理策略 : (1) 处理平行与垂直的综合问题的主要数学思想是转化 , 要熟练掌握线线、线面、面面之间的平行与垂直的转化 . (2) 探索性问题一般是先根据条件猜测点的位置再给出证明 , 探索点的存在问题 , 点多为中点或三等分点中的某一个 , 也可以根据相似知识找点 . (3) 折叠问题中的平行与垂直关系的处理关键是结合图形弄清折叠前后变与不变的数量关系 , 尤其是隐含着的垂直关系 . - 32 - 考点 1 考点 2 考点 3 对点训练 3 (1) 在三棱锥 P-ABC 中 , △ PAC 和 △ PBC 都是边长为 的等边三角形 , AB= 2, O , D 分别是 AB , PB 的中点 . ① 求证 : OD ∥ 平面 PAC ; ② 求证 : OP ⊥ 平面 ABC ; ③ 求三棱锥 D-ABC 的体积 .