- 2021-06-11 发布 |
- 37.5 KB |
- 5页

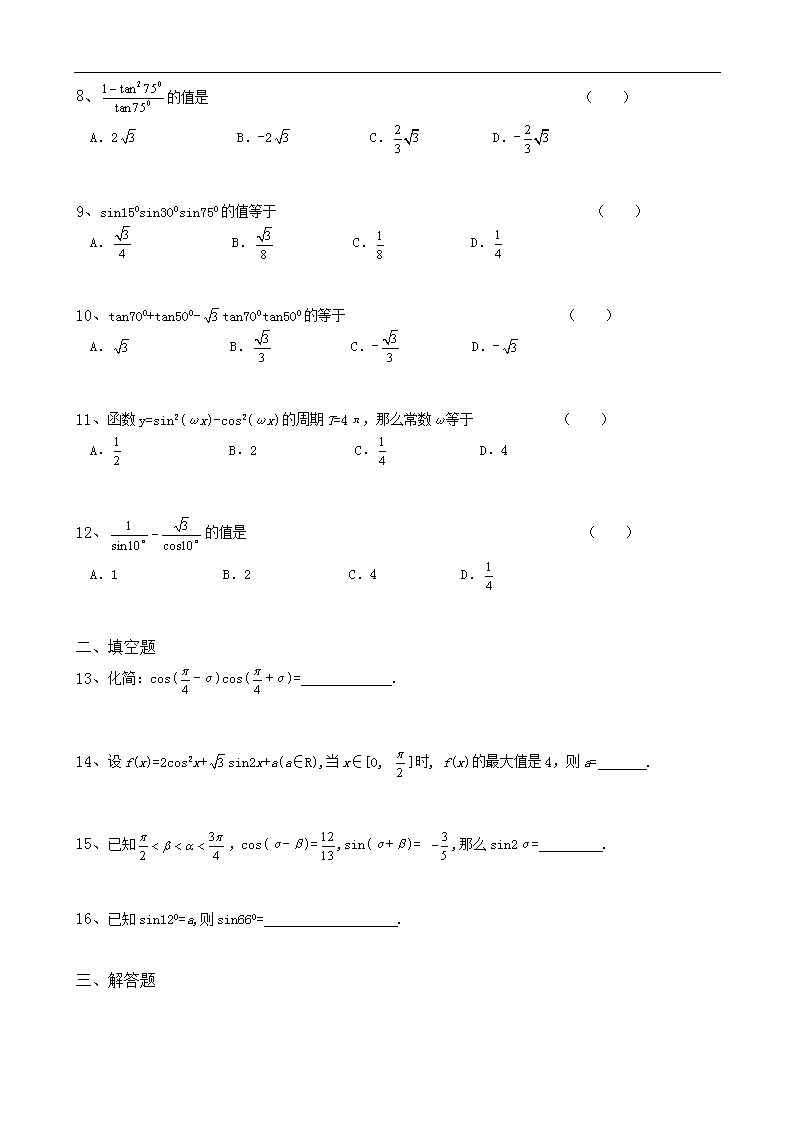

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:三角恒等变换
高三数学 三角恒等变换 一、选择题 1、已知tan(α+β)=,tan(β-)=,则tan(α+)等于 ( ) A. B. C. D. 2、已知sin=,cos=,则角θ所在的的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3、函数y=cos()-sin()的单调递增区间是 ( ) A.[4kπ-, 4kπ-] (k∈Z) B.[4kπ-, 4kπ+] (k∈Z) C.[2kπ-, 2kπ+] (k∈Z) D.[2kπ, 2kπ+π] (k∈Z) 4、已知sinα=,则cos4α的值是 ( ) A. B. C. D. 5、已知sin(α-β)=,sin(α+β)=,且α-β∈(,π), α+β∈(,2π),则cos2β的值是 ( ) A. B. C.1 D.-1 6、△ABC三内角满足2cosBsinA=sinC,则△ABC的形状为 ( ) A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形 7、函数y=sinx+cosx(0≤x≤)的值域是 ( ) A.[] B.[] C.[] D.[] 8、的值是 ( ) A.2 B.-2 C. D.- 9、sin150sin300sin750的值等于 ( ) A. B. C. D. 10、tan700+tan500-tan700tan500的等于 ( ) A. B. C.- D.- 11、函数y=sin2(ωx)-cos2(ωx)的周期T=4π,那么常数ω等于 ( ) A. B.2 C. D.4 12、的值是 ( ) A.1 B.2 C.4 D. 二、填空题 13、化简:cos(-α)cos(+α)= . 14、设f(x)=2cos2x+sin2x+a(a∈R),当x∈[0, ]时, f(x)的最大值是4,则a= . 15、已知,cos(α-β)=,sin(α+β)= ,那么sin2α= . 16、已知sin120=a,则sin660= . 三、解答题 17、已知tanθ=2,求的值. 18、已知向量=(cosα,sinα), =(-sin(α+),cos(α+)),其中O为原点,实数λ满足|λ-|≥||,求实数λ的取值范围. 19、若A、B、C是△ABC的内角,cosB=, sinC=,求cosA的值. 20、已知sin(-θ)= -,<θ<,求cos2θ的值。 21、已知sin(2α+β)=3sinβ,求的值. 22、求y=sinxcosx-cos2x的最大值. 以下是答案 一、选择题 1、C 2、C 3、A 4、B 5、D 6、A; 7、B 8、B 9、C 10、D; 11、C 12、C 二、填空题 13、cos2α; 14、1 15、; 16、1-2a2; 三、解答题 17、 18、∵λ-=(λcosα+ sin(α+),λsinα- cos(α+)) ∴|λ-|= = ==. 由已知得:||=1,又∵|λ-|≥||,∴λ2+λ-2≥0,∴λ≥1或λ≤ -2. 19、cosA = .(提示:若cos C=,则sinA<0) 20、sinθ=sin[-(-θ)]=,故cos2θ= 21、2α+β=(α+β)+ α, β=(α+β)- α,答案为2 22、y=sin(2x-)-,ymax=查看更多