2019学年高二数学上学期期末考试试题 文新 人教
2019学年第一学期期末测试卷
班级________ 姓名_______________ 考场____________ 考号________
高 二 数 学(文科)
一.选择题: (每小题5分,共60分)
1. 椭圆的焦点坐标是( )
A.(0,±6) B.(0,±8) C.(±6,0) D. (±8,0)
2. ( ) 条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
3.不等式的解集是( )
A.{x|x<1或x>4} B.{x|1
2”是“x2-3x+2>0”的充分不必要条件
8.若x,y满足约束条件, 则z=2x+y的最大值是( )
A.3 B.0 C. D.
- 7 -
9.若抛物线上一点到准线的距离等于它到顶点的距离,则点的坐标为( )
A. B. C. D.
10.双曲线的渐近线方程为,焦距为,则双曲线的方程为( )
A. B. C.或 D.以上都不对
11.下列不等式一定成立的是( )
A.lg(x2+)>lgx(x>0) B.sinx+≥2(x≠kπ,k∈Z)
C.x2+1≥2|x|(x∈R) D.>1(x∈R)
12.(如图),F1,F2分别为椭圆的左、右焦点,椭圆上点M的横坐标等于右焦点的横坐标,其纵坐标等于短半轴长的,则椭圆的离心率为( )
A. B.
C. D.
二.填空题: (每小题5分,共20分)
13. 命题“存在,使得”的否定是
14. 若数列的前项和,则通项公式=___ _ ___.
15.双曲线虚轴的一个端点为,两个焦点为,,则双曲线的离心率为 .
16.若对任意x>0,≤a恒成立,则实数a的取值范围是________.
三.解答题(共70分)
17.(10分)根据下列条件,求曲线的标准方程.
(1) 椭圆两个焦点的坐标分别是(-4,0),(4,0),且;
(2)双曲线的离心率e=,经过点(-5,3).
- 7 -
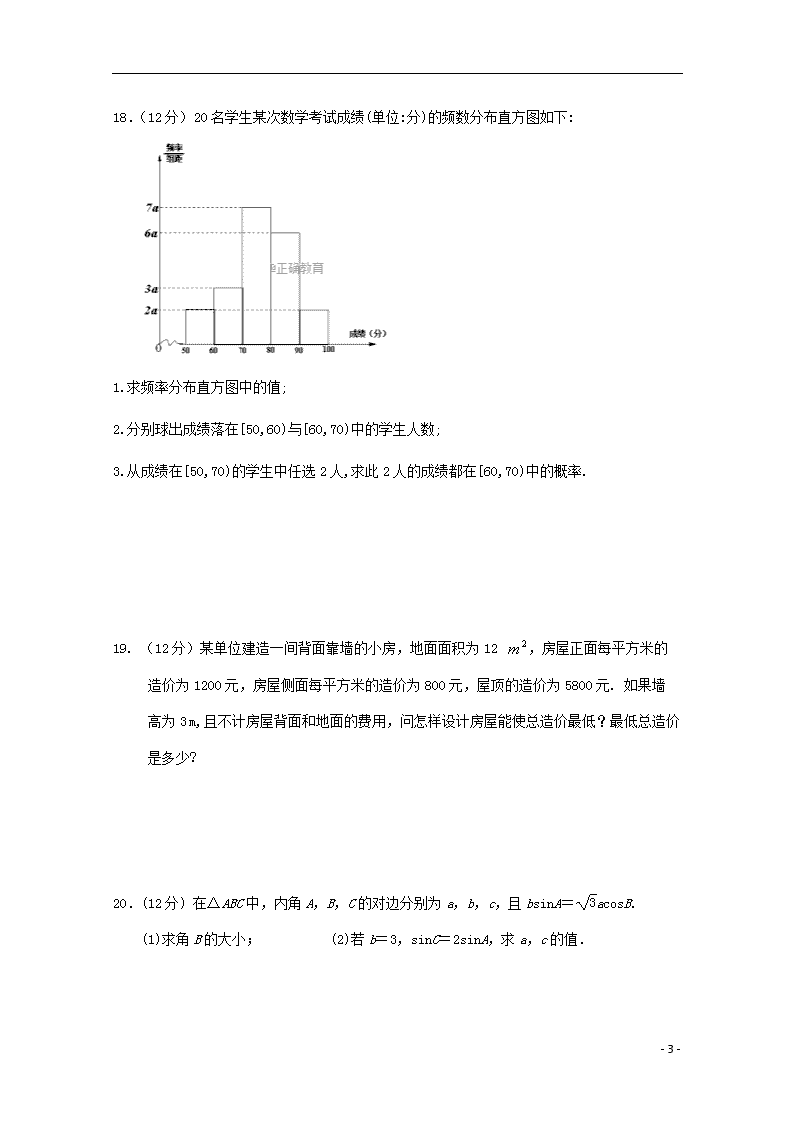
18.(12分)20名学生某次数学考试成绩(单位:分)的频数分布直方图如下:
1.求频率分布直方图中的值;
2.分别球出成绩落在[50,60)与[60,70)中的学生人数;
3.从成绩在[50,70)的学生中任选2人,求此2人的成绩都在[60,70)中的概率.
19. (12分)某单位建造一间背面靠墙的小房,地面面积为12 ,房屋正面每平方米的
造价为1200元,房屋侧面每平方米的造价为800元,屋顶的造价为5800元. 如果墙
高为3 m, 且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低总造价是多少?
20.(12分) 在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=acosB.
(1)求角B的大小; (2)若b=3,sinC=2sinA,求a,c的值.
- 7 -
21.(12分) 数列是等差数列且=1,=5;数列{bn}是正项等比数列,且b1=2,b2+b3=12.
(1)求数列{},{ bn }的通项公式; (2)求数列{}的前n项和Tn.
22.(12分)已知焦点在y轴,顶点在原点的抛物线经过点P(2,2),以上一点为圆心的圆过定点(0,1),记为圆与轴的两个交点.
(1)求抛物线的方程;
(2)当圆心在抛物线上运动时,试判断是否为一定值?请证明你的结论;
(3)当圆心在抛物线上运动时,记,,求的最大值.
- 7 -
高二文答案
一.选择 DABBC DCAAC CD
二.填空
13. 使得 14.
15. 16.
三.解答题
17. (1) ; (2)
18. 1.据题中直方图知组距,由,解得.
2.成绩落在中的学生人数为.
成绩落在中的学生人数为.
3.记成绩落在中的人为,成绩落在中的人为,则从成绩在的学生中任选人的基本事件共有个:,
其中人的成绩都在中的基本事件有个:,故所求概率为.
19. 解:设房屋正面地面的边长为x m , 侧面地面的边长为y m , 总造价为z 元,则
当时,即x=3时,z有最小值,最低总造价为34600元.
- 7 -
20. [解析] (1)由bsinA=acosB及正弦定理=,得sinB=cosB,
所以tanB=,所以B=.
(2)由sinC=2sinA及=,得c=2a.由b=3及余弦定理b2=a2+c2-2accosB,
得9=a2+c2-ac. 所以a=,c=2.
21.
22. (1)由已知,设抛物线方程为,,解得.
所求抛物线的方程为.
(2)法1:设圆心,则圆的半径=
圆C2的方程为.
令,得,得.
(定值).
- 7 -
法2:设圆心,因为圆过,所以半径=,
因为在抛物线上,,且圆被轴截得的弦长
=(定值)
(3)由(2)知,不妨设,
- 7 -