数学理卷·2018届安徽省舒城一中高三寒假模拟（一）（2018

数学理卷·2018届安徽省舒城一中高三寒假模拟（一）（2018

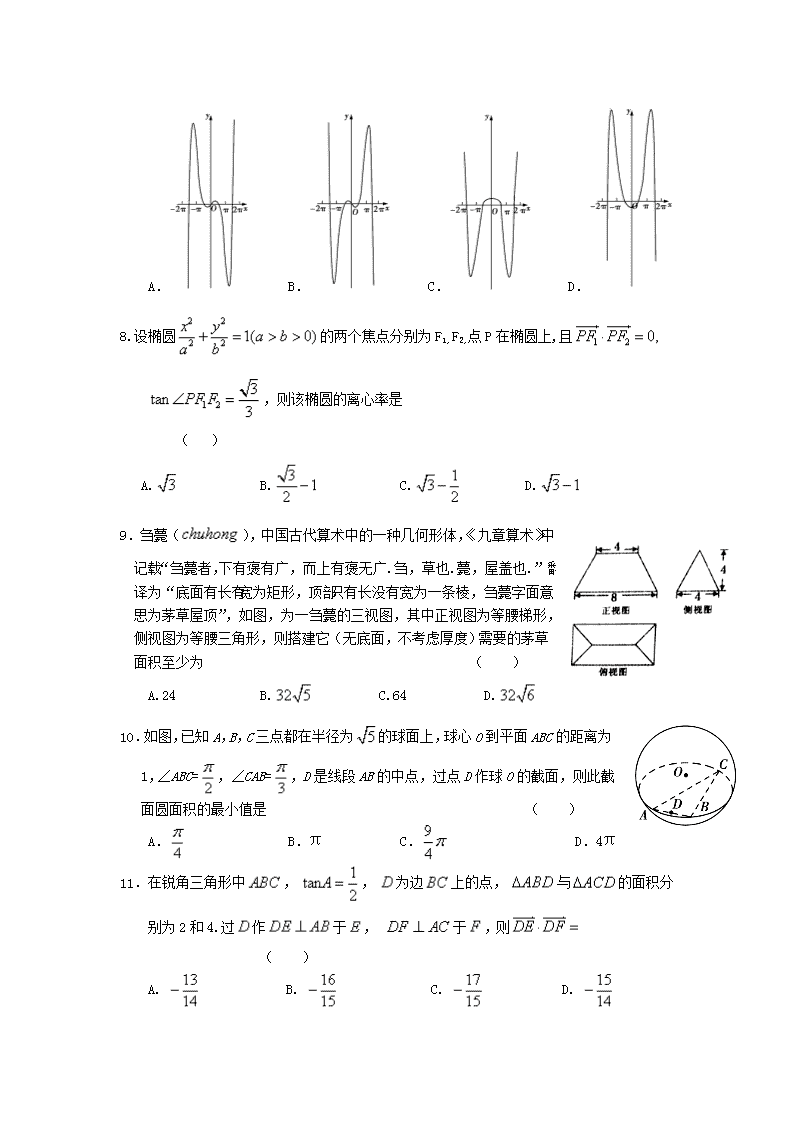
‎2018届高三数学（理）寒假模拟（一）‎ 一、选择题（本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求的．）‎ ‎1．已知集合， ，则 （ ）‎ A. (0,1) B. (0,2] C. [2,4) D. (1,2]‎ ‎2．已知复数，则 （ ）‎ A. B. C. D. ‎ ‎3．设， 是非零向量，则“存在负数，使得”是“”的 （ ）‎ A. 充分而不必要条件 B. 必要而不充分条件 ‎ C. 充分必要条件 D. 既不充分也不必要条件 ‎4．若点在直线上，则的值等于 （ ）‎ A. B. C. D. ‎ ‎5．已知等差数列满足，且， ， 成等比数列，则 （ ）‎ A. 5 B. 3 C. 5或3 D. 4或3‎ ‎6．设随机变量ξ服从正态分布，则函数不存在零点的概率为 （ ）‎ A． B． C． D．‎ ‎7．函数=在[−2π，2π]上的大致图象是 （ ）‎ A． B． C． D．‎ ‎8.设椭圆的两个焦点分别为F1,F2,点P在椭圆上,且 ‎ ，则该椭圆的离心率是 （ ）‎ ‎ A. B. C. D.‎ ‎9．刍薨（），中国古代算术中的一种几何形体，《九章算术》中记载“刍薨者，下有褒有广，而上有褒无广.刍，草也.薨，屋盖也.”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱，刍薨字面意思为茅草屋顶”，如图，为一刍薨的三视图，其中正视图为等腰梯形，侧视图为等腰三角形，则搭建它（无底面，不考虑厚度）需要的茅草面积至少为 （ ）‎ ‎ A.24 B. C.64 D.‎ ‎10．如图，已知A，B，C三点都在半径为的球面上，球心O到平面ABC的距离为1，∠ABC=，∠CAB=，D是线段AB的中点，过点D作球O的截面，则此截面圆面积的最小值是 （ ）‎ A． B．π C． D．4π ‎11．在锐角三角形中， ， 为边上的点， 与的面积分别为2和4.过作于， 于，则 （ ）‎ A. B. C. D. ‎ ‎12．已知当时，函数的图象与 的图象有且只有一个交点，则 正实数m的取值范围是 （ ）‎ A. B. ‎ C. D. ‎ 二、填空题（本题共4小题，每小题5分，共20分．）‎ ‎13．若 展开式中的常数项为 ．‎ ‎14．设满足约束条件，则目标函数的最大值 为5，则 满足的关系为 ；的最小值为 ．‎ ‎15．已知为抛物线： 的焦点，过作斜率为1的直线交抛物线于、两点，设，则__________．‎ ‎16．如图，为了测量河对岸、两点之间的距离，观察者找到一个点，从点可以观察到点、；找到一个点，从点可以观察到点、；找到一个点，从点可以观察到点、；并测量得到一些数据： ， ， ， ， ， ， ，则、‎ 两点之间的距离为__________．（其中取近似值）‎ 三、解答题（本大题共70分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（本小题满分12分）已知为等差数列，前项和为，是首项为2 的等比数列， 且公比大于0， ， ， .‎ ‎（1）求和的通项公式； （2）求数列的前项和.‎ ‎18．(本小题满分12分)如图，三棱台中， 侧面与侧面是 全等的梯形， 若,且.‎ ‎（1）若，，证明：∥平面；‎ ‎（2）若二面角为，求平面与平面所成的锐二面角的余弦值. ‎ ‎19．（本小题满分12分）汽车店是一种以“四位一体”为核心的特许经营模式，包括整车销售、零 配件销售、售后服务、信息反馈等.某品牌汽车店为了了解，，‎ 三种类型汽车质量问题, 对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1.‎ ‎（1）某公司一次性从店购买该品牌，，型汽车各一辆,记表示这三辆车的一年内需要维修 的车辆数，求的分布列及数学期望.(各型汽车维修的频率视为其需要维修的概率).‎ ‎（2）该品牌汽车店为了对厂家新研发的一种产品进行合理定价，将该产品按使事先拟定的各种价格 进行试销相等时间，得到数据如表2.‎ 预计在今后的销售中,销量与单价仍然服从的关系,且该产品的成本是500元/件,为使4S店获得最大利润(利润=销售收入-成本)，该产品 的单价应定位多少元？‎ 表1‎ 车型 ‎ ‎ ‎ ‎ ‎ ‎ 频数 ‎20‎ ‎20‎ ‎40‎ 表2‎ 单价 (元)‎ ‎800‎ ‎820‎ ‎840‎ ‎850‎ ‎880‎ ‎900‎ 销量 (件)‎ ‎90‎ ‎84‎ ‎83‎ ‎80‎ ‎75‎ ‎68‎ ‎20．（本小题满分12分）已知点（2,3）在椭圆上，设， ， 分别为椭 圆的左顶点、上顶点、下顶点、且点到直线的距离为.‎ ‎（1）求椭圆的方程； （2）设， 为椭圆上的两点，且满足 ，求证： 的面积为定值，并求出这个定值.‎ ‎21．（本小题满分12分）已知函数(a∈R)．‎ ‎（1）若a>0，求函数的极值点；‎ ‎（2）若>0对任意的x∈(1，+∞)恒成立，求实数a的取值范围．‎ ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 以直角坐标系的原点为极点，轴的正半轴为极轴建立坐标系，已知点的直角坐标为，若直线的极坐标方程为.曲线的参数方程是（为参数）.‎ （1） 求直线和曲线的普通方程；‎ ‎（2）设直线和曲线交于两点，求.‎ 23． ‎（本小题满分10分）选修4-5：不等式选讲 已知函数.‎ （1） 解不等式；‎ ‎（2）记函数的值域为，若，证明： .‎ 模拟（一） 1.D 2.D 3.A 4.B 5.C 6.A 7.A 8.D 9.B 10.B 11.B 12.A 13.60 14. 15. 16.‎ ‎17．【解析】（1）设等差数列的公差为，等比数列的公比为.由已知，得，而，所有.又因为，解得.所以， .由，可得①. 由，可得②.‎ 联立①②，解得， ，由此可见.所以，数列的通项公式为，数列的通项公式为.‎ 18． ‎【解析】（1）证明：连接，梯形，,易知：，又，则∥，平面，‎ 平面，可得：∥平面；‎ （2） 侧面是梯形，，,,则为二面角的平面角， 均为正三角形，在平面内，过点作的垂线，如图建立空间直角坐标系，不妨设，则,故点，‎ ‎……9分；设平面的法向量为，则有：‎ 设平面的法向量为，则有：，故平面与平面所成的锐二面角的余弦值为.‎ ‎19．【解析】(1)根据表格, 型车维修的概率为, 型车维修的概率为, 型车维修的概率为.‎ 由题意, 的可能值为0,1,2,3,‎ 所以 ； ‎ ‎； ‎ 所以ξ的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎ ‎ 所以 .‎ (2) 设获得的利润为元,根据计算可得, , ，代入回归方程得 ,所 以 ，此函数图象为开口向下,以 为对称轴的抛物线，所以当时, 取的最大值，即为使店获得 最大利润,该产品的单价应定为875元.‎ ‎20．【解析】（1）由题意，得直线的方程为，点，‎ 点到直线的距离 ，整理，得.①‎ 又点在椭圆上， .②‎ 联立①②解得， ，椭圆的方程为.‎ ‎（2）设直线的方程为，代入椭圆方程，并整理得 .‎ ‎ ， ，‎ ‎， ，‎ ‎ .‎ 又，则由题意，得 .‎ 整理，得，则 ，整理，得 ‎（满足）.‎ ‎ ‎ ‎ .又点到直线的距离.‎ ‎ ，为定值.‎ ‎21．【解析】（1）函数的定义域为(0，+∞)，．‎ 令=0，则，Δ=，‎ 当Δ„0，即00，即a>2时，方程有两根，=，=，‎ 显然0<<，‎ 当x∈(0，)时，>0，函数单调递增；‎ 当x∈(，)时，<0，函数单调递减；‎ 当x∈(，+∞)时，>0，函数单调递增．‎ 所以函数的极大值点为=，极小值点为=．‎ 综上，当02时，函数的极大值点为=，‎ 极小值点为=．‎ ‎（2）>0，即>−+2lnx，‎ 所以a>−+对任意的x∈(1，+∞)恒成立，‎ 记=−+，则=−2x+．‎ 设=，则当x>1时，<0，‎ 所以函数在(1，+∞)上单调递减，‎ 所以当x>1时，<=−2×+2−2ln1=0，故<0在x∈(1，+∞)上恒成立，‎ 所以函数=−+在(1，+∞)上单调递减，‎ 所以当x>1时，<=−+=−1，所以a…−1．‎ 所以实数a的取值范围是[−1，+∞)．‎ 22． ‎【解析】（1）因为，所以，由 ，得，因为，消去得，‎ 所以直线和曲线的普通方程分别为和．‎ ‎（2）点的直角坐标为，点在直线上，设直线的参数方程： （为参数）， 对应的参数为． ， ， ，‎ ‎．‎ 23． ‎【解析】‎ 22． ‎（2），当且仅当 时，取等号，∴.原不等式等价于 .‎ ‎∵，∴， .∴.∴.‎