- 2021-06-11 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湖南省郴州市2021届高三数学上学期第二次质检试题(Word版附答案)
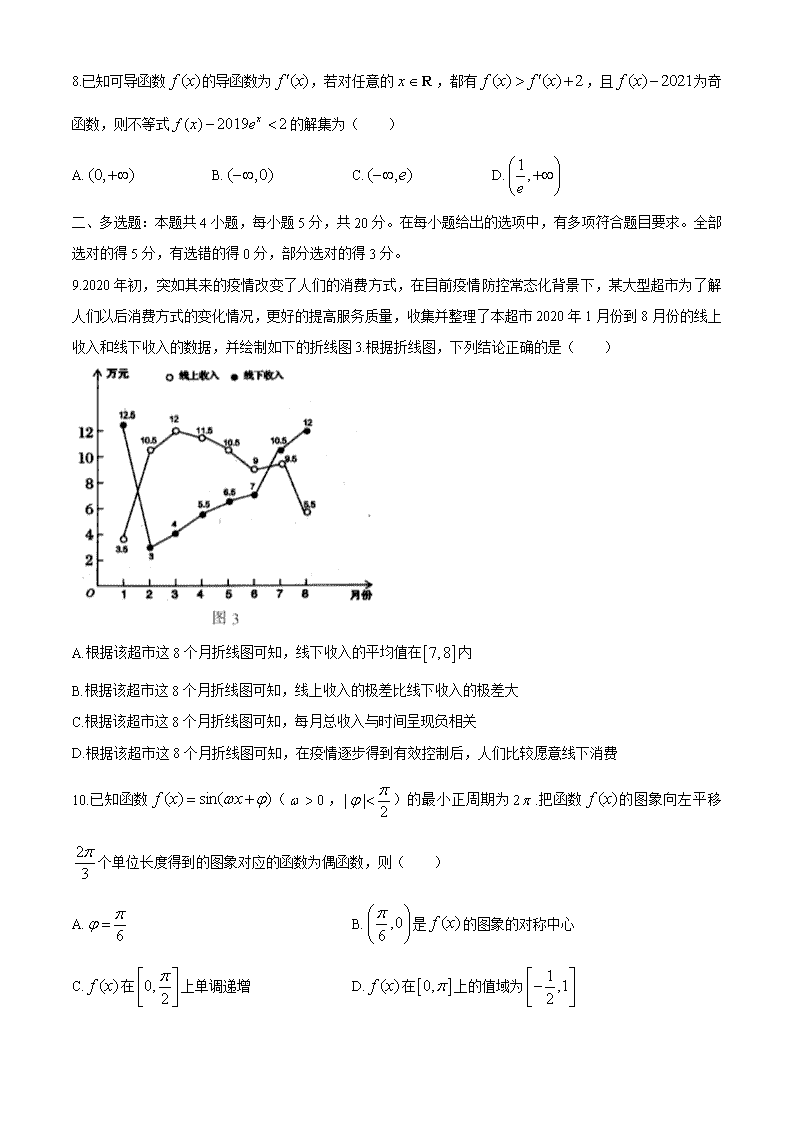
郴州市 2021 届高三上学期第二次质检 数学 (试题卷) 注意事项: 1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真核对条 形码上的姓名、准考证号和科目。 2.学生作答时,选择题和非选择题均须作在答题卡上,在本试题卷上作答无效。考生在答题卡 上按答题卡中注意事项的要求答题。 3.考试结束后,将本试题卷和答题卡一并交回。 4.本试题卷共 5 页。如缺页,考生须声明,否则后果自负。 绝密★启用前 郴州市 2021 届高三第二次教学质量监测试卷 数学 一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要 求的。 1.设集合 2| 2 3 0A x x x , { | 2 3}B x x ,则 A B ( ) A. 1,3 B. 1,3 C. 1,2 D. 2,3 2.若复数 Z 满足 (1 ) 2Z i i ,则下列说法正确的是( ) A. Z 的虚部为 i B. Z 的共轭复数为 1Z i C. Z 对应的点在第二象限 D. 2Z 3.已知 a,b 是两条不同的直线,α,β是两个不同的平面,且 a ,b ,则“ //a b ”是“ // ”的 ( ) A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件 4.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深 奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图 1 所示,一与六共 宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈数为阳数,黑 点数为阴数,若从阳数和阴数中各取一数,则其差的绝对值大于 5 的概率为( ) A. 4 25 B. 7 25 C. 8 25 D. 2 5 5.已知单位向量 a ,满足等式 2| | | |a b ,| 2 | 13a b ,则 a 与b 的夹角为( ) A.120° B.90° C.60° D.30° 6.随着科学技术的发展,放射性同位素技术已经广泛应用于医学、航天等众多领域,并取得了显著经济效益. 假设在放射性同位素钍 234 的衰变过程中,其含量 N(单位:贝克)与时间 t(单位:天)满足函数关系 24 0( ) 2 t N t N ,其中 0N 为 0t 时钍 234 的含量.已知 24t 时,钍 234 含量的瞬时变化率为 8ln 2 ,则 (96)N ( ) A.12 贝克 B.12ln 2 贝克 C.24 贝克 D. 24ln2贝克 7.如图 2,设椭圆 1C : 2 2 2 2 1x y a b ( 0a b )与双曲线 2C : 2 2 2 2 1x y m n ( 0m , 0n )的公共焦 点为 1F , 2F ,将 1C , 2C 的离心率分别记为 1e , 2e ,点 A 是 1C , 2C 在第一象限的公共点,若点 A 关于 2C 的一条渐近线的对称点为 1F ,则 2 2 1 2 2 2 e e ( ) A.2 B. 5 2 C. 7 2 D.4 8.已知可导函数 ( )f x 的导函数为 ( )f x ,若对任意的 x R ,都有 ( ) ( ) 2f x f x ,且 ( ) 2021f x 为奇 函数,则不等式 ( ) 2019 2xf x e 的解集为( ) A. (0, ) B. ( ,0) C. ( , )e D. 1,e 二、多选题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的选项中,有多项符合题目要求。全部 选对的得 5 分,有选错的得 0 分,部分选对的得 3 分。 9.2020 年初,突如其来的疫情改变了人们的消费方式,在目前疫情防控常态化背景下,某大型超市为了解 人们以后消费方式的变化情况,更好的提高服务质量,收集并整理了本超市 2020 年 1 月份到 8 月份的线上 收入和线下收入的数据,并绘制如下的折线图 3.根据折线图,下列结论正确的是( ) A.根据该超市这 8 个月折线图可知,线下收入的平均值在 7,8 内 B.根据该超市这 8 个月折线图可知,线上收入的极差比线下收入的极差大 C.根据该超市这 8 个月折线图可知,每月总收入与时间呈现负相关 D.根据该超市这 8 个月折线图可知,在疫情逐步得到有效控制后,人们比较愿意线下消费 10.已知函数 ( ) sin( )f x x ( 0 ,| | 2 )的最小正周期为 2 .把函数 ( )f x 的图象向左平移 2 3 个单位长度得到的图象对应的函数为偶函数,则( ) A. 6 B. ,06 是 ( )f x 的图象的对称中心 C. ( )f x 在 0, 2 上单调递增 D. ( )f x 在 0, 上的值域为 1 ,12 11.已知抛物线 C: 2 4y x 的焦点为 F, 1 1,P x y , 2 2,Q x y 是抛物线上两点,则下列结论正确的是( ) A. C 的准线方程: 1x B.若直线 PQ过点 F,则 1 2 4x x C.若 5| | | | 2PF QF ,则线段 PQ的中点 M 到 y 轴的距离为 1 4 D.若 PF QF ,则 2OPQS △ 12.已知5 3a ,8 5b ,则( ) A. a b B. 1 1 2a b C. 1 1a ba b D. b aa a b b 三、填空题:本题共 4 小题,每小题 5 分,第 15 题第一问 2 分,第 2 问 3 分,共 20 分。 13. tan 765 __________. 14.已知圆 O 的半径为 5, 4OP ,过点 P 的 2021 条弦的长度组成一个等差数列 na ,最短弦长为 1a ,最 长弦长为 2021a ,则公差 d __________. 15.定义:在等式中 2 0 2 1 2 1 2 2 2 2 1 22 n n n n n n n n n n nx x D x D x D x D x D ( *n N )中,把 0 nD , 1 nD , 2 nD ,… 2n nD 叫做三项式 2 2 n x x 的 n 次系数列(如三项式的 1 次系数列是 1,-1,-2).则(1)三项 式 2 2 n x x 的 2 次系数列各项之和等于__________;(2) 9 5D __________. 16.如图 4,已知球 O 是直三棱柱 1 1 1ABC A B C 的外接球, 1 6AC BC CC , AC BC ,E,F 分别 为 1BB , 1 1AC 的中点,过点 A,E,F 作三棱柱的截面α,若α交 1 1B C 于 M,过点 M 作球 O 的截面,则所得 截面圆面积的最小值是__________. 四、解答题:本大题共 6 小题,共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.(本小题满分 10 分) 设 na 为等差数列, nb 是正项等比数列,且 1 1 2a b , 3 22a b .在① 5 3 112b b b ,② 5 42a b , ③ 2 2 1log log 1n nb b , 2n , *n N 这三个条件中任选一个,求解下列问题: (Ⅰ)写出你选择的条件并求数列 na 和 nb 的通项公式; (Ⅱ)在(Ⅰ)的条件下,若 n n nc a b ( *n N ),求数列 nc 的前 n 项和 nS . 18.(本小题满分 12 分) 如图 5,在平面四边形 ABCD 中, AB AD , 1AB , 3AD , 2BC . (I)若 2 2CD ,求四边形 ABCD 的面积; (Ⅱ)若 7cos 5BCD , 0, 2ADC ,求 sin ADC . 19.(本小题满分 12 分) 如图 6,在直四棱柱 1 1 1 1ABCD A B C D 中,四边形 ABCD 为平行四边形,M 为 1AA 的中点, 1BC BD , 1 2AB AA . (Ⅰ)求证:平面 BMD 平面 BDC ; (Ⅱ)求二面角 1 1D MC C 的正弦值. 20.(本小题满分 12 分) 已知椭圆 C: 2 2 2 2 1x y a b ( 0a b )的离心率为 3 3 ,直线 5 0x y 与椭圆 C 有且只有一个公共 点. (Ⅰ)求椭圆 C 的标准方程 (Ⅱ)设点 ( 3,0)A , ( 3,0)B ,P 为椭圆 C 上一点,且直线 PA 与 PB 的斜率乘积为 2 3 ,点 M,N 是椭圆 C 上不同于 A,B 的两点,且满足 //AP OM , //BP ON ,求证: OMN△ 的面积为定值. 21.(本小题满分 12 分) 已知函数 ( ) 1 lnxf x ae x (Ⅰ)当 1a ,讨论函数 ( )f x 的单调性; (Ⅱ)若不等式 ( ) x af x e x x ( 0a ),对 (1, )x 恒成立,求实数 a 的取值范围. 22.(本小题满分 12 分) 垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列 活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.垃圾分类后,大部分运往垃圾处 理厂进行处理.为了监测垃圾处理过程中对环境造成的影响,某大型垃圾处理厂为此建立了 5 套环境监测系 统,并制定如下方案:每年工厂的环境监测费用预算定为 80 万元,日常全天候开启 3 套环境监测系统,若 至少有 2 套系统监测出排放超标,则立即检查污染处理系统;若有且只有 1 套系统监测出排放超标,则立 即同时启动另外 2 套系统进行 1 小时的监测,且后启动的这 2 套监测系统中只要有 1 套系统监测出排放超 标,也立即检查污染处理系统.设每个时间段(以 1 小时为计量单位)被每套系统监测出排放超标的概率均 为 p( 0 1p ),且各个时间段每套系统监测出排放超标情况相互独立. (Ⅰ)当 1 2p 时,求某个时间段需要检查污染处理系统的概率; (Ⅱ)若每套环境监测系统运行成本为 20 元/小时(不启动则不产生运行费用),除运行费用外,所有的环 境监测系统每年的维修和保养费用需要 6 万元.现以此方案实施,问该工厂的环境监测费用是否会超过预算 (全年按 9000 小时计算)?并说明理由. 郴州市 2021 届高三第二次教学质量监测试卷 数学参考答案及评分细则 一、选择题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要 求的。 1-5 BCDAC 6-8 CDA 二、多选题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的四个选项中,多项是符合题目要求的。 全部选对得 5 分,有选错得 0 分,部分选对得 3 分。 9.AD 10.BCD 11.ACD 12.ABD 三、填空题:本题共 4 小题,每小题 5 分,第 16 题第一问 2 分,第 2 问 3 分,共 20 分。 13.1 14. 1 505 15.(1)4 (2)-80 16.8 四、解答题:本大题共 6 小题,共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.(Ⅰ)选择①:设 na 的公差为 d, nb 的公比为 q( 0q ). 则根据题意有 4 2 2 2 4 2 2 24 d q q q ,·················································································(2 分) 解得 2 3 q d ············································································································· (4 分) 所以, 2 3( 1) 3 1na n n 12 2 2n n nb ·························································(5 分) 选择②:设 na 的公差为 d, nb 的公比为 q( 0q ). 则根据题意有 3 2 2 4 2 4 2 2 d q d q ,··············································································· (2 分) 解得 2 3 q d ············································································································· (4 分) 所以 2 3( 1) 3 1na n n , 12 2 2n n nb .····················································· (5 分 ) 选择③:由 2 2 1log log 1n nb b , 2n , *n N 得 2 2 1log log 1n nb b ∴ 1 2n n b b ·············································································· (2 分) ∴ nb 的公比为 2q 又 2 2 4d q ∴ 3d ·····························································(4 分) 所以 2 3( 1) 3 1na n n , 12 2 2n n nb .··························································· (5 分) (Ⅱ)由(Ⅰ)可知 (3 1) 2n nc n ··········································································· (6 分) 2 32 2 5 2 8 2 (3 1) 2n nS n ① 2 3 12 2 2 5 2 (3 4)2 (3 1)2n n nS n n ②···················································· (7 分) ①-②得 2 3 12 2 3 2 3 2 3 2 (3 1) 2n n nS n ············································(8 分) 2 3 14 3 2 2 2 (3 1)2n nn ········································································ (9 分) ∴ 2 12 2 24 3 (3 1)21 2 n n nS n 1(3 4)2 8nn ··································································································· (10 分) 18.(Ⅰ)连接 BD,在 Rt ABD△ 中 由勾股定理得: 2 2 2 4BD AB AD ,所以 2BD ················································· (1 分) 在 BCD△ 中,由余弦定理知: 2 2 2 3cos 2 4 BC CD BDC BC CD ·····································(3 分) ∴ 2 7sin 1 cos 4C C ··················································································· (4 分) 所以 1 7sin2 2BCDS BC CD C △ , 1 3 2 2ABDS AB AD △ ···································· (5 分) 所以 ABCD 的面积 3 7 2ABD BCDS S S △ △ ························································· (6 分) (Ⅱ)由 7cos 5BCD 得 3 2sin 5BCD ·····························································(7 分) 在 BCD△ 中,由正弦定理知: sin sin BC BD BDC BCD 所以 sin 3sin 5 BC BCDBDC BD ········································································· (8 分) 因为 0, 2ADC ,所以 0, 2BDC , 4cos 5BDC ····································(9 分) 在 Rt ABD△ 中, 3tan 3 ABADB AD ,所以 6ADB ······································(10 分) 所以 3 3 4 1 4 3 3sin sin 6 5 2 5 2 10ADC BDC ·································· (12 分) 19.(Ⅰ)因为 1BC BD , 2CD AB .可得 2 2 2BC BD CD , ∴ BD BC ,又∵ //AD BC ,∴ BD AD . 又∵ 1 1 1 1ABCD A B C D 是直四棱柱, ∴ 1DD 平面 ABCD .∴ 1DD BD . 1DD AD D ,∴ BD 平面 1 1ADD A , ∴ BD MD .·········································································································· (2 分) 法一:取 1BB 中点 N,连接 NC , MN , ∵ //MN DC ,∴四边形 MNCD 为平行四边形,∴ //MD NC , ∵ 1 2 2 NB BC BC CC ,∴ 1NBC BCC∽△ △ ,∴ 1 90C BC BCN ,∴ 1BC CN , 又∵ //MD NC ,∴ 1MD BC .··················································································· (4 分) 又 1BC BD B ,∴ MD 平面 1BDC .······································································(5 分) 又 MD 平面 MBD ,所以平面 BMD 平面 1BDC .······················································ (6 分) 法二:连接 1 1AC ,可计算得 1 22 2C M , 6 2MD , 1 2C D , 所以 2 2 2 1 1MD C D MC ,由勾股定理的逆定理得: 1MD DC ,余同法一 (Ⅱ)以 DA为 x 轴, DB为 y 轴, 1DD 为 z 轴,建立如图所示的坐标系, 则 (0,1,0)B , 1( 1,1, 2)C , 1(0,0, 2)D , 21,0, 2M ∴ 1 22,1, 2MC , 1 (0,0, 2)CC , 1 1 ( 1,1,0)D C ············································ (7 分) 设 平 面 1C CM 的 法 向 量 为 ( , , )n x y z , 由 1 1 0 0 CC n MC n 得 2 0 2 3 0 z x y z 可 求 得 一 个 法 向 量 (1,2,0)n ············································································································· (8 分) 同理可得平面 1 1D C M 的一个法向量 (1,1, 2)m ························································· (10 分) 设二面角 1 1D MC C 的大小为θ 所以 | | 3 3 5| cos | | cos , | | || | 102 5 m nm n m n ·····················································(11 分) 则 55sin 10 ,即二面角 1M BC D 的正弦值为 55 10 .·············································(12 分) 20.解:(Ⅰ)∵直线 5 0x y 与椭圆有且只有一个公共点, ∴直线 5 0x y 与椭圆 C: 2 2 2 2 1x y a b ( 0a b )相切, ∴ 2 2 2 2 5 0 1 x y x y a b 2 2 2 2 2 2 22 5 5 0b a x a x a a b ·········································· (3 分) ∴ 2 20 5a b 又∵ 3 3 c a ,∴ 3a ,∴ 2 2 2 2b a c , 椭圆 C 的方程为 2 2 13 2 x y .······················································································(5 分) (Ⅱ)证明:由题意 M、N 是椭圆 C 上不同于 A,B 的两点, 由题意知,直线 AP , BP 斜率存在且不为 0,又由已知 2 3AP BPk k . 由 //AP OM , //BP ON ,所以 2 3OM ONk k ······························································ (6 分) 设直线 MN 的方程为 x my t , 代入椭圆方程得 2 2 22 3 4 2 6 0m y mty t ①······················································(7 分) 设 1 1,M x y , 2 2,N x y , 则 1 2 2 4 2 3 mty y m , 2 1 2 2 2 6 2 3 ty y m ······································································ (8 分) 又 2 1 2 1 2 2 2 2 2 1 2 1 2 1 2 2 6 2 3 6 3OM ON y y y y tk k x x m y y mt y y t t m ··································· (9 分) 得 2 22 2 3t m ·····································································································(10 分) 所以 2 2 1 2 2 2 1 1 48 24 72 1 2 6 | | 6| | | | | |2 2 2 3 2 2 2MON m t tS t y y t tm t △ 即 MON△ 的面积为定值 6 2 ·················································································(12 分) 21.解:(Ⅰ) ( )f x 的定义域为 (0, ) , 1( ) lnxf x e x x ,······································ (1 分) 令 1( ) lng x x x ,则 2 2 1 1 1( ) xg x x x x ,·····························································(2 分) 当 (0,1)x 时, ( ) 0g x , ( )g x 单调递减, 当 (1, )x 时, ( ) 0g x , ( )g x 单调递增,······························································(3 分) ∴ 1x 时, ( )g x 取得极小值即最小值 (1) 1g , ∴ ( ) 0f x 在 (0, ) 恒成立,·················································································· (4 分) ∴ ( )f x 在 (0, ) 单调递增;····················································································· (5 分) (Ⅱ)不等式 ( ) x af x e x x 等价于 ln ln lnx a x x a ae x x a x e e x x ,····· (6 分) 设 ( ) lnk t t t ,即 x ak e k x (*) ∵ 1 1( ) 1 tk t t t ································································································· (7 分) ∴当 (0,1)t , ( ) 0k t , ( )k t 在 (0,1) 是减函数 (1, )t , ( ) 0k t , ( )k t 在 (1, ) 是增函数 ·························································(8 分) ∵ (1, )x , 10 1xe e ···············································································(9 分) 当 0a 时, 0 1ax ,且 ( )k t 在 (0,1) 是减函数 则(*)式 ln x a xe x a x 令 ( ) ln xh x x ( 1x ),则 2 ln 1( ) (ln ) xh x x ,······························································ (10 分) 当 (1, )x e 时, ( ) 0h x , ( )h x 单调递减, 当 ( , )x e 时, ( ) 0h x , ( )h x 单调递增,····························································(11 分) min( ) ( )h x h e e a e ∴ a e 又 0a ∴ 0e a ································· (12 分) 22.(Ⅰ)设某个时间段在需要开启 3 套系统就被确定需要检查污染源处理系统的事件为 A 2 3 3 3 2 2 3 3 2 3 2 3 3 3 3 3 3 3 1 1 1 1 1 1( ) (1 ) 2 2 2 2 2 2P A C p p C p C C C C ,···············(2 分) 设某个时间段在需要开启另外 2 套系统才能确定需要检查污染源处理系统的事件为 B 3 2 1 2 2 1 3 3 1 1 9( ) (1 ) 1 (1 ) 12 2 32P B C p p p C ···········································(5 分) ∴某个时间段需要检查污染源处理系统的概率为 1 9 25 2 32 32 ··········································· (6 分) (Ⅱ)设某个时间段环境监测系统的运行费用为 X 元,则 X 的可能取值为 60,100.···············(7 分) 1 2 3( 100) (1 )P X C p p 1 2 3( 60) 1 (1 )P X C p p ···············································(8 分) 1 2 1 2 2 3 3( ) 60 1 (1 ) 100 (1 ) 60 120 (1 )E X C p p C p p p p 令 2( ) (1 )g p p p , (0,1)p ,则 2( ) (1 ) 2 (1 ) (3 1)( 1)g p p p p p p .··············(9 分) 当 10, 3p 时, ( ) 0g p , ( )g p 在 10, 3 上单调递增, 当 1,13p 时, ( ) 0g p , ( )g p 在 1,13 上单调递减,············································ (10 分) ∴ ( )g p 的最大值为 1 4 3 27g ,············································································· (11 分) ∴实施此方案,最高费用为 446 9000 60 120 10 7627 (万元), ∵ 76 80 ,故不会超过预算.···················································································· (12 分)查看更多