数学文卷·2018届广东省中山一中（中山市）高二下学期期末考试（2017-07）

数学文卷·2018届广东省中山一中（中山市）高二下学期期末考试（2017-07）

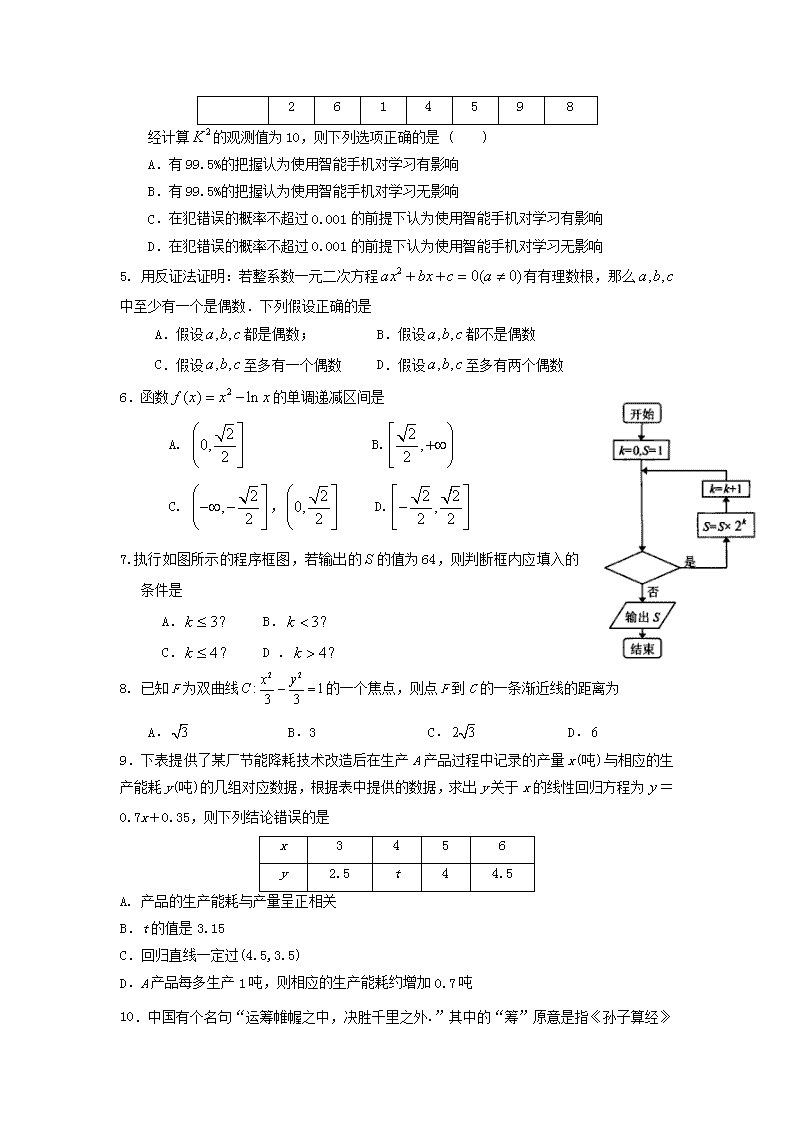
中山市高二级2016—2017学年度第二学期期末统一考试 高二数学试卷（文科）‎ 本试卷共4页，22小题， 满分150分． 考试用时120分钟．‎ 注意事项：‎ ‎1、答卷前，考生务必用2B铅笔在答题卡“考生号”处填涂考生号，用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上．‎ ‎2、选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．‎ ‎3、非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上．如需改动，先划掉原来的答案，然后再写上新的答案．不准使用铅笔和涂改液．不按以上要求作答的答案无效．‎ ‎4、考生必须保持答题卡的整洁．考试结束，将答题卡交回，试卷不用上交．‎ 一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个备选项中，只有一项是符合题目要求的．）‎ ‎1. 抛物线的焦点坐标为 ‎ A． B． C． D．‎ ‎2. 若复数满足，则 A． B． C． D． ‎ ‎3. 命题“R，”的否定为 ‎ A． R， B． R，‎ ‎ C． R， D． R，‎ ‎4．某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：‎ 使用智能手机 不使用智能手机 总计 学习成绩优秀 ‎4‎ ‎8‎ ‎12‎ 学习成绩不优秀 ‎16‎ ‎2‎ ‎18‎ 总计 ‎20‎ ‎10‎ ‎30‎ 附表：‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 经计算的观测值为10，则下列选项正确的是 (　　)‎ A．有99.5%的把握认为使用智能手机对学习有影响 B．有99.5%的把握认为使用智能手机对学习无影响 C．在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响 D．在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响 ‎5. 用反证法证明：若整系数一元二次方程有有理数根，那么中至少有一个是偶数．下列假设正确的是 ‎ A．假设都是偶数； B．假设都不是偶数 ‎ C．假设至多有一个偶数 D．假设至多有两个偶数 ‎6．函数的单调递减区间是 ‎ A. B. ‎ ‎ C. ， D.‎ ‎7.执行如图所示的程序框图，若输出的的值为64，则判断框内应填入的条件是 A． B． ‎ C． D ．‎ ‎8. 已知F为双曲线的一个焦点，则点F到C的一条渐近线的距离为 ‎ A． B．3 C． D．‎ ‎9．下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据，根据表中提供的数据，求出y关于x的线性回归方程为＝0.7x＋0.35，则下列结论错误的是 x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ t ‎4‎ ‎4.5‎ A. 产品的生产能耗与产量呈正相关 ‎ B．t的值是3.15‎ C．回归直线一定过(4.5,3.5) ‎ D．A产品每多生产1吨，则相应的生产能耗约增加0.7吨 ‎10．中国有个名句“运筹帷幄之中，决胜千里之外.”其中的“筹”原意是指《孙子算经》‎ ‎ 中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进 行运算，算筹的摆放形式有纵横两种形式，如下表 表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位 数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位 用横式表示，以此类推， 例如6613用算筹表示就是： ，则9117‎ 用算筹可表示为 A. B． ‎ C． D．‎ ‎11. 设，分别为双曲线：的左右焦点，点关于渐近线的对称点恰好落在以为圆心,为半径圆上,则双曲线的离心率为 A． B． C． D． ‎ ‎12. 大衍数列，来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论．其前10项为：0、2、4、8、12、18、24、32、40、50．通项公式：，如果把这个数列排成如图形状，并记表示第m行中从左向右第n个数，则的值为 A．1200 B．1280 C．3528 D． 3612‎ 二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡相应横线上）‎ ‎13. 一质点做直线运动，它所经过的路程和时间的关系是s=3t2+t，则t=2时的瞬时速度为 . ‎ ‎14. 已知是函数的一个极值点，则实数 ‎ ‎15. 双曲线上一点P到它的一个焦点的距离等于3，那么点P与两个焦点所构 ‎ 成的三角形的周长等于 .‎ ‎16. 已知函数，如果对任意的，都有成立，则实数a的取值范围是 .‎ 三、解答题（本大题共6小题，共70分，解答须写出文字说明、证明过程和演算步骤．）‎ ‎17. （本小题满分10分）已知复数()，且为纯虚数.‎ ‎（1）求复数； （2）若，求复数的模.‎ ‎18.（本小题满分12分）‎ 已知，设：实数满足，：实数满足．‎ ‎（1）若，且为真，求实数的取值范围；‎ ‎（2）若是的充分不必要条件，求实数的取值范围．‎ ‎19.（本小题满分12分）‎ ‎ 为了研究一种昆虫的产卵数和温度是否有关，现收集了7组观测数据列于下表中，并做出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈现线性相关关系，现分别用模型①与模型；②作为产卵数和温度的回归方程来建立两个变量之间的关系.‎ 温度 ‎20‎ ‎22‎ ‎24‎ ‎26‎ ‎28‎ ‎30‎ ‎32‎ 产卵数个 ‎6‎ ‎10‎ ‎21‎ ‎24‎ ‎64‎ ‎113‎ ‎322‎ ‎400‎ ‎484‎ ‎576‎ ‎676‎ ‎784‎ ‎900‎ ‎1024‎ ‎1.79‎ ‎2.30‎ ‎3.04‎ ‎3.18‎ ‎4.16‎ ‎4.73‎ ‎5.77‎ ‎26‎ ‎692‎ ‎80‎ ‎3.57‎ ‎1157.54‎ ‎0.43‎ ‎0.32‎ ‎0.00012‎ 其中，，，，‎ 附：对于一组数据，，……，其回归直线的斜率和截距的最小二乘估计分别为：，‎ ‎（1）根据表中数据，分别建立两个模型下关于的回归方程；并在两个模型下分别估计温度为时的产卵数.（与估计值均精确到小数点后两位）（参考数据：）‎ ‎（2）若模型①、②的相关指数计算分别为，请根据相关指数判断哪个模型的拟合效果更好.‎ ‎20.（本小题满分12分）‎ ‎ 已知椭圆：的右焦点为，右顶点为，设离心率为，且满足，其中为坐标原点．‎ ‎ （1）求椭圆的方程；‎ ‎ （2）过点的直线l与椭圆交于M，N两点，求△OMN面积的最大值．‎ ‎21. （本小题满分12分）‎ ‎ 设函数.‎ ‎ （1）若曲线在点处的切线与直线垂直，求 的单调区间（其中为自然对数的底数）；‎ ‎ （2）若对任意恒成立，求的取值范围. ‎ ‎22. （本小题满分12分）‎ ‎ 对于命题：存在一个常数，使得不等式对任意正数，恒成立.‎ ‎（1）试给出这个常数的值；‎ ‎（2）在（1）所得结论的条件下证明命题； ‎ ‎（3）对于上述命题，某同学正确地猜想了命题：“存在一个常数，使得不等式对任意正数，，恒成立．”观察命题与命题的规律，请猜想与正数，，，相关的命题．‎ 中山市高二级2016—2017学年度第二学期期末统一考试 高二数学试卷（文科）答案 一、选择题： DCDAB AAABA CD 二、填空题：‎ ‎13．13； 15． 12； 15．42； 16．.‎ 三、解答题：‎ ‎17．解: (1) ………………… 2分 ‎∵为纯虚数，∴ ………………… 2分 ‎∴，所以 ………………… 5分 ‎ (2), ………………… 8分 ‎∴. ………………… 10分 ‎18.解：（1）由得 当时，，即为真时实数的取值范围是. …………2分 由，得，即为真时实数的取值范围是.………4分 因为为真，所以真且真，‎ 所以实数的取值范围是. …………6分 (2) ‎ 由得，‎ 所以，为真时实数的取值范围是. …………8分 因为 是的充分不必要条件，即是的充分不必要条件 所以且 …………10分 所以实数的取值范围为：. …………12分 ‎19. 解：（1）对于模型①：设，则 其中， ……………………… 1分 ‎ …………………… 3分 所以， ………………… 4分 当时，估计产卵数为 …… 5分 对于模型②：设，则 ‎ 其中，………………………………… 6分 ‎ ……………………… 8分 所以， ………………………………… 9分 当时，估计产卵数为………… 10分 ‎（2）因为，所以模型②的拟合效果更好 ………………………………… 12分 ‎20.解：（1）设椭圆的焦半距为c，则|OF| = c，|OA| = a，|AF| =．‎ ‎ 所以，其中，又，联立解得，．‎ ‎ 所以椭圆C的方程是． ………………………………………… 4分 ‎（2）由题意直线不能与x轴垂直，否则将无法构成三角形． …………… 5分 ‎ 当直线l与x轴不垂直时，设其斜率为k，那么l的方程为．‎ ‎ 联立l与椭圆C的方程，消去y，得．‎ ‎ Δ=，显然大于0．‎ 设点，．则，． ……… 7分 所以，又O到l的距离．‎ 所以△OMN的面积． ……… 10分 令，那么，当且仅当t = 3时取等．‎ 所以△OMN面积的最大值是． ………………………………… 12分 ‎21.解：（1）由，知，且，……1分 因为曲线在点处的切线与直线垂直，所以，‎ 所以，得， ……3分 所以，‎ 令，得，在上单调递减；‎ 令，得，在上单调递增，‎ 综上，的单调减区间为,单调增区间为. ……5分 ‎（2）因为，恒成立，‎ ‎ 则有，对恒成立， ……7分 ‎ 令，则在上单调递减，‎ ‎ 所以在上恒成立， ……9分 ‎ 所以恒成立， ……10分 ‎ 令，则.‎ ‎ 所以的取值范围是. ……12分 ‎22. 解：（1）令得：，故； ……3分 ‎（2）先证明.‎ ‎ ∵，，要证上式，只要证，‎ ‎ 即证 即证，这显然成立.‎ ‎ ∴. ……6分 ‎ 再证明.‎ ‎ ∵，，要证上式，只要证，‎ ‎ 即证 即证，这显然成立.‎ ‎ ∴. ……9分 ‎ ‎（3）猜想结论：存在一个常数，使得不等式 对任意正数，，，恒成立. ……12分