2012高考试题分类汇编:圆锥曲线
2012高考试题分类汇编:圆锥曲线
一、选择题
1、【2012高考上海文16】对于常数、,“”是“方程的曲线是椭圆”的( )
A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
2、【2102高考福建文5】已知双曲线-=1的右焦点为(3,0),则该双曲线的离心率等于
A B C D
3、【2012高考新课标文4】设是椭圆的左、右焦点,为直线上一点,是底角为的等腰三角形,则的离心率为( )
4、【2012高考江西文8】椭圆的左、右顶点分别是A,B,左、右焦点分别是F1,F2。若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为
A. B. C. D.
5、【2012高考四川文11】方程中的,且互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
A、28条 B、32条 C、36条 D、48条
6、【2012高考四川文9】已知抛物线关于轴对称,它的顶点在坐标原点,并且经过点。若点到该抛物线焦点的距离为,则( )
A、 B、 C、 D、
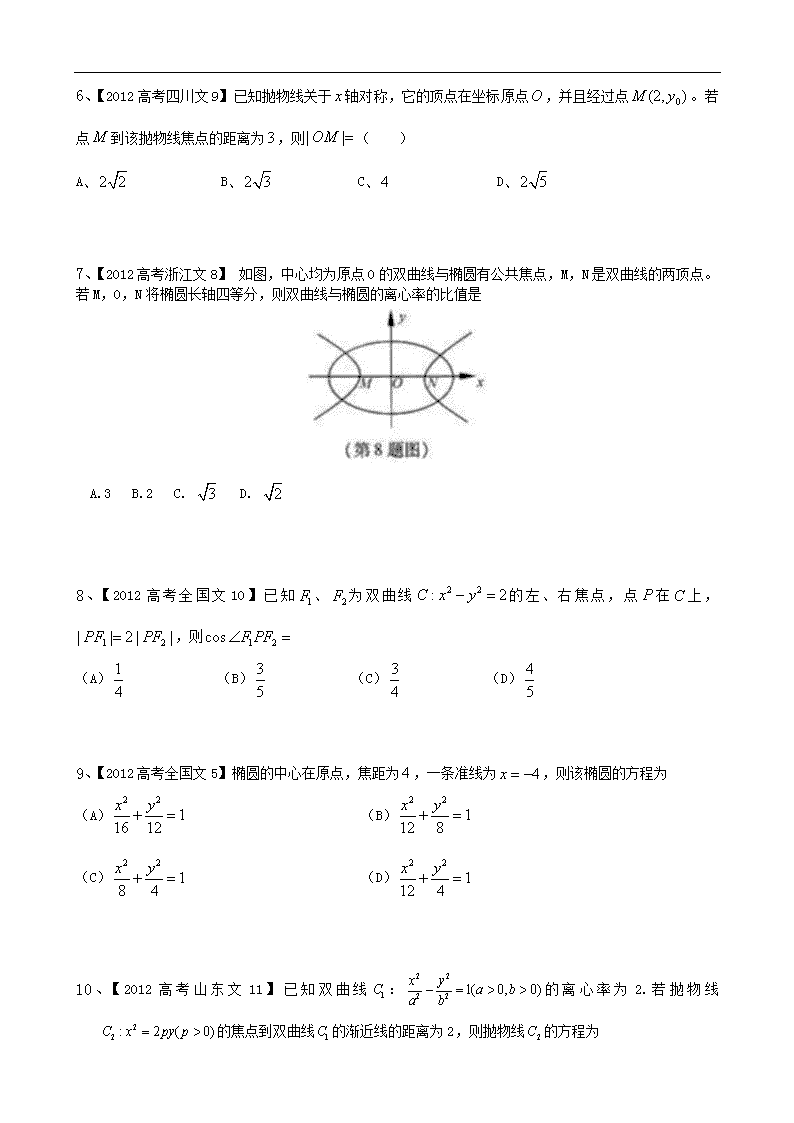
7、【2012高考浙江文8】 如图,中心均为原点O的双曲线与椭圆有公共焦点,M,N是双曲线的两顶点。若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是
A.3 B.2 C. D.
8、【2012高考全国文10】已知、为双曲线的左、右焦点,点在上,,则
(A) (B) (C) (D)
9、【2012高考全国文5】椭圆的中心在原点,焦距为,一条准线为,则该椭圆的方程为
(A) (B)
(C) (D)
10、【2012高考山东文11】已知双曲线:的离心率为2.若抛物线的焦点到双曲线的渐近线的距离为2,则抛物线的方程为
(A) (B) (C) (D)
11、【2012高考新课标文10】等轴双曲线的中心在原点,焦点在轴上,与抛物线的准线交于两点,;则的实轴长为( )
12、【2012高考湖南文6】已知双曲线C :-=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A.-=1 B.-=1 C.-=1 D.-=1[w~#ww.zz&st^ep.com@]
二、填空题
13、【2012高考天津文科11】已知双曲线与双曲线有相同的渐近线,且的右焦点为,则
14、【2012高考四川文15】椭圆为定值,且的的左焦点为,直线与椭圆相交于点、,的周长的最大值是12,则该椭圆的离心率是______。
15、【2012高考辽宁文15】已知双曲线x2 y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥P F2,则∣P F1∣+∣P F2∣的值为___________________.
16、【2012高考江苏8】在平面直角坐标系中,若双曲线的离心率为,则的值为 ▲ .
17、【2012高考陕西文14】右图是抛物线形拱桥,当水面在时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
18、【2012高考重庆文14】设为直线与双曲线 左支的交点,是左焦点,垂直于轴,则双曲线的离心率
19、【2012高考安徽文14】过抛物线的焦点的直线交该抛物线于两点,若,则=______。
三、解答题
20、【2012高考上海文22】在平面直角坐标系中,已知双曲线
(1)设是的左焦点,是右支上一点,若,求点的坐标;
(2)过的左焦点作的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(3)设斜率为()的直线交于、两点,若与圆相切,求证:⊥
21、【2012高考重庆文21】
已知椭圆的中心为原点,长轴在 轴上,上顶点为 ,左、右焦点分别为 ,线段 的中点分别为 ,且△是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过 作直线交椭圆于,,求△的面积
22、【2012高考四川文21】
如图,动点与两定点、构成,且直线的斜率之积为4,设动点的轨迹为。
(Ⅰ)求轨迹的方程;
(Ⅱ)设直线与轴交于点,与轨迹相交于点,且,求的取值范围。
23、【2012高考江西文20】
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2
0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由。
27、【2012高考湖南文21】
在直角坐标系xOy中,已知中心在原点,离心率为的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.[中国教育出%版网^@*&]
(Ⅰ)求椭圆E的方程;
(Ⅱ)设P是椭圆E上一点,过P作两条斜率之积为的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
28、已知椭圆(a>b>0),点P(,)在椭圆上。
(I)求椭圆的离心率。
(II)设A为椭圆的右顶点,O为坐标原点,若Q在椭圆上且满足|AQ|=|AO|求直线的斜率的值。
29、【2012高考新课标文20】
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(I)若∠BFD=90°,△ABD的面积为4,求p的值及圆F的方程;
(II)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
30、【2102高考福建文21】
如图,等边三角形OAB的边长为,且其三个顶点均在抛物线E:x2=2py(p>0)上。
(1) 求抛物线E的方程;
(2) 设动直线l与抛物线E相切于点P,与直线y=-1相较于点Q。证明以PQ为直径的圆恒过y轴上某定点。
31、【2012高考山东文21】
如图,椭圆的离心率为,直线和所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线与椭圆M有两个不同的交点与矩形ABCD有两个不同的交点.求的最大值及取得最大值时m的值.
32、【2102高考北京文19】
已知椭圆C:+=1(a>b>0)的一个顶点为A (2,0),离心率为, 直线y=k(x-1)与椭圆C交与不同的两点M,N
(Ⅰ)求椭圆C的方程
(Ⅱ)当△AMN的面积为时,求k的值
33、【2012高考广东文20】
在平面直角坐标系中,已知椭圆:()的左焦点为,且点在上.
(1)求椭圆的方程;
(2)设直线同时与椭圆和抛物线:相切,求直线的方程.
34、【2012高考安徽文20】
如图,分别是椭圆:+=1()的左、右焦点,是椭圆的顶点,是直线与椭圆的另一个交点,=60°.
(Ⅰ)求椭圆的离心率;
(Ⅱ)已知△的面积为40,求a, b 的值.
35、【2012高考江苏19】如图,在平面直角坐标系中,椭圆的左、右焦点分别为,.已知和都在椭圆上,其中为椭圆的离心率.
(1)求椭圆的方程;
(2)设是椭圆上位于轴上方的两点,且直线与直线平行,与交于点P.
(i)若,求直线的斜率;
(ii)求证:是定值.
36、【2012高考陕西文20】
已知椭圆,椭圆以的长轴为短轴,且与有相同的离心率。
(1)求椭圆的方程;
(2)设O为坐标原点,点A,B分别在椭圆和上,,求直线的方程。
37、【2012高考浙江文22】如图,在直角坐标系xOy中,点P(1,)到抛物线C:=2px(P>0)的准线的距离为。点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分。
(1)求p,t的值。
(2)求△ABP面积的最大值。
以下是答案
一、选择题
1、 B
2、 C【解析】根据焦点坐标知,由双曲线的简单几何性质知,所以,因此.故选C.
3、 C
4、 B
5、 B
6、 B
7、 B
8、 C
9、 C
10、 D
11、 C
12、 A
二、填空题
13、 1,2
14、 ,
15、
16、 2。
17、 .
18、
19、
三、解答题
20、
21、 (Ⅰ)+=1(Ⅱ)
22、
23、
24、
【解析】本题主要考查直线、圆、椭圆的方程,椭圆的几何性质,轨迹方程的求法,考查函数方程思想、转化思想、数形结合思想、运算求解能力和推理论证能力,难度较大。
25、
26、
【解析】本题考查椭圆的标准方程,直线与圆锥曲线的位置关系;考查分类讨论的数学思想以及运算求解的能力.本题是一个椭圆模型,求解标准方程时注意对焦点的位置分类讨论,不要漏解;对于探讨性问题一直是高考考查的热点,一般先假设结论成立,再逆推所需要求解的条件,对运算求解能力和逻辑推理能力有较高的要求.
27、 【解析】(Ⅰ)由,得.故圆C的圆心为点
从而可设椭圆E的方程为其焦距为,由题设知
故椭圆E的方程为:
(Ⅱ)设点的坐标为,的斜分率分别为则的方程分别为且由与圆相切,得
,
即
同理可得 .
从而是方程的两个实根,于是
①
且
由得解得或
由得由得它们满足①式,故点P的坐标为
,或,或,或.
【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问根据条件设出椭圆方程,求出即得椭圆E的方程,第二问设出点P坐标,利用过P点的两条直线斜率之积为,得出关于点P坐标的一个方程,利用点P在椭圆上得出另一方程,联立两个方程得点P坐标.
28、
29、
30、
31、 (I)……①
矩形ABCD面积为8,即……②
由①②解得:,
∴椭圆M的标准方程是.
(II),
设,则,
由得.
.
当过点时,,当过点时,.
①当时,有,
,
其中,由此知当,即时,取得最大值.
②由对称性,可知若,则当时,取得最大值.
③当时,,,
由此知,当时,取得最大值.
综上可知,当和0时,取得最大值.
32、
33、 【解析】(1)因为椭圆的左焦点为,所以,
点代入椭圆,得,即,
所以,
所以椭圆的方程为.
(2)直线的斜率显然存在,设直线的方程为,
,消去并整理得,
因为直线与椭圆相切,所以,
整理得 ①
,消去并整理得。
因为直线与抛物线相切,所以,
整理得 ②
综合①②,解得或。
所以直线的方程为或。
34、
35、解:(1)由题设知,,由点在椭圆上,得
,∴。
由点在椭圆上,得
∴椭圆的方程为。
(2)由(1)得,,又∵∥,
∴设、的方程分别为,。
∴。
∴。①
同理,。②
(i)由①②得,。解得=2。
∵注意到,∴。
∴直线的斜率为。
(ii)证明:∵∥,∴,即。
∴。
由点在椭圆上知,,∴。
同理。。
∴
由①②得,,,
∴。
∴是定值。
【考点】椭圆的性质,直线方程,两点间的距离公式。
【解析】(1)根据椭圆的性质和已知和都在椭圆上列式求解。
(2)根据已知条件,用待定系数法求解。
36、
37、 (1)由题意得,得.
(2)设,线段AB的中点坐标为
由题意得,设直线AB的斜率为k(k).
由,得,得
所以直线的方程为,即.
由,整理得,
所以,,.从而得
,
设点P到直线AB的距离为d,则
,设ABP的面积为S,则.
由,得.
令,,则.
设,,则.
由,得,所以,故ABP的面积的最大值为.