贵州省毕节市梁才学校2019-2020学年高二上学期期中考试数学（理）试卷

贵州省毕节市梁才学校2019-2020学年高二上学期期中考试数学（理）试卷

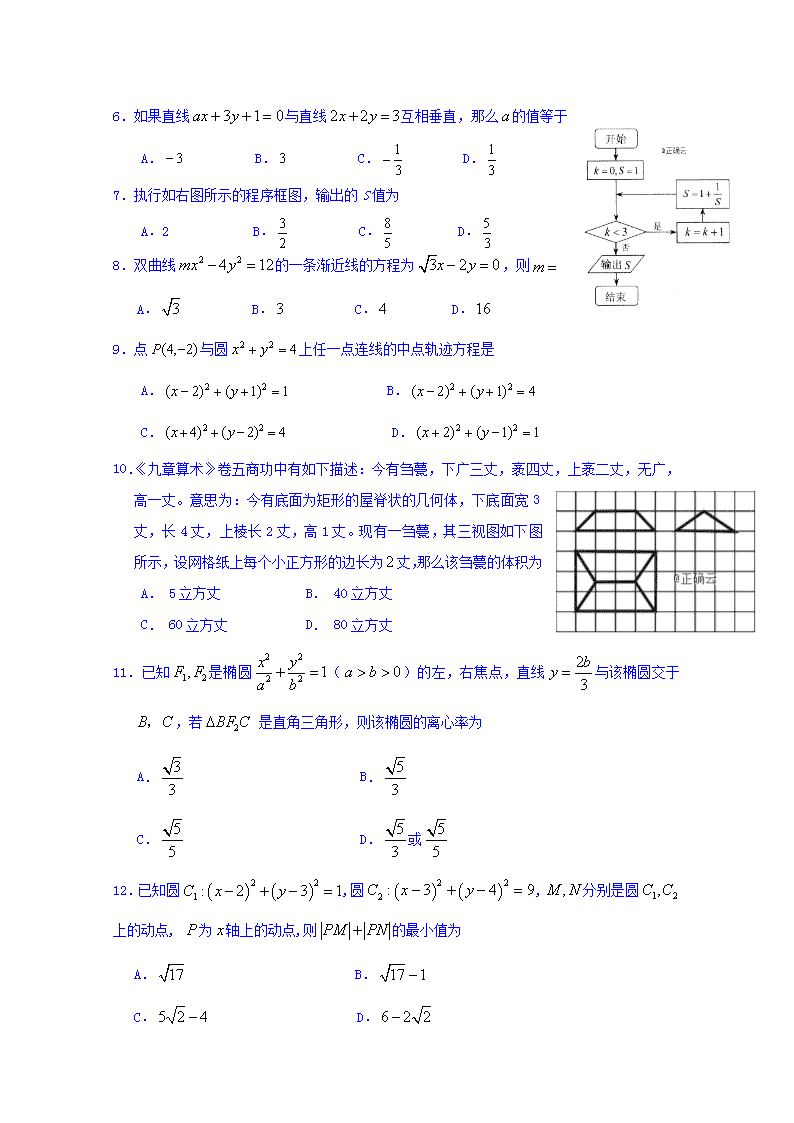
贵州省毕节梁才学校高2018级2019年秋期半期考试 数学试题（理科）‎ 考试时间：120分钟 分值：150分 ‎ 注意事项：‎ ‎1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.答题前，考生务必将自己的姓名、考生号填写在答题卡上。‎ ‎2.回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号,写在试卷上无效.‎ ‎3.回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效.‎ ‎4.考试结束，将本试卷和答题卡一并交回.‎ 第Ⅰ卷 一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．直线的倾斜角是 ‎ A．45°　　　　 　B．60° C．120° D． 135°‎ ‎2．已知圆的方程为，那么圆心坐标为 A．（1，3） B．（1，） C．（，3） D．（，）‎ ‎3．‎ A． B． C． D．‎ ‎4．如果直线平行于平面，则 ‎ A．平面内有且只有一直线与平行 B．平面内有无数条直线与平行 ‎ C．平面内不存在与垂直的直线 D．平面内有且仅有一条与垂直的直线 ‎5．设, 则是的 A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分也非必要条件 ‎6．如果直线与直线互相垂直，那么的值等于 ‎ ‎　 A． B． C． D．‎ ‎7．执行如右图所示的程序框图，输出的S值为 ‎ ‎ A．2 B． C． D．‎ ‎8．双曲线的一条渐近线的方程为，则 A． B． C． D．‎ ‎9．点与圆上任一点连线的中点轨迹方程是　 ‎ ‎ A．　　　 B．‎ ‎ C．　　　 D．‎ ‎10．《九章算术》卷五商功中有如下描述：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈。意思为：今有底面为矩形的屋脊状的几何体，下底面宽3丈，长4丈，上棱长2丈，高1丈。现有一刍甍，其三视图如下图所示，设网格纸上每个小正方形的边长为丈，那么该刍甍的体积为 A． 5立方丈 B． 40立方丈 ‎ C． 60立方丈 D． 80立方丈 ‎ ‎11．已知是椭圆（）的左，右焦点，直线与该椭圆交于，若 是直角三角形，则该椭圆的离心率为 A． B． ‎ C． D．或 ‎12．已知圆,圆,分别是圆上的动点, 为轴上的动点,则的最小值为 ‎ ‎ A． B． ‎ C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．已知球O的半径为1，则球O的外切正方体的表面积为_ ______ ．‎ ‎14．经过的直线方程是 ．‎ ‎15．若中心在原点的椭圆与双曲线有公共的焦点，且它们的离心率互为倒数，则该椭圆的标准方程为 ．‎ ‎16．如图，点P在长方体ABCD－A1B1C1D1的面对角线BC1（线段BC1）上运动，给出下列四个说法：‎ ‎① 直线AD与直线B1P为异面直线；‎ ‎　　② 恒有A1P∥面ACD1；‎ ‎　　③ 三棱锥A－D1PC的体积为定值；‎ ‎　　④ 当长方体各棱长都相等时，面PDB1⊥面ACD1．‎ 其中所有正确说法的序号是 ．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． ‎ ‎17．（本题满分10分）‎ 已知直线. ‎ ‎（Ⅰ）求直线关于轴对称的直线的方程；‎ ‎（Ⅱ）当直线，且它们的距离等于时，求直线的方程. ‎ ‎18．（本题满分12分）‎ 已知，命题，命题．‎ ‎（Ⅰ）若命题为真命题，求实数a的取值范围；‎ ‎（Ⅱ）若命题“”为假命题，求实数a的取值范围．‎ ‎19．（本题满分12分）‎ 在平面直角坐标系中xOy中，直线x+y+4=0与圆C相切，圆心C的坐标为（1，-2）．‎ ‎（Ⅰ）求圆C的方程；‎ ‎（Ⅱ）设直线y=kx+1圆C没有公共点，求k的取值范围．‎ ‎20．（本题满分12分）‎ 已知椭圆C：和点M（2，1）‎ ‎（Ⅰ）求椭圆C的焦点坐标和离心率；‎ ‎（Ⅱ）设直线椭圆交于两点，当点M是线段的中点时，求直线的方程.‎ ‎21．（本题满分12分）‎ 已知如图，矩形ABCD所在平面垂直于直角梯形ABPE所在平面，且相交于直线， .‎ Ⅰ设点M为棱PD中点，求证：；‎ Ⅱ的余弦值.‎ ‎22．（本题满分12分）‎ 已知点F为抛物线的焦点，点P是准线l上的动点，直线PF交抛物线于两点，若点P的纵坐标为，点D为准线l与x轴的交点．‎ Ⅰ求直线PF的方程 Ⅱ求的面积S范围；‎ Ⅲ设，求证为定值． ‎