- 2021-06-11 发布 |
- 37.5 KB |
- 7页


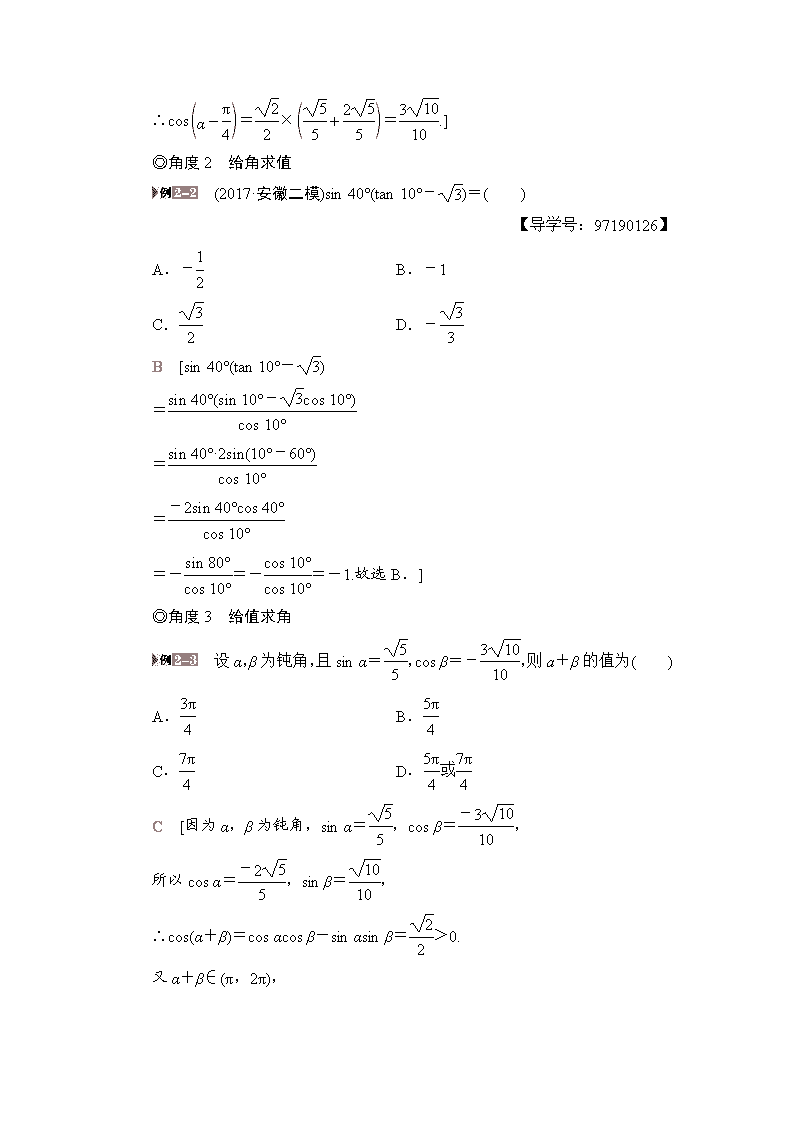
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习人教A版理第3章第6节 简单的三角恒等变换教案
第六节 简单的三角恒等变换 (对应学生用书第60页) 三角函数式的化简 (1)化简:=________. (2)化简:. (1)2cos α [原式==2cos α.] (2)[解] 原式= == =cos 2x. [规律方法] 1.三角函数式的化简要遵循“三看”原则 一看“角”,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式. 二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,最常见的是“切化弦”. 三看“结构特征”,分析结构特征,找到变形的方向. 2.三角函数式化简的方法 弦切互化,异名化同名,异角化同角,化异次为同次. [跟踪训练] 化简: (0<θ<π). [解] 原式 = =cos · =. ∵0<θ<π,∴0<<,∴cos>0, ∴原式=-cos θ. 三角式的求值 ◎角度1 给值求值 (2017·全国卷Ⅰ)已知α∈,tan α=2,则cos=________. [cos=cos αcos +sin αsin =(cos α+sin α). 又由α∈,tan α=2,知sin α=,cos α=, ∴cos=×=.] ◎角度2 给角求值 (2017·安徽二模)sin 40°(tan 10°-)=( ) 【导学号:97190126】 A.- B.-1 C. D.- B [sin 40°(tan 10°-) = = = =-=-=-1.故选B.] ◎角度3 给值求角 设α,β为钝角,且sin α=,cos β=-,则a+β的值为( ) A. B. C. D.或 C [因为α,β为钝角,sin α=,cos β=, 所以cos α=,sin β=, ∴cos(α+β)=cos αcos β-sin αsin β=>0. 又α+β∈(π,2π), ∴α+β∈,∴α+β=.] [规律方法] 三角函数求值的类型与求解方法 (1)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系. (2)“给角求值”:一般所给出的角都是非特殊角,应仔细观察非特殊角与特殊角之间的关系,结合公式将非特殊角的三角函数转化为特殊角的三角函数求解. (3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,最后确定角. [跟踪训练] (1)(2016·全国卷Ⅱ)若cos=,则sin 2α=( ) A. B. C.- D.- (2)(2017·湖北新联考四模)=( ) A. B. C. D.1 (3)已知tan α,tan β是方程x+3x+4=0的两根,且α,β∈,则α+β=( ) A. B.或- C.-或 D.- (1)D (2)A (3)D [(1)因为cos=, 所以sin 2α=cos=cos 2 =2cos-1=2×-1=-. (2)= ===.故选A. (3)由题意得tan α+tan β=-3<0,tan αtan β=4>0,所以tan(α+β)==,且tan α<0,tan β<0,又由α,β∈得α,β∈,所以α+β∈(-π,0),所以α+β=-.] 三角恒等变换的简单应用 已知函数f(x)=sinx-sin,x∈R. (1)求f(x)的最小正周期; (2)求f(x)在区间上的最大值和最小值. 【导学号:97190127】 [解] (1)由已知,有 f(x)=- =-cos 2x =sin 2x-cos 2x=sin. 所以f(x)的最小正周期T==π. (2)因为f(x)在区间上是减函数, 在区间上是增函数, 且f=-,f=-,f=, 所以f(x)在区间上的最大值为,最小值为-. [规律方法] 三角恒等变换应用问题的求解方法 (1)进行三角恒等变换要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形使用. (2)把形如y=asin x+bcos x的函数化为y=·sin(x+φ)的形式,可进一步研究函数的周期、单调性、最值与对称性. [跟踪训练] (1)(2016·山东高考)函数f(x)=(sin x+cos x)(cos x-sin x)的最小正周期是( ) A. B.π C. D.2π (2)函数f(x)=sin(x+φ)-2sin φcos x的最大值为________. (1)B (2)1 [(1)法一:∵f(x)=(sin x+cos x)(cos x-sin x) =4 =4sincos =2sin, ∴T==π. 法二:∵f(x)=(sin x+cos x)(cos x-sin x) =3sin xcos x+cosx-sinx-sin xcos x =sin 2x+cos 2x =2sin, ∴T==π. 故选B. (2)f(x)=sin(x+φ)-2sin φcos x =sin xcos φ+cos xsin φ-2sin φcos x =sin xcos φ-cos xsin φ=sin(x-φ). ∴f(x)max=1.]查看更多