【数学】2020届一轮复习人教A版 绝对值不等式 学案
第一节 绝对值不等式
1.绝对值三角不等式
定理1:如果a,b是实数,那么|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立。
定理2:如果a,b,c是实数,那么|a-b|≤|a-c|+|c-b|,当且仅当(a-c)(c-b)≥0时,等号成立。
2.绝对值不等式的解法
(1)含绝对值的不等式|x|<a与|x|>a的解集:
不等式
a>0
a=0
a<0
|x|<a
{x|-a<x<a}
∅
∅
|x|>a
{x|x>a或x<-a}
{x|x∈R且x≠0}
R
(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法:
①|ax+b|≤c⇔-c≤ax+b≤c;
②|ax+b|≥c⇔ax+b≥c或ax+b≤-c。
1.|a+b|与|a|-|b|,|a-b|与|a|-|b|,|a|+|b|之间的关系:
(1)|a+b|≥|a|-|b|,当且仅当ab≤0且|a|≥|b|时,等号成立。
(2)|a|-|b|≤|a-b|≤|a|+|b|,当且仅当|a|≥|b|且ab≥0时,左边等号成立,当且仅当ab≤0时,右边等号成立。
2.解绝对值不等式的两个要点:
(1)解绝对值不等式的关键是去掉绝对值符号。
(2)解含绝对值的不等式的基本思路可概括为十二字口诀“找零点,分区间,逐个解,并起来”。
一、走进教材
1.(选修4-5P20T7改编)不等式3≤|5-2x|<9的解集为( )
A.[-2,1)∪[4,7) B.(-2,1]∪(4,7]
C.(-2,-1)∪[4,7) D.(-2,1]∪[4,7)
解析 由题意得即
解得不等式的解集为(-2,1]∪[4,7)。故选D。
答案 D
2.(选修4-5P20T8改编)不等式|x-1|-|x-5|<2的解集是________。
解析 ①当x≤1时,原不等式可化为1-x-(5-x)<2,所以-4<2,不等式恒成立,所以x≤1;
②当1
1-x的解集。
解 (1)因为f(x)=|x+4|,
所以y=f(2x+a)+f(2x-a)=|2x+a+4|+|2x-a+4|≥|2x+a+4-(2x-a+4)|=|2a|,
又y=f(2x+a)+f(2x-a)的最小值为4,
所以|2a|=4,所以a=±2。
(2)f(x)=|x+4|=
所以不等式f(x)>1-x等价于
解得x>-2或x<-10,
故不等式f(x)>1-x的解集为{x|x>-2或x<-10}。
含绝对值不等式常见的三种解法
1.零点分段讨论法。
2.利用绝对值的几何意义。
3.数形结合法。
【变式训练】 (2018·河南新乡二模)已知函数f(x)=|x-4|+|x-1|-3。
(1)求不等式f(x)≤2的解集;
(2)若直线y=kx-2与函数f(x)的图象有公共点,求k的取值范围。
解 (1)由f(x)≤2,得或或
解得0≤x≤5,
故不等式f(x)≤2的解集为{x|0≤x≤5}。
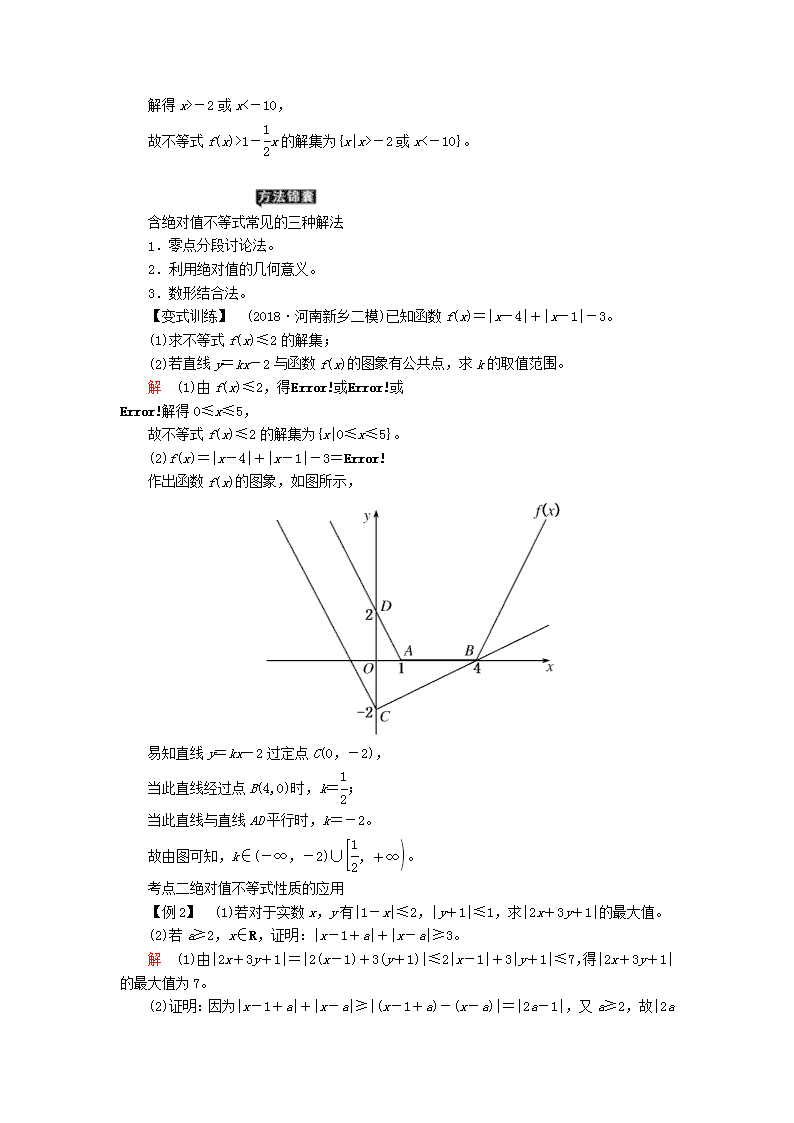
(2)f(x)=|x-4|+|x-1|-3=
作出函数f(x)的图象,如图所示,
易知直线y=kx-2过定点C(0,-2),
当此直线经过点B(4,0)时,k=;
当此直线与直线AD平行时,k=-2。
故由图可知,k∈(-∞,-2)∪。
考点二绝对值不等式性质的应用
【例2】 (1)若对于实数x,y有|1-x|≤2,|y+1|≤1,求|2x+3y+1|的最大值。
(2)若a≥2,x∈R,证明:|x-1+a|+|x-a|≥3。
解 (1)由|2x+3y+1|=|2(x-1)+3(y+1)|≤2|x-1|+3|y+1|≤7,得|2x+3y+1|的最大值为7。
(2)证明:因为|x-1+a|+|x-a|≥|(x-1+a)-(x-a)|=|2a-1|,又a≥2,故|2a
-1|≥3,即|x-1+a|+|x-a|≥3成立。
绝对值不等式性质的应用
利用不等式|a+b|≤|a|+|b|(a,b∈R)和|a-b|≤|a-c|+|c-b|(a,b∈R),通过确定适当的a,b,利用整体思想或使函数、不等式中不含变量,可以①求最值;②证明不等式。
【变式训练】 (1)设a>0,|x-1|<,|y-2|<,求证:|2x+y-4|a有解⇔f(x)max>a。
2.f(x)>a恒成立⇔f(x)min>a。
3.f(x)>a恰在(c,b)上成立⇔c,b是方程f(x)=a的解。
【变式训练】 已知f(x)=|ax-1|,若实数a>0,不等式f(x)≤3的解集是{x|-1≤x≤2}。
(1)求a的值;
(2)若<|k|存在实数解,求实数k的取值范围。
解 (1)由|ax-1|≤3,得-3≤ax-1≤3,即-2≤ax≤4。
因为a>0,所以-≤x≤,
因为不等式f(x)≤3的解集是{x|-1≤x≤2},
所以解得a=2。
(2)因为=≥=,
所以要使<|k|存在实数解,只需|k|>,解得k>或k<-,
所以实数k的取值范围是∪。
1.(配合例1、例2使用)设函数f(x)=|2x-3|。
(1)求不等式f(x)>5-|x+2|的解集;
(2)若g(x)=f(x+m)+f(x-m)的最小值为4,求实数m的值。
解 (1)因为f(x)>5-|x+2|可化为|2x-3|+|x+2|>5,
所以当x≥时,原不等式化为(2x-3)+(x+2)>5,解得x>2,所以x>2;
当-25,解得x<0,所以-25,解得x<-,所以x≤-2。
综上,不等式f(x)>5-|x+2|的解集为(-∞,0)∪(2,+∞)。
(2)因为f(x)=|2x-3|,
所以g(x)=f(x+m)+f(x-m)=|2x+2m-3|+|2x-2m-3|≥|(2x+2m-3)-(2x-2m-3)|=|4m|。
所以依题意有4|m|=4,解得m=±1。
2.(配合例3使用)已知函数f(x)=|2x-a|+|2x+3|,g(x)=|x-1|+2。
(1)解不等式|g(x)|<5;
(2)若对任意x1∈R,都存在x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围。
解 (1)由||x-1|+2|<5,得-5<|x-1|+2<5,
所以-7<|x-1|<3,即|x-1|<3,解得-2
查看更多