【数学】江西省赣州市赣县第三中学2020-2021学年高二上学期8月入学考试试卷（奥赛班）

【数学】江西省赣州市赣县第三中学2020-2021学年高二上学期8月入学考试试卷（奥赛班）

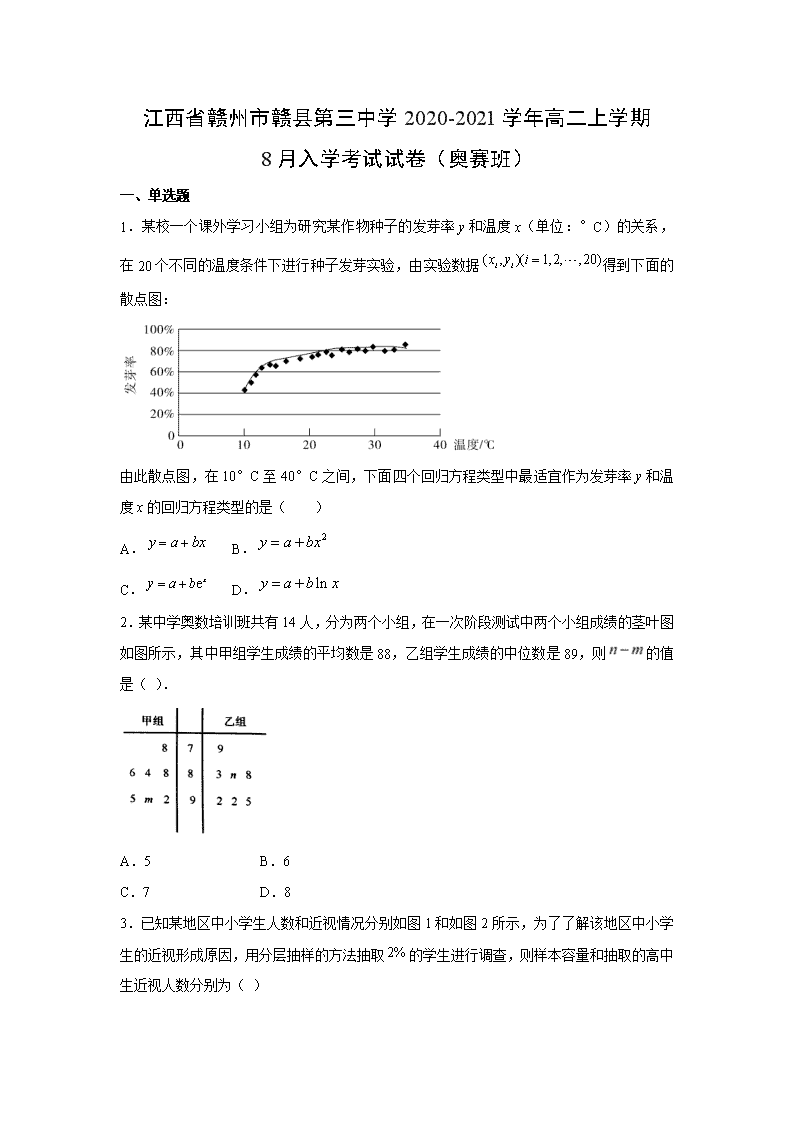
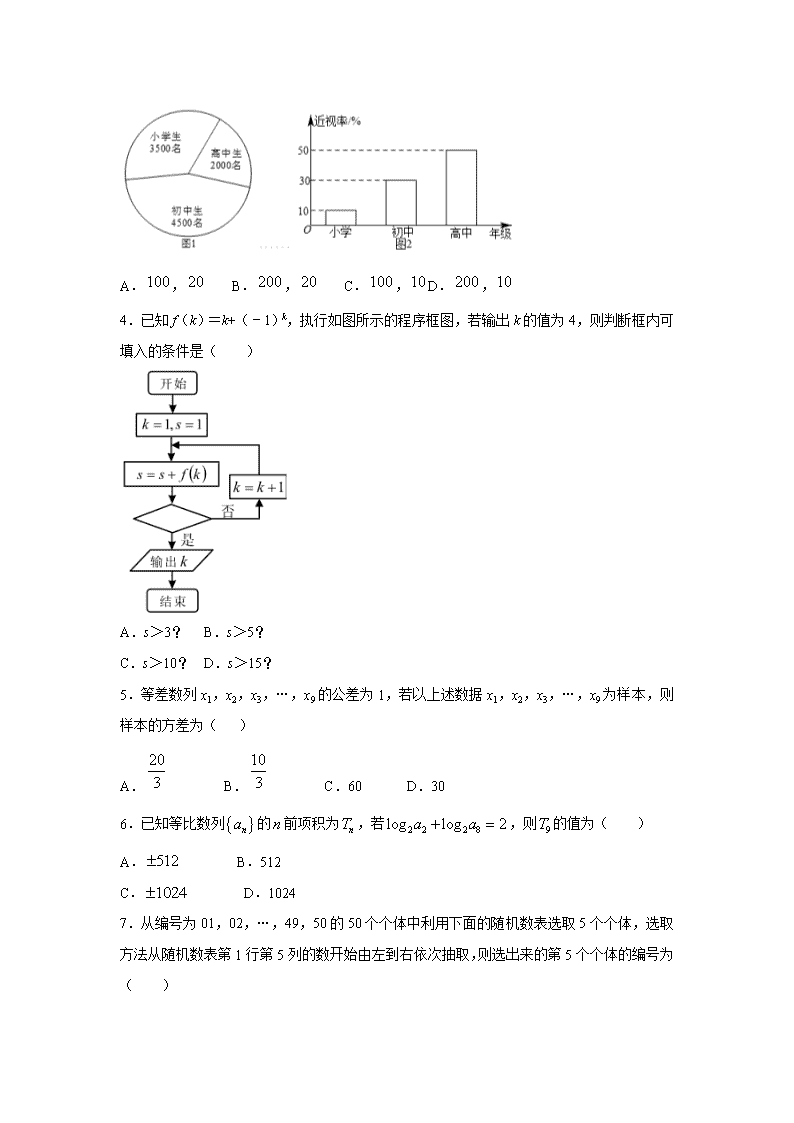
www.ks5u.com 江西省赣州市赣县第三中学2020-2021学年高二上学期 ‎8月入学考试试卷（奥赛班）‎ 一、单选题 ‎1．某校一个课外学习小组为研究某作物种子的发芽率y和温度x（单位：°C）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据得到下面的散点图：‎ 由此散点图，在10°C至40°C之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是（ ）‎ A． B．‎ C． D．‎ ‎2．某中学奥数培训班共有14人，分为两个小组，在一次阶段测试中两个小组成绩的茎叶图如图所示，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则的值是（ ）．‎ A．5 B．6 ‎ C．7 D．8‎ ‎3．已知某地区中小学生人数和近视情况分别如图1和如图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取的学生进行调查，则样本容量和抽取的高中生近视人数分别为（ ）‎ A．， B．， C．， D．，‎ ‎4．已知f（k）＝k+（﹣1）k，执行如图所示的程序框图，若输出k的值为4，则判断框内可填入的条件是（ ）‎ A．s＞3？ B．s＞5？ ‎ C．s＞10？ D．s＞15？‎ ‎5．等差数列x1，x2，x3，…，x9的公差为1，若以上述数据x1，x2，x3，…，x9为样本，则样本的方差为（ ）‎ A． B． C．60 D．30‎ ‎6．已知等比数列的前项积为，若，则的值为（ ）‎ A． B．512 ‎ C． D．1024‎ ‎7．从编号为01，02，…，49，50的50个个体中利用下面的随机数表选取5个个体，选取方法从随机数表第1行第5列的数开始由左到右依次抽取，则选出来的第5个个体的编号为（ ）‎ ‎7816‎ ‎6572‎ ‎0812‎ ‎1463‎ ‎0782‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A．14 B．07 C．32 D．43‎ ‎8．某中学教务处采用系统抽样方法，从学校高一年级全体名学生中抽名学生做学习状况问卷调查.现将名学生从到进行编号．在第一组中随机抽取一个号，如果抽到的是号，则第组中应取的号码是（ ）‎ A． B． C． D．‎ ‎9．执行如图所示的程序框图，输出的结果为　　‎ A． B． C． D．‎ ‎10．已知直线恒过定点A，点A也在直线上，其中均为正数，则的最小值为（ ）‎ A．2 B．4 C．6 D．8‎ ‎11．，，分别为内角，，的对边.已知，，则的面积的最大值为（ ）‎ A．1 B． C． D．‎ ‎12．在数列中，，，且，为数列的前项和，则（ ）‎ A． B． C． D．‎ 二、填空题 ‎13．过点且在两坐标轴上的截距相等的直线方程为____________.‎ ‎14．将一颗骰子先后投掷两次分别得到点数，则直线与圆有公共点的概率为________.‎ ‎15．如图，在边长为2的正六边形内随机地撒一把豆子，落在正六边形内的豆子粒数为626，落在阴影区域内的豆子粒数为313，据此估计阴影的面积为_______.‎ ‎16．如图，嵩山上原有一条笔直的山路，现在又新架设了一条索道，小李在山脚处看索道，发现张角；从处攀登400米到达处，回头看索道，发现张角；从处再攀登800米方到达处，则索道的长为________米． ‎ 三、解答题 ‎17．某学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月11日至3月15日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料：‎ 日期 ‎3月11日 ‎3月12日 ‎3月13日 ‎3月14日 ‎3月15日 昼夜温差（）‎ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数（颗）‎ ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ ‎（1）请根据3月12日至3月14日的三组数据，求出关于的线性回归方程 ；‎ ‎（2）若由线性回归方程得到的估计数据与所需要检验的数据误差均不超过2颗，则认为得到的线性回归方程是可靠的，试用3月11日与3月15日的两组数据检验，问（1）中所得的线性回归方程是否可靠？（参考公式：，）‎ ‎18．已知点，圆．‎ ‎（1）求过点M的圆的切线方程；‎ ‎（2）若直线与圆相交于A，B两点，且弦AB的长为，求的值．‎ ‎19．某城市户居民的月平均用电量（单位：度），以，，，，，，‎ 分组的频率分布直方图如图．‎ ‎（1）求直方图中的值；‎ ‎（2）求月平均用电量的众数和中位数；‎ ‎（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？‎ ‎20．已知数列的各项均为正数，观察程序框图，若时，分别有和.‎ ‎（Ⅰ）试求数列的通项公式；‎ ‎（Ⅱ）令，求数列的前项和.‎ ‎21．在锐角中，分别为所对的边，已知.‎ ‎（1）求的值；‎ ‎（2）为中点，，，求的面积.‎ ‎22．党的十九大报告指出，要以创新理念提升农业发展新动力，引领经济发展走向更高形态.为进一步推进农村经济结构调整，某村举办水果观光采摘节，并推出配套乡村游项目现统计了4月份200名游客购买水果的情况，得到如图所示的频率分布直方图：‎ ‎（1）若将购买金额不低于80元的游客称为“水果达人”，现用分层抽样的方法从样本的“水果达人”中抽取5人，求这5人中消费金额不低于100元的人数；‎ ‎（2）从（1）中的5人中抽取2人作为幸运客户免费参加山村旅游项目，请列出所有的基本事件，并求2人中至少有1人购买金额不低于100元的概率；‎ ‎（3）为吸引顾客，该村特推出两种促销方案，‎ 方案一：每满80元可立减8元；‎ 方案二：金额超过50元但又不超过80元的部分打9折，金额超过80元但又不超过100元的部分打8折，金额超过100元的部分打7折.‎ 若水果的价格为11元/千克，某游客要购买10千克，应该选择哪种方案更优惠.‎ ‎【参考答案】‎ ‎1.D2．B4．C5．A6．A7．D8．C9．C10．D11．D12．C ‎13．x+y=3或y=2x 14． 15． 16．400‎ ‎17．解:（1）由表中数据，求得，‎ ‎，，‎ ‎，‎ ‎，；‎ 由公式求得，‎ ‎，‎ 所以关于的线性回归方程为；‎ ‎（2）当时，，；‎ 同样，当时，，；‎ 所以，该研究所得到的线性回归方程是可靠的．‎ ‎18．解：（1）由题意知圆心的坐标为,半径,‎ 当过点M的直线的斜率不存在时,方程为．‎ 由圆心到直线的距离知,此时,直线与圆相切．‎ 当过点M的直线的斜率存在时,设方程为,‎ 即．由题意知,‎ 解得,∴方程为．‎ 故过点M的圆的切线方程为或．‎ ‎（2）∵圆心到直线的距离为,‎ ‎∴,解得．‎ ‎19．解：(1)由直方图的性质可得 ‎(0.002＋0.0095＋0.011＋0.0125＋x＋0.005＋0.0025)×20＝1得：‎ x＝0.0075，所以直方图中x的值是0.0075. ------------- 3分 ‎(2)月平均用电量的众数是＝230. ------------- 5分 因为(0.002＋0.0095＋0.011)×20＝0.45<0.5，所以月平均用电量的中位数在[220,240)内，‎ 设中位数为a，‎ 由(0.002＋0.0095＋0.011)×20＋0.0125×(a－220)＝0.5‎ 得：a＝224，所以月平均用电量的中位数是224. ------------ 8分 ‎(3)月平均用电量为[220,240)的用户有0.0125×20×100＝25户，‎ 月平均用电量为[240,260)的用户有0.0075×20×100＝15户，‎ 月平均用电量为[260,280)的用户有0. 005×20×100＝10户，‎ 月平均用电量为[280,300]的用户有0.0025×20×100＝5户， -------------10分 抽取比例＝＝，‎ 所以月平均用电量在[220,240)的用户中应抽取25×＝5户．-- 12分 ‎20．解：（Ⅰ）由条件知：数列为各项均为正数且公差为的等差数列，‎ 时，，‎ 时，， ‎ 即：，，解得：， ‎ 所以：.‎ ‎（Ⅱ）， ‎ 所以：，即.‎ ‎21．（1）由正弦定理得：，‎ 即，‎ ‎，，.‎ ‎（2）为中点，，‎ 两边平方得：，‎ ‎，解得：，‎ 由（1）知：，又，，‎ ‎.‎ ‎22．解：（1）由图可知，‎ 消费金额在“水果达人”的人数为：人，‎ 消费金额在“水果达人”的人数为：人，‎ 分层抽样的方法从样本的“水果达人”中抽取5人，这5人中消费金额不低于100元的人数为：人；‎ ‎（2）由（1）得，‎ 消费金额在的3个“水果达人”记为，，，‎ 消费金额在的2个“水果达人”记为，，‎ 所有基本事件有：，，，，，，，，，共种，‎ ‎2人中至少有1人购买金额不低于100元的有种，所求概率为.‎ ‎（3）依题可知该游客要购买110元的水果，‎ 若选择方案一，则需支付元，‎ 若选择方案二，则需支付元，‎ 所以应该选择方案二更优惠.‎