- 2021-06-11 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
安徽省蚌埠市2020届高三下学期第三次教学质量检查考试 数学(理)
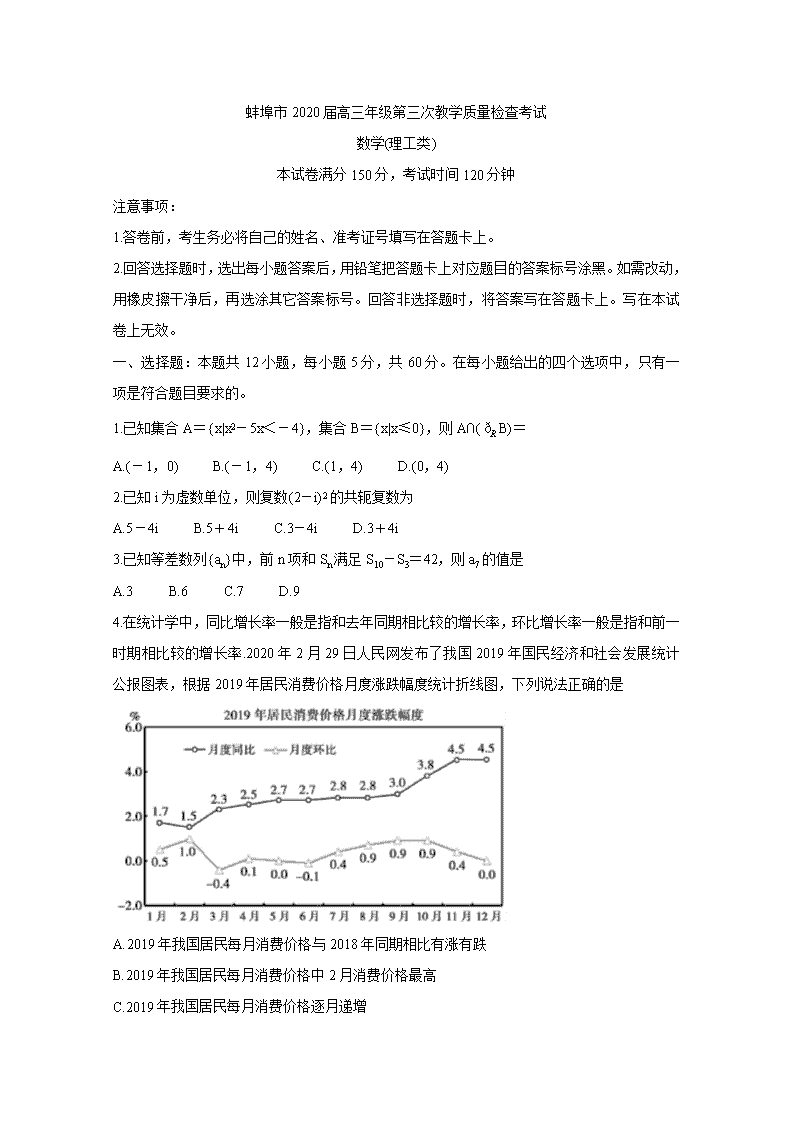
蚌埠市2020届高三年级第三次教学质量检查考试 数学(理工类) 本试卷满分150分,考试时间120分钟 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。 一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.已知集合A={x|x2-5x<-4},集合B={x|x≤0},则A∩(B)= A.(-1,0) B.(-1,4) C.(1,4) D.(0,4) 2.已知i为虚数单位,则复数(2-i)2的共轭复数为 A.5-4i B.5+4i C.3-4i D.3+4i 3.已知等差数列{an}中,前n项和Sn满足S10-S3=42,则a7的值是 A.3 B.6 C.7 D.9 4.在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是 A.2019年我国居民每月消费价格与2018年同期相比有涨有跌 B.2019年我国居民每月消费价格中2月消费价格最高 C.2019年我国居民每月消费价格逐月递增 D.2019年我国居民每月消费价格3月份较2月份有所下降 5.已知双曲线C:离心率为3,则双曲线C的渐近线方程为 A.y=±x B.y=±x C.y=±2x D.y=±x 6.已知向量a,b的夹角为,a=(1,2),a·(a+2b)=0,则|b|等于 A. B.2 C. D. 7.劳动教育是中国特色社会主义教育制度的重要内容,某高中计划组织学生参与各项职业体验,让学生在劳动课程中掌握一定劳动技能,理解劳动创造价值,培养劳动自立意识和主动服务他人、服务社会的情怀。学校计划下周在高一年级开设“缝纫体验课”,聘请“织补匠人”李阿姨给同学们传授织补技艺。高一年级有6个班,李阿姨每周一到周五只有下午第2节课的时间可以给同学们上课,所以必须安排有两个班合班上课,高一年级6个班“缝纫体验课”的不同上课顺序有 A.600种 B.3600种 C.1200种 D.1800种 8.函数f(x)=sin2x的图象是由函数g(x)=cos(2x-φ)(0≤φ≤π)的图象向右平移个单 位长度后得到,则下列是函数y=g(x)的图象的对称轴方程的为 A.x= B.x= C.x= D.x=0 9.已知椭圆的离心率为,左、右焦点分别为F1,F2,过左焦点F1作直线与椭圆在第一象限交点为P,若△PF1F2为等腰三角形,则直线PF1的斜率为 A. B. C. D. 10.已知函数f(x)的图象如图所示,则函数f(x)的解析式可能是 A.y=x(1-|x|) B.y=cos(x) C.y=sin(πx) D.y=|x|(1-x)(x+1) 11.开学后,某学校食堂为了减少师生就餐排队时间,特推出即点即取的米饭套餐和面食套餐两种,已知小明同学每天中午都会在食堂提供的米饭套餐和面食套餐中选择一种,米饭套餐的价格是每份15元,面食套餐的价格是每份10元,如果小明当天选择了某种套餐,她第二天会有80%的可能性换另一种类型的套餐,假如第1天小明选择了米饭套餐,第n天选择米饭套餐的概率pn,给出以下论述: ①小明同学第二天一定选择面食套餐; ②p3=0.68; ③pn=0.2pn-1+0.8(1-pn-1)(n≥2,n∈N); ④前n天小明同学午餐花费的总费用数学期望为。 其中正确的是: A.②④ B.①②③ C.③④ D.②③④ 12.已知函数f(x)=+x-ln(ax)-2(a>0),若函数f(x)在区间(0,+∞)内存在零点,则实数a的取值范围是 A.(0,1] B.[1,+∞) C.(0,e] D.[e,+∞) 二、填空题:本题共4小题,每小题5分,共20分。 13.已知命题p:x∈R,使得cos2x+sinx+1>m,若命题p是假命题,则实数m的取值范围是 。 14.已知函数f(x)=,若f(a)=2,则a= 。 15.已知的展开式中各项系数和为2,则其展开式中常数项是 。 16.如图是第七届国际数学教育大会的会徽,它的主题图案由一连串如图所示的直角三角形演化而成。设其中的第一个直角△OA1A2是等腰三角形,且A1A2=A2A3=…=AnAn+1=1,则OA2=,OA3=,…OAn=,现将△OA1A2沿OA2翻折成△OPA2,则当四面体OPA2A3体积最大时,它的侧面有 个直角三角形;当PA3=1时,四面体OPA2A3外接球的体积为 。 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。 (一)必考题:共60分。 17.(12分) 在△ABC中,角A,B,C所对的边长分别为a,b,c,它的外接圆半径为,且csinA=4sinB-acosC。 (1)求角A的大小; (2)求△ABC周长的最大值。 18.(12分) 随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一。随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世--蚂蚁花呗。这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求。为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如下图所示。 (1)由大数据可知,在18到44岁之间各年龄段使用花呗“赊购”的人数百分比y与年龄x 成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字); (2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数; (3)已知该网站中年龄段在18-26岁和27-35岁的注册用户人数相同.现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁之间的概率。 参考公式:。 19.(12分) 如图四棱柱ABCD-A1B1C1D1中,AD//BC,AB⊥AD,AD=AB=2BC,M为A1D的中点。 (1)证明:CM//平面AA1B1B; (2)若四边形A1ABB1是菱形,且面A1ABB1⊥面ABCD,∠B1BA=,求二面角A1-CM-A的余弦值。 20.(12分) 已知抛物线C:x2=2py(p>0)的焦点为F,直线y=kx+2与抛物线C交于A,B两点,若k=1,则||BF|-|AF||=4。 (1)求抛物线C的方程; (2)分别过点A,B作抛物线C的切线l1,l2,若l1,l2分别交x轴于点M,N,求四边形ABNM面积的最小值。 21.(12分) 已知函数f(x)=。 (1)分析函数f(x)的单调性; (2)证明:。 (二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。 22.[选修4-4:坐标系与参数方程](10分) 在平面直角坐标系xOy中,直线l的参数方程为,(其中t为参数,≤α<π)。在以原点O为极点,x轴的非负半轴为极轴所建立的极坐标系中,曲线C的极坐标方程为ρcos2θ=2cosθ-2ρsin2θ。设直线l与曲线C相交于A,B两点。 (1)求曲线C和直线l的直角坐标方程; (2)已知点P(0,1),求的最大值。 23.[选修4-5:不等式选讲](10分) 已知函数f(x)=|x-m|+|x|,x∈R。 (1)若不等式f(x)≥m2对x∈R恒成立,求实数m的取值范围; (2)若(1)中实数m的最大值为t,且a+b+c=t(a,b,c均为正实数)。 证明:≥9。查看更多