2021届课标版高考文科数学一轮复习教师用书：第十三章 算法初步

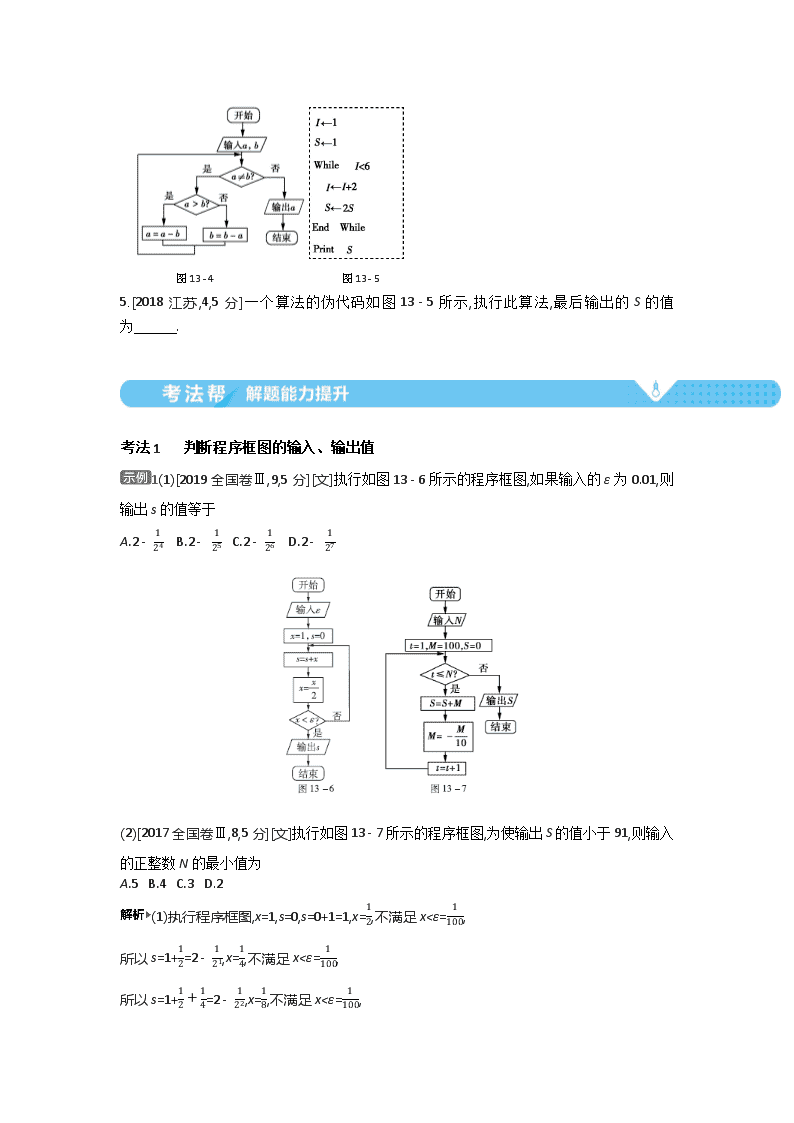
2021届课标版高考文科数学一轮复习教师用书：第十三章 算法初步

第十三章 算法初步 ‎　　　　　　　　　　　　　　　　　　　 ‎ ‎　　　　　　　　　　　　　　　　　　　　　　‎ ‎1.[2020江西南昌模拟]阅读如图13 - 1所示的程序框图,该算法的功能是(　　)‎ A.求数列{2n - 1}的前5项和 ‎ B.求数列{2n - 1}的第5项 C.求数列{2n}的前6项和 ‎ D.求数列{2n - 1}的第6项 ‎2.[2019天津,4,5分][文]阅读如图13 - 2所示的程序框图,运行相应的程序,输出S的值为(　　)‎ A.5 B.8 C.24 D.29‎ ‎3.[2018全国卷Ⅱ,8,5分][文]为计算S=1 - ‎1‎‎2‎‎+‎1‎‎3‎-‎‎1‎‎4‎+…+‎1‎‎99‎‎-‎‎1‎‎100‎,设计了如图13 - 3所示的程序框图,则在空白框中应填入(　　)‎ A.i=i+1 B.i=i+2‎ C.i=i+3 D.i=i+4‎ ‎4.[2015 新课标全国Ⅱ,8,5分][文]如图13 - 4所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=(　　)‎ A.0 B.2 C.4 D.14‎ ‎　　　　图13 - 4　　　　　　　　　　　　图13 - 5‎ ‎5.[2018江苏,4,5分]一个算法的伪代码如图13 - 5所示,执行此算法,最后输出的S的值为　　　. ‎ ‎　　　　　　　　　　　　　 　　　　　　 　　　　　　 ‎ 考法1 判断程序框图的输入、输出值 ‎1(1)[2019全国卷Ⅲ,9,5分][文]执行如图13 - 6所示的程序框图,如果输入的ε为0.01,则输出s的值等于 A.2 - ‎1‎‎2‎‎4‎ B.2 - ‎ ‎‎1‎‎2‎‎5‎ C.2 - ‎1‎‎2‎‎6‎ D.2 - ‎‎ ‎‎1‎‎2‎‎7‎ ‎(2)[2017全国卷Ⅲ,8,5分][文]执行如图13 - 7所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为 A.5 B.4 C.3 D.2‎ ‎(1)执行程序框图,x=1,s=0,s=0+1=1,x=‎1‎‎2‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎=2 - ‎1‎‎2‎‎1‎,x=‎1‎‎4‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎‎+‎‎1‎‎4‎=2 - ‎1‎‎2‎‎2‎,x=‎1‎‎8‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎‎+‎1‎‎4‎+‎‎1‎‎8‎=2 - ‎1‎‎2‎‎3‎,x=‎1‎‎16‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎‎+‎1‎‎4‎+‎1‎‎8‎+‎‎1‎‎16‎=2 - ‎1‎‎2‎‎4‎,x=‎1‎‎32‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎‎+‎1‎‎4‎+‎1‎‎8‎+‎1‎‎16‎+‎‎1‎‎32‎=2 - ‎1‎‎2‎‎5‎,x=‎1‎‎64‎,不满足x<ε=‎1‎‎100‎,‎ 所以s=1+‎1‎‎2‎‎+‎1‎‎4‎+‎‎1‎‎8‎+…+‎1‎‎64‎=2 - ‎1‎‎2‎‎6‎,x=‎1‎‎128‎,满足x<ε=‎1‎‎100‎,‎ 输出s=2 - ‎ ‎‎1‎‎2‎‎6‎.‎ ‎(2) S= 0+100=100,M= - 10,t=2,100>91;S=100 - 10=90,M=1,t=3,90<91,输出S,此时,t=3不满足t≤N,所以输入的正整数N的最小值为2.‎ ‎(1)C　(2)D ‎1.(1)[2019湖北部分重点中学高三测试]执行如图13 - 8所示的程序框图,假如输入的S,k的值分别为1,2,那么输出的S=(　　)‎ A.1+‎15‎ B.‎15‎ C.4 D.‎‎17‎ ‎　　　　 图13 - 8　　　　　 　　　　　　图13 - 9‎ ‎(2)[2019南昌三模]执行如图13 - 9所示的程序框图,若输入3个不同的实数x,输出的y值相同,则此输出结果y可能是(　　)‎ A.‎1‎‎2‎ B. - 1 C.4 D. - 2‎ 考法2 补全程序框图 ‎2[2019全国卷Ⅰ,9,5分][文]如图13 - 10是求‎1‎‎2+‎‎1‎‎2+‎‎1‎‎2‎的程序框图,图中空白框中应填入 A.A=‎1‎‎2+A 　 B.A=2+‎‎1‎A C.A=‎1‎‎1+2A 　D.A=1+‎‎1‎‎2A A=‎1‎‎2‎,k=1,1≤2成立,执行循环体;A=‎1‎‎2+‎‎1‎‎2‎,k=2,2≤2成立,执行循环体;A=‎1‎‎2+‎‎1‎‎2+‎‎1‎‎2‎,k=3,3≤2不成立,结束循环,输出A.故空白框中应填入A=‎1‎‎2+A.故选A. ‎ A ‎2.[2017全国卷Ⅰ,10,5分][文]如图13 - 11所示的程序框图是为了求出满足3n - 2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入(　　)‎ A.A>1 000和n=n+1 ‎ B.A>1 000和n=n+2‎ C.A≤1 000和n=n+1‎ D.A≤1 000和n=n+2‎ 数学文化　算法与数学文化 ‎3[2016全国卷Ⅱ,9,5分][文]中国古代有计算多项式值的秦九韶算法,如图13 - 12是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=‎ A.7　　B.12　　C.17　　D.34‎ 由程序框图知,第一次循环:x=2,n=2,a=2,s=0×2+2=2,k=1.‎ 第二次循环:a=2,s=2×2+2=6,k=2.‎ 第三次循环:a=5,s=6×2+5=17,k=3. ‎ 结束循环,输出s的值为17.‎ C ‎3.[2020四川五校联考]《九章算术》中的玉石问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石立方三寸,中有玉,并重十一斤(176两),问玉、石重各几何?”其意思是:“宝玉1立方寸的质量是7两,石料1立方寸的质量是6两,现有宝玉和石料混合在一起的一个正方体的棱长是3寸,质量是11斤(176两),问这个正方体中的宝玉和石料各多少两?”如图13 - 13所示的程序框图给出了一个求解此题的算法,运行该程序框图,则输出的x,y分别为(　　)‎ A.96,80　　B.100,76　　C.98,78　　D.94,82‎ ‎1.D　由程序框图可知,需要执行6次循环体,这6次运算中A的结果分别是1,3,7,15,31,63.故选D.‎ ‎【易错警示】　本题把数列中某项的求解与程序框图结合在一起,注重知识的交汇与综合,体现能力立意.要明确每执行一次循环体的运算结果,易混淆算法功能是求和还是求项,易将退出循环体时i的取值算错.‎ ‎2.B　执行程序框图,S=1,i=2,j=1,S=1+4=5,i=3,S=8,i=4,满足i≥4,输出的S=8.故选B.‎ ‎3.B　由程序框图的算法功能知执行框N=N+‎1‎i计算的是连续奇数的倒数和,而执行框T=T+‎1‎i+1‎计算的是连续偶数的倒数和,所以在空白执行框中应填入的命令是i=i+2,故选B.‎ ‎【名师点评】　此类题目侧重于对程序框图循环结构的考查.解题时首先要明晰算法及程序框图的相关概念,其次要重视循环起始条件、循环次数、循环终止条件,最后要通过循环规律,明确程序框图的功能.‎ ‎4.B　解法一　输入a=14,b=18,因为ab,所以a=14 - 4=10;因为a=10,b=4,a>b,所以a=10 - 4=6;因为a=6,b=4,a>b,所以a=6 - 4=2;因为a=2,b=4,a16,结束循环.此时输出的结果为S=1+‎1‎‎2‎‎+1‎‎+‎‎1‎‎3‎‎+‎‎2‎+…+‎ ‎1‎‎16‎‎+‎‎15‎‎=1+(‎2‎ - 1)+(‎3‎‎ - ‎‎2‎)+…+(‎16‎‎ - ‎‎15‎)=4,故选C.‎ ‎(2)A　由程序框图可知,输出的结果是函数y=x‎2‎‎ - 4x+3,x>0,‎x+3,x≤0‎的值,画出该函数的图象,如图D 13 - 1所示,“输入3个不同的实数x,输出的y值相同”等价于“直线y=m与函数y=x‎2‎‎ - 4x+3,x>0,‎x+3,x≤0‎的图象有3个交点”,则m∈( - 1,3),结合各选项,可知只有‎1‎‎2‎∈( - 1,3),故选A.‎ 图D 13 - 1‎ ‎2.D　因为程序框图是为了求出满足A=3n - 2n>1 000的最小偶数n,且程序框图是在“否”时输出,所以中应填入A≤1 000,排除选项A,B.又n的初始值为0,所以中应填入n=n+2.故选D.‎ ‎3.C　根据题意,运行程序框图,‎ x=90,y=86,s≠27;‎ x=92,y=84,s≠27;‎ x=94,y=82,s≠27;‎ x=96,y=80,s≠27;‎ x=98,y=78,s=27.‎ 输出x,y的值分别为98和78.故选C.‎