2018届二轮复习概率统计学案（全国通用）

2018届二轮复习概率统计学案（全国通用）

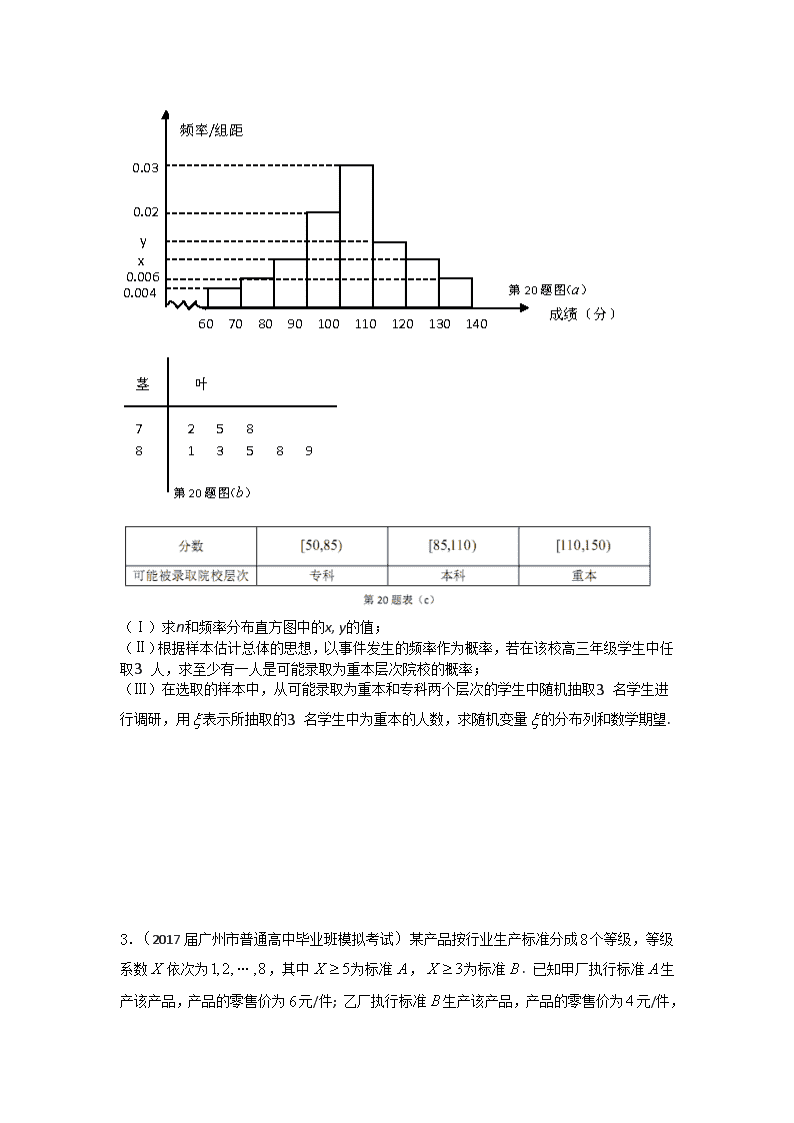
‎2017高三理科数学二轮复习导学案 专题四：概率统计 ‎1．（襄阳市优质高中2017届高三联考）近年来我国电子商务行业迎来蓬勃发展新机遇，2016年双11期间，某网络购物平台推销了A,B,C三种商品，某网购者决定抢购这三种商品，假设该名网购者都参与了A,B,C三种商品的抢购，抢购成功与否相互独立，且不重复抢购同一种商品，对A,B,C三件商品抢购成功的概率分别为，已知三件商品都被抢购成功的概率为，至少有一件商品被抢购成功的概率为.‎ ‎（1）求的值；‎ ‎（2）若购物平台准备对抢购成功的A,B,C三件商品进行优惠减免，A商品抢购成功减免2百元，B商品抢购成功减免4比百元，C商品抢购成功减免6百元.求该名网购者获得减免总金额（单位：百元）的分别列和数学期望.‎ ‎2．（东莞市2016—2017 学年度第一学期教学质量检查）某学校为了解该校高三年级学生数学科学习情况，对广一模考试数学成绩进行分析，从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140) ，按照 ‎[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图（a）所示，样本中分数在[70,90)内的所有数据的茎叶图如图（b）所示.根据上级统计划出预录分数线，有下列分数与可能被录取院校层次对照表为表（ c ）.‎ ‎（Ⅰ）求n和频率分布直方图中的x, y的值；‎ ‎（Ⅱ）根据样本估计总体的思想，以事件发生的频率作为概率，若在该校高三年级学生中任取3 人，求至少有一人是可能录取为重本层次院校的概率；‎ ‎（Ⅲ）在选取的样本中，从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研，用表示所抽取的3 名学生中为重本的人数，求随机变量的分布列和数学期望.‎ ‎3．（2017届广州市普通高中毕业班模拟考试）某产品按行业生产标准分成个等级，等级系数依次为…，其中为标准，为标准. 已知甲厂执行标准生产该产品，产品的零售价为元/件; 乙厂执行标准生产该产品，产品的零售价为 元/件，假定甲, 乙两厂的产品都符合相应的执行标准. ‎ ‎（Ⅰ）已知甲厂产品的等级系数的概率分布列如下所示：‎ 且的数学期望, 求的值;‎ ‎（Ⅱ）为分析乙厂产品的等级系数，从该厂生产的产品中随机抽取件，相应的等 级系数组成一个样本，数据如下:‎ 用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数的数学期望；‎ ‎（Ⅲ）在（Ⅰ）,（Ⅱ）的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可 购买性？说明理由.‎ 注: ①产品的“性价比”；②“性价比”大的产品更具可购买性.‎ ‎4、我市每年中考都要举行实验操作考试和体能测试，初三某班共有30名学生，下表为该班学生的这两项成绩，例如表中实验操作考试和体能测试都为优秀的学生人数为6人.由于 部分数据丢失，只知道从这班30人中随机抽取一个，实验操作成绩合格,且体能测试成 实验操作 不合格 合格 良好 优秀 体 能 测 不合格 ‎0‎ ‎0‎ ‎1‎ ‎1‎ 试 合格 ‎0‎ ‎2§xx§k.Com]‎ ‎1‎ b 良好 ‎1‎ a ‎2‎ ‎4‎ 优秀 ‎1‎ ‎2‎ ‎3‎ ‎6‎ 绩合格或合格以上的概率是.‎ ‎ （Ⅰ）试确定、的值；‎ ‎ （Ⅱ）从30人中任意抽取3人，设实 ‎ 验操作考试和体能测试成绩都是 ‎ 良好或优秀的学生人数为，求 ‎ 随机变量的分布列及数学期望 ‎ ．‎ ‎[来源:学科网ZXXK]‎ ‎5. 我国上是世界严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准（吨），用水量不超过的部分按平价收费，超过的部分按议价收费，为了了解全市民月用水量的分布情况，通过抽样，获得了100位居民某年的月用水量（单位：吨），将数据按照，，…，分成9组，制成了如图所示的频率分布直方图.‎ ‎（Ⅰ）求直方图中 的值；‎ ‎（Ⅱ）若该市政府希望使的居民每月的用水量不超过标准（吨），估计的值，并说明理由；‎ ‎（Ⅲ）已知平价收费标准为4元/吨，议价收费标准为8元/吨，当时，估计该市居民的月平均水费.（同一组中的数据用该组区间的中点值代替）‎ ‎6、某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布，下表用茎叶图列举出来抽样出的10名学生的成绩.‎ ‎(1)计算这10名学生的成绩的均值和方差；‎ ‎(2)) 给出正态分布的数据：[来源:学.科.网Z.X.X.K]‎ 由（1）估计从全市随机抽取一名学生的成绩在的概率.‎ ‎7. 某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：‎ 日期 ‎12月1日 ‎12月2日 ‎12月3日 ‎12月4日 ‎12月5日 温差（℃）‎ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数（颗）‎ ‎23[来源:Zxxk.Com]‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求回归方程，再对被选取的2组数据进行检验.‎ ‎（Ⅰ）求选取的2组数据恰好是不相邻的2天数据的概率；‎ ‎（Ⅱ）‎ 若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求关于的线性回归方程；‎ ‎（Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗，则认为得到的线性回归方程是可靠的，试问（Ⅱ）中所得的线性回归方程是否可靠？‎ ‎（注：）‎ ‎8. 为了研究家用轿车在高速公路上的车速情况，交通部门对100名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在55名男性驾驶员中，平均车速超过的有40人，不超过的有15人．在45名女性驾驶员中，平均车速超过的有20人，不超过的有25人． （Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过的人与性别有关．‎ 平均车速超过 人数 平均车速不超过 人数 合计 男性驾驶员人数 ‎      ‎ 女性驾驶员人数 ‎      ‎ 合计 ‎      ‎ ‎（Ⅱ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为男性且车速超过的车辆数为，若每次抽取的结果是相互独立的，求 的分布列和数学期望． 参考公式与数据：，其中 ‎0.150‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎[来源:学科网ZXXK]‎ 附件1：律师事务所反盗版维权声明 附件2：独家资源交换签约学校名录（放大查看）‎ 学校名录参见：http://www.zxxk.com/wxt/list.aspx?ClassID=3060 ‎