广东省佛山市2020届高三教学质量检测数学理试题
2019~2020学年佛山市普通高中高三教学质量检测(二)
数学(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
注意事项:
1.答卷前,考生要务必填写答题卷上的有关项目.
2.选择题每小题选出答案后,用2B铅笔把答案涂在答题卷相应的位置上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改
动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效.
4.请考生保持答题卷的整洁.考试结束后,将答题卷交回.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|x2>2 x },B={x|1≤x≤3},则A∪B=( )
A、{x|0≤x<1} B、{x|x<0或x³1}
C、{x|2<x≤3} D、{x|x≤1或x>3}
2.复数z满足(z+2)(1+i)=3+i,则|z|=()
A、1 B、 C、 D、2
3.(1-)10的二项展开式中,x的系数与x4的系数之差为( )
A、-220 B、-90 C、90 D、0
4.设变量x,y满足约束条件,则目标函数z=x+6y的最大值为()
A、3 B、4 C、18 D、40
5.设函数=(sinx+cosx)2+cos2x,则下列结论错误的是()
A、的最小正周期为π B、y=的图像关于直线x=对称
C、的最大值为+1 D、的一个零点为x=
6.已知,则()
A、a
0)的准线上,过点A的直线与抛物线在第一象限相切于点B,记抛物线的焦点为F,则|BF|=()
A、6 B、8 C、10 D、12
8.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为()
A、 B、 C、 D、
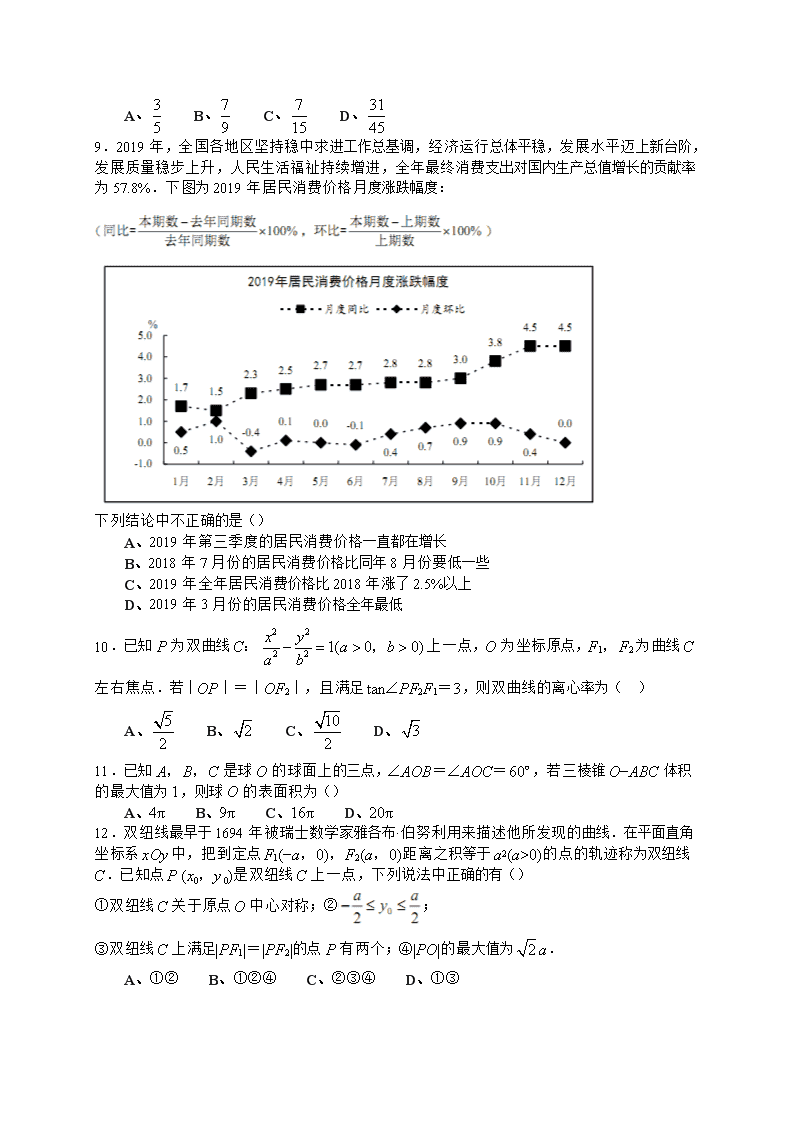
9.2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:
下列结论中不正确的是()
A、2019年第三季度的居民消费价格一直都在增长
B、2018年7月份的居民消费价格比同年8月份要低一些
C、2019年全年居民消费价格比2018年涨了2.5%以上
D、2019年3月份的居民消费价格全年最低
10.已知P为双曲线C:上一点,O为坐标原点,F1,F2为曲线C左右焦点.若|OP|=|OF2|,且满足tanÐPF2F1=3,则双曲线的离心率为( )
A、 B、 C、 D、
11.已知A,B,C是球O的球面上的三点,ÐAOB=ÐAOC=60º,若三棱锥O-ABC体积的最大值为1,则球O的表面积为()
A、4π B、9π C、16π D、20π
12.双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系xOy中,把到定点F1(-a,0),F2(a,0)距离之积等于a2(a>0)的点的轨迹称为双纽线C.已知点P (x0,y 0)是双纽线C上一点,下列说法中正确的有()
①双纽线C关于原点O中心对称;②;
③双纽线C上满足|PF1|=|PF2|的点P有两个;④|PO|的最大值为a.
A、①② B、①②④ C、②③④ D、①③
第Ⅱ卷(非选择题共90分)
本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~23为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分,满分20分.
13.设命题,则Øp为 .
14.已知函数,若f (a)=-3,则f(-a)= .
15.在面积为1的平行四边形ABCD中,ÐDAB=,则=________;
点P是直线AD上的动点,则的最小值为________.
16.数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).
该小组在操场上选定A点,此时测量视线和铅锤线之间的夹角在量角器上度数为37º;推动自行车直线后退,轮子滚动了10圈达到B点,此时测量视线和铅锤线之间的夹角在量角器上度数为53o.测量者站立时的“眼高”为1.55m,根据以上数据可计算得该建筑物的高度约为 米.(精确到0.1)
参考数据:
三、解答题:本大题共7小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知等比数列{an}的前n项和为Sn(Sn¹0),满足S1,S2,-S3成等差数列,且a1a2=a3.
(1)求数列{an}的通项公式;
(2)设,求数列{bn}的前n项和Tn.
18.(本小题满分12分)
如图,在四棱锥PABCD-中,底面ABCD是矩形,PA=PD=,PB=PC=,
ÐAPB=ÐCPD=90o,点M,N分别是棱BC,PD的中点.
(1)求证:MN//平面PAB;
(2)若平面PAB^平面PCD,求直线MN与平面PCD所成角的正弦值.
19.(本小题满分12分)
已知椭圆C:的离心率为,且过点(2,1).
(1)求椭圆C的方程;
(2)过坐标原点的直线与椭圆交于MN,两点,过点M作圆x2+y2=2的一条切线,交椭圆于另一点P,连接PN,证明:|PM||=PN|.
20.(本小题满分12分)
2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x(5££x20)(件)与相应的生产总成本y(万元)的四组对照数据.
x
5
7
9
11
y
200
298
431
609
工厂研究人员建立了y与x的两种回归模型,利用计算机算得近似结果如下:
模型①:;
模型②:.
其中模型①的残差(实际值-预报值)图如图所示:
(1)根据残差分析,判断哪一个更适宜作为y关于x的回归方程?并说明理由;
(2)市场前景风云变幻,研究人员统计历年的销售数据得到每件
产品的销售价格q(万元)是一个与产量x相关的随机变量,分布列为:
结合你对(1)的判断,当产量x为何值时,月利润的预报期望值最大?最大值是多少(精确到0.1)?
21.(本小题满分12分)
已知函数-sinx (x³a).
(1)若0恒成立,求a的取值范围;
(2)若a<-,证明:在(0,)有唯一的极值点x0,
且.
请考生在第22,23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号.
22.(本小题满分10分)[选修44-:坐标系与参数方程选讲]
在平面直角坐标系xOy中,曲线C1的参数方程为为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为r=4cosq.
(1)说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(2)设点M的极坐标为(4,0),射线q=a(0
查看更多