安徽省利辛县阚疃金石中学2019-2020学年高二下学期线上教学评估检测（期中）数学试题

安徽省利辛县阚疃金石中学2019-2020学年高二下学期线上教学评估检测（期中）数学试题

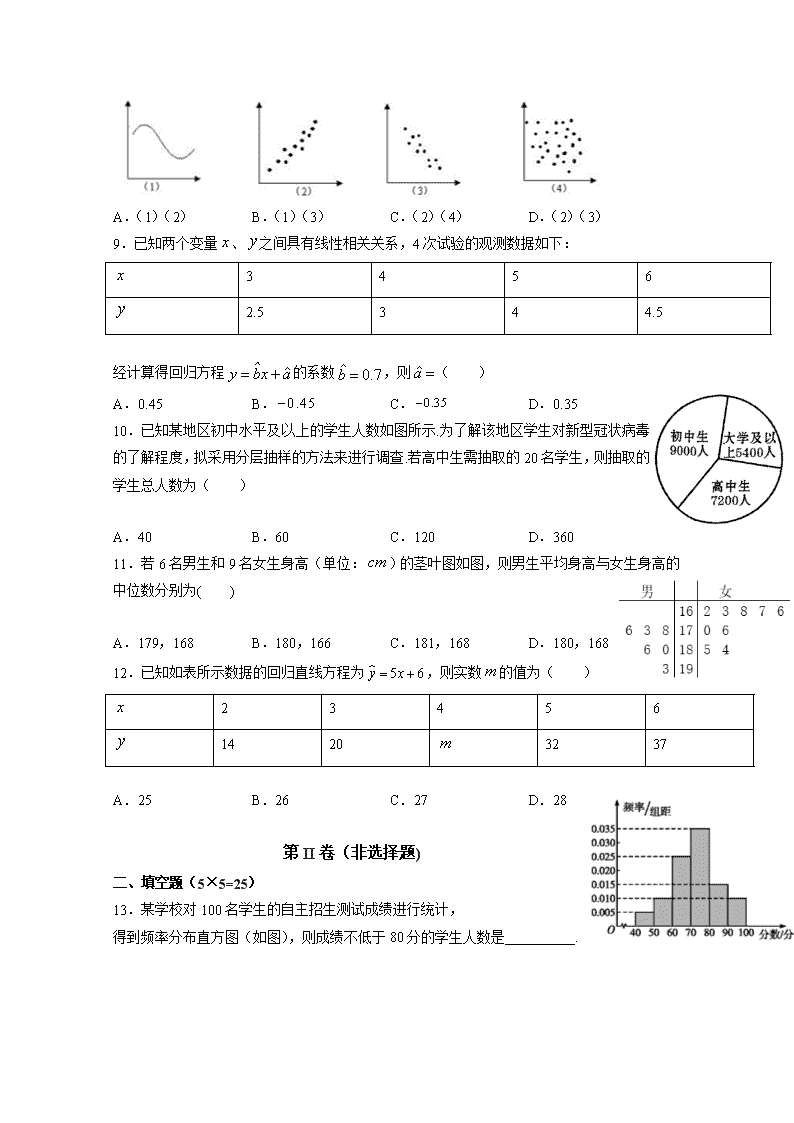
绝密★启用前 阚疃金石中学2020年春高二数学线上教学评估检测卷 考试时间：120分钟；满分：150；‎ 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 第I卷（选择题)‎ 一、单选题（5×12=60）‎ ‎1．某班45名同学都参加了立定跳远和100米跑两项体育学业水平测试，立定跳远和100米跑合格的人数分别为30和35，两项都不合格的人数为5.现从这45名同学中按测试是否合格分层（分成两项都合格、仅立定跳远合格、仅100米跑合格、两项都不合格四种）抽出9人进行复测，那么抽出来复测的同学中两项都合格的有（ ）‎ A．1人 B．2人 C．5人 D．6人 ‎2．一公司共有750名职工，其中青年职工350人，中年职工250人，老年职工150人，用分层抽样的方法从中抽取样本.若样本中的青年职工为14人，则样本容量为（ ）‎ A．15 B．25 C．30 D．35‎ ‎3．关于简单随机抽样,下列说法正确的是( )‎ ‎①它要求被抽取样本的总体的个数有限;②它是从总体中逐个地进行抽取;③不做特殊说明时它是一种不放回抽样;④它是一种等可能性抽样 A．①②③④ B．③④ C．①②③ D．①③④‎ ‎4．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是（ ）‎ A．消耗1升汽油，乙车最多可行驶5千米 B．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多 C．甲车以80千米/小时的速度行驶1小时，消耗8升汽油 D．某城市机动车最高限速80千米/小时.相同条件下，在该市用乙车比用丙车更省油 ‎5．甲、乙两工人在同样的条件下生产，日产量相等，每天出废品的情况如下表所列：‎ 工人 ‎ 甲 ‎ 乙 ‎ 废品数 ‎ ‎0 ‎ ‎1 ‎ ‎2 ‎ ‎3 ‎ ‎0 ‎ ‎1 ‎ ‎2 ‎ ‎3 ‎ 概率 ‎ ‎0.4 ‎ ‎0.3 ‎ ‎0.2 ‎ ‎0.1 ‎ ‎0.3 ‎ ‎0.5 ‎ ‎0.2 ‎ ‎0 ‎ 则有结论（　　）‎ A．甲的产品质量比乙的产品质量好一些 B．乙的产品质量比甲的产品质量好一些 C．两人的产品质量一样好 D．无法判断谁的质量好一些 ‎6．党的十八大以来，脱贫工作取得巨大成效，全国农村贫困人口大幅减少.如图的统计图反映了2012﹣2019年我国农村贫困人口和农村贫困发生率的变化情况（注：贫困发生率＝贫困人数（人）÷统计人数（人）×100%）.根据统计图提供的信息，下列推断不正确的是（ ）‎ A．2012﹣2019年，全国农村贫困人口逐年递减 B．2013﹣2019年，全国农村贫困发生率较上年下降最多的是2013年 C．2012﹣2019年，全国农村贫困人口数累计减少9348万 D．2019年，全国各省份的农村贫困发生率都不可能超过0.6%‎ ‎7．统计某校名学生的某次数学同步练习成绩（满分150分），根据成绩分数分成六组：，，，，，，绘制频率分布直方图如图所示，若已知不低于140分的人数为110，则的值是（ ）‎ A．800 B．900‎ C．1200 D．1000‎ ‎8．在下列各图中，每个图的两个变量具有线性相关关系的图是（ ）‎ ‎ ‎ A．（1）（2） B．（1）（3） C．（2）（4） D．（2）（3）‎ ‎9．已知两个变量、之间具有线性相关关系，4次试验的观测数据如下：‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ 经计算得回归方程的系数，则（ ）‎ A．0.45 B． C． D．0.35‎ ‎10．已知某地区初中水平及以上的学生人数如图所示.为了解该地区学生对新型冠状病毒的了解程度，拟采用分层抽样的方法来进行调查.若高中生需抽取的20名学生，则抽取的学生总人数为（ ）‎ A．40 B．60 C．120 D．360‎ ‎11．若6名男生和9名女生身高（单位：）的茎叶图如图，则男生平均身高与女生身高的中位数分别为( )‎ A．179，168 B．180，166 C．181，168 D．180，168‎ ‎12．已知如表所示数据的回归直线方程为，则实数的值为（ ）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎14‎ ‎20‎ ‎32‎ ‎37‎ A．25 B．26 C．27 D．28‎ 第II卷（非选择题)‎ 二、填空题（5×5=25）‎ ‎13．某学校对100名学生的自主招生测试成绩进行统计，‎ 得到频率分布直方图（如图），则成绩不低于80分的学生人数是__________.‎ ‎14．对某种电子元件使用寿命跟踪调查，所得样本频率分布直方图如图，若一批电子元件中寿命在100~300小时的电子元件的数量为400，则寿命在500~600小时的电子元件的数量为_______.‎ ‎15．已知一组数据，，，，的方差为2，则数据，，，，的方差为______.‎ ‎16．从某单位45名职工中随机抽取6名职工参加一项社区服务活动，用随机数法确定这6名职工.选取方法是先将45名职工编号，分别为01，02，03，…，45，然后从下面的随机数表第一行的第5列的数字7开始由左到右依次选取两个数字，从而确定6个个体的编号，则选出的第6个职工的编号为______________.‎ ‎17．某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名．现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为______.‎ 三、解答题（第18、20、21、23题各10分，第19题12分，第22题13分，共65分）‎ ‎18．某校高三（1）班在一次语文测试结束后，发现同学们在背诵内容方面失分较为严重.为了提升背诵效果，班主任倡议大家在早、晚读时间站起来大声诵读，为了解同学们对站起来大声诵读的态度，对全班50名同学进行调查，将调查结果进行整理后制成下表：‎ 考试分数 频数 ‎5‎ ‎10‎ ‎15‎ ‎5‎ ‎10‎ ‎5‎ 赞成人数 ‎4‎ ‎6‎ ‎9‎ ‎3‎ ‎6‎ ‎4‎ ‎（1）欲使测试优秀率为30%，则优秀分数线应定为多少分？‎ ‎（2）依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系，列出2×2列联表，并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.‎ 参考公式及数据：，.‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎19．某贫困地区共有1500户居民，其中平原地区1050户，山区450户.为调查该地区2017年家庭收入情况，从而更好地实施“精准扶贫”，采用分层抽样的方法，收集了150户家庭2017年年收入的样本数据（单位：万元）.‎ ‎（1）应收集多少户山区家庭的样本数据？‎ ‎（2）根据这150个样本数据，得到2017年家庭收入的频率分布直方图（如图所示），其中样本数据分组区间为（0，0.5]，（0.5，1]，（1，1.5]，（1.5，2]，（2，2.5]，（2.5，3].如果将频率视为概率，估计该地区2017年家庭收入超过1.5万元的概率；‎ ‎（3）样本数据中，有5户山区家庭的年收入超过2万元，请完成2017年家庭收入与地区的列联表，并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”？‎ 超过2万元 不超过2万元 总计 平原地区 山区 ‎5‎ 总计 附：‎ P（K2≥k0）‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎20．从甲、乙两种玉米苗中各抽10株，分别测得它们株高如下（单位：）：‎ 问：（1）哪种玉米的苗长得高？‎ ‎（2）哪种玉米的苗长得整齐？‎ ‎21．甲、乙两人在相同条件下各射击次，每次中靶环数情况如图所示：‎ ‎（1）请填写下表（先写出计算过程再填表）：‎ 平均数 方差 命中环及环以上的次数 甲 乙 ‎（2）从下列三个不同的角度对这次测试结果进行分析：‎ ‎①从平均数和方差相结合看（分析谁的成绩更稳定）；‎ ‎②从平均数和命中环及环以上的次数相结合看（分析谁的成绩好些）；‎ ‎③从折线图上两人射击命中环数的走势看（分析谁更有潜力）.‎ ‎22．某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．‎ ‎（1）求直方图中的值；‎ ‎（2）求月平均用电量的众数和中位数；‎ ‎（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？‎ ‎23．某快递网点收取快递费用的标准是重量不超过的包裹收费10元，重量超过的包裹，除收费10元之外，超过的部分，每超出（不足，按计算）需要再收费5元．该公司近60天每天揽件数量的频率分布直方图如下图所示（同一组数据用该区间的中点值作代表）．‎ ‎（1）求这60天每天包裹数量的平均数和中位数；‎ ‎（2）该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润，剩余的作为其他费用．已知该网点有工作人员3人，每人每天工资100元，以样本估计总体，试估计该网点每天的利润有多少元？‎ 高二数学参考答案 一、选择题（5×12=60）‎ ‎1．C 2．C 3．A 4．C 5．B 6．D 7．D 8．D 9．D 10．B 11．C 12．C 二、填空题（5×5=25）‎ ‎13．‎ ‎14．300‎ ‎15．8‎ ‎16．35‎ ‎17．8‎ 三、简答题（第18、20、21、23题各10分，第19题12分，第22题13分，共65分）‎ ‎18．（1）125分（2）列联表见解析；没有90%的把握认为赞成与否的态度与成绩是否优秀有关系 ‎19．（1）45户（2）0.45（3）填表见解析；有90%的把握认为“该地区2017年家庭年收入与地区有关”.‎ ‎20．（1）乙种玉米的苗长得高（2）乙种玉米的苗长得更整齐 ‎21．（1）详见解析；（2）①甲成绩比乙稳定；②乙成绩比甲好些；③乙更有潜力.‎ ‎22．（1）；（2），；（3）．‎ ‎23．（1）平均数和中位数都为260件； （2）1000元．‎