高中数学 第二节 证明不等式的基本方法、数学归纳法证明不等式课件 新人教A版选修4-5
第二节 证明不等式的基本方法、数学归纳法证明不等式
1.
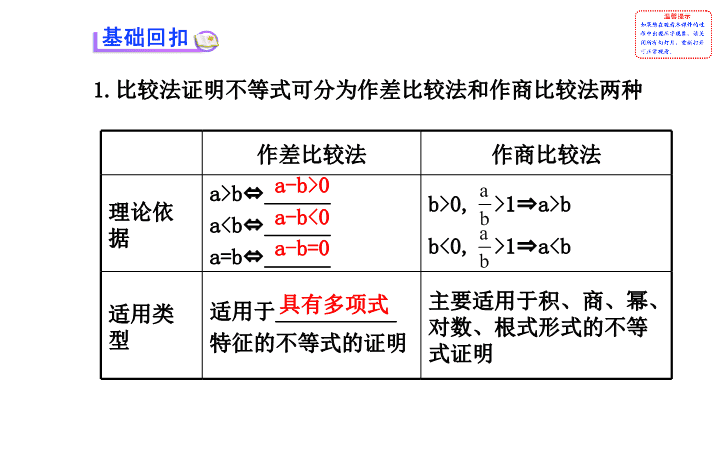
比较法证明不等式可分为作差比较法和作商比较法两种
作差比较法
作商比较法
理论依据
a>b
⇔
______
a
0, >1
⇒
a>b
b<0, >1
⇒
a0
a-b<0
a-b=0
具有多项式
2.
综合法和分析法
(1)
综合法
一般地,从
_________
出发,利用
_____
、公理、
_____
、性质
等,经过一系列的
_____
、
_____
而得出命题成立,这种证明
方法叫做综合法
.
综合法又叫
_________
或由因导果法
.
已知条件
定义
定理
推理
论证
顺推证法
(2)
分析法
证明命题时,从
___________
出发,逐步寻求使它成立的
_____
_____
,直至所需条件为
_________
或
___________________(
定
义、公理或已证明的定理、性质等
)
,从而得出要证的命题
成立,这种证明方法叫做分析法,这是一种执果索因的思考
和证明方法
.
要证的结论
已知条件
一个明显成立的事实
充分
条件
3.
反证法
(1)
假设要证的命题
_______
,以此为出发点,结合已知条件,
应用公理、定义、定理、性质等,进行正确的推理,得到和
___________(
或已证明的定理、性质、明显成立的事实等
)
矛盾
的结论,以说明假设不正确,从而证明
___________
,我们把它
称为反证法
.
(2)
证明步骤:反设→归谬→肯定原结论
.
不成立
命题的条件
原命题成立
4.
放缩法
(1)
证明不等式时,通过把不等式中的某些部分的值
_____
或
_____
,简化不等式,从而达到证明的目的,我们把这种方法
称为放缩法
.
(2)
理论依据
a
>
b,b
>
c
⇒
a___c.
放大
缩小
>
5.
数学归纳法
(1)
数学归纳法的概念
一般地,当要证明一个命题对于不小于某正整数
n
0
的所有正整
数
n
都成立时,可以用以下两个步骤:
①证明当
____
时命题成立;
②假设当
__________________
时命题成立,证明
______
时命题
也成立
.
在完成了这两个步骤后,就可以断定命题对于不小于
n
0
的所有
正整数都成立,这种证明方法称为数学归纳法
.
n=n
0
n=k(k∈N
+
,
且
k≥n
0
)
n=k+1
(2)
数学归纳法的基本过程
判断下面结论是否正确
(
请在括号中打“√”或“
×”).
(1)
若 则
x+2y>x-y.( )
(2)
已知
a>b>-1,
则
( )
(3)
设
(b>a>0)
,则
s≥t.( )
(4)
证明 可用比较法证明
.( )
(5)
数学归纳法的第一步
n
的初始值一定为
1.( )
【
解析
】
(1)
错误
.
若
x-y<0
,则有
x+2yb>-1,∴a+1>b+1>0,
(3)
错误
. ∵b>a>0,∴a-b<0,
a(a+1)>0,
(4)
错误
.
该不等式无论用作差法还是作商法都不好证明,最好
用分析法
.
(5)
错误
.
数学归纳法中的第一步
n
的初始值不一定为
1
,如证明
n
边形的内角和为
(n-2)
·
180°,
第
1
个值
n
0
=3.
答案:
(1)× (2)√ (3)× (4)× (5)×
考向
1
比较法证明不等式
【
典例
1】
(1)
设
c>b>a,
证明:
a
2
b+b
2
c+c
2
ab>a,∴b-a>0,c-b>0,c-a>0,
∴ab
2
+bc
2
+ca
2
>a
2
b+b
2
c+c
2
a,
即
a
2
b+b
2
c+c
2
a0,y>0,
求证
【
思路点拨
】
(1)
分析不等式左边的特点结合已知条件,利用基本不等式及重要不等式的变形证明该不等式
.
(2)
待证不等式中含有分数指数幂,不易直接证明
,
可考虑用分析法证明
.
两边六次方,消去分数指数幂,化为整式不等式后,再进行变形,整理证明即可
.
【
规范解答
】
(1)
方法一:左边
=a
2
+b
2
+4+
=4+a
2
+b
2
+
=4+a
2
+b
2
+1+
=4+(a
2
+b
2
)+2+
≥4+
当且仅当
a=b
时,等号成立
.
即原不等式成立
.
方法二:∵
a
,
b∈R
+
,且
a+b=1,∴ab≤
当且仅当
a=b
时,等号成立
.
∴(a+ )
2
+(b+ )
2
=4+(a
2
+b
2
)+
=4+
[
(a+b)
2
-2ab
]
+
(2)
要证明
只需证
(x
2
+y
2
)
3
>(x
3
+y
3
)
2
,
即证
x
6
+3x
4
y
2
+3x
2
y
4
+y
6
>x
6
+2x
3
y
3
+y
6
,
即证
3x
4
y
2
+3x
2
y
4
>2x
3
y
3
,
∵x>0,y>0,∴x
2
y
2
>0.
即证
3x
2
+3y
2
>2xy,∵3x
2
+3y
2
>x
2
+y
2
≥2xy,
∴3x
2
+3y
2
>2xy
成立,∴
【
拓展提升
】
1.
综合法证明不等式的方法
(1)
综合法证明不等式,要着力分析已知与求证之间,不等式的左右两端之间的差异与联系
.
合理进行转换,恰当选择已知不等式,这是证明的关键
.
(2)
在用综合法证明不等式时,不等式的性质和基本不等式是最常用的
.
在运用这些性质时,要注意性质成立的前提条件
.
2.
综合法与分析法的逻辑关系
用综合法证明不等式是
“
由因导果
”
,
分析法证明不等式是
“
执果索因
”
,它们是两种思路截然相反的证明方法
.
综合法往往是分析法的逆过程,表述简单、条理、清楚,所以在实际应用时,往往用分析法找思路,用综合法写步骤,由此可见
,
分析法与综合法相互转化,互相渗透,互为前提,充分利用这一辩证关系,可以增加解题思路,开阔视野
.
3.
分析法的应用
当所证明的不等式不能使用比较法,且和重要不等式、基本不等式没有直接联系,较难发现条件和结论之间的关系时,可用分析法来寻找证明途径,使用分析法证明的关键是推理的每一步必须可逆
.
【
变式训练
】
1.
已知
a,b∈R
+
,
且
a+b=1,
求证:
【
证明
】
方法一:∵
a
,
b∈(0
,
+∞)
,且
a+b=1,
∴ab≤
当且仅当
a=b
时,等号成立
.
方法二:
1-ab≥
当且仅当
a=b
时,等号成立
.
∴(1-ab)
2
≥ ∴(1-ab)
2
+1≥
又
方法三:
2.
已知
a>0,b>0,2c>a+b,
求证:
【
证明
】
要证:
只需证:
只需证:
|a-c|<
只需证:
(a-c)
2
a
2
+ab.
∵a>0,∴
只需证
2c>a+b,
由题设,上式显然成立
.
故
考向
3
用反证法或放缩法证明不等式
【
典例
3】
若
a
3
+b
3
=2
,求证
:a+b≤2.
【
思路点拨
】
直接证明
a+b≤2
比较困难,可考虑从反面入手,
运用反证法,导出矛盾,从而证得结论
.
【
规范解答
】
方法一
:
假设
a+b
>
2,
而
a
2
-ab+b
2
但取等号的条件为
a=b=0,
显然不可能
,
∴a
2
-ab+b
2
>
0.
则
a
3
+b
3
=(a+b)(a
2
-ab+b
2
)
>
2(a
2
-ab+b
2
),
而
a
3
+b
3
=2,
故
a
2
-ab+b
2
<
1.
∴1+ab
>
a
2
+b
2
≥2ab.
从而
ab
<
1.
∴a
2
+b
2
<
1+ab
<
2.
∴(a+b)
2
=a
2
+b
2
+2ab
<
2+2ab
<
4.
∴a+b
<
2.
这与假设矛盾,故
a+b≤2.
方法二
:
假设
a+b
>
2
,则
a
>
2-b,
故
2=a
3
+b
3
>
(2-b)
3
+b
3
,即
2
>
8-12b+6b
2
,
即
(b-1)
2
<
0
,这不可能,从而
a+b≤2.
方法三
:
假设
a+b
>
2,
则
(a+b)
3
=a
3
+b
3
+3ab(a+b)
>
8.
由
a
3
+b
3
=2,
得
3ab(a+b)
>
6.
故
ab(a+b)
>
2.
又
a
3
+b
3
=(a+b)(a
2
-ab+b
2
)=2,
∴ab(a+b)
>
(a+b)(a
2
-ab+b
2
),
∴a
2
-ab+b
2
<
ab,
即
(a-b)
2
<
0,
这不可能,故
a+b≤2.
【
拓展提升
】
1.
适宜用反证法证明的数学命题
(1)
结论本身是以否定形式出现的一类命题
.
(2)
关于唯一性、存在性的命题
.
(3)
结论以
“
至多
”“
至少
”
等形式出现的命题
.
(4)
结论的反面比原结论更具体、更容易研究的命题
.
2.
使用反证法证明问题时,准确地作出反设
(
即否定结论
)
,是正确运用反证法的前提,常见的
“
结论词
”
与
“
反设词
”
列表如下:
结论词
反设词
结论词
反设词
至少有一个
一个也没有
对所有
x
成立
存在某个
x
不成立
至多有一个
至少有两个
对任意
x
不成立
存在某个
x
成立
至少有
n
个
至多有
n-1
个
p
或
q
﹁
p
且
﹁
q
至多有
n
个
至少有
n+1
个
p
且
q
﹁
p
或
﹁
q
3.
放缩法证明不等式的技巧
放缩法证明不等式,就是利用不等式的传递性证明不等关系,即要证
a
>
b
,只需先证明
a
>
p
,且
p
>
b.
其中
p
的确定是最重要,也是最困难的,要凭借对题意的深刻分析,对式子巧妙变形的能力以及一定的解题经验
.
【
变式训练
】
若
n
是大于
1
的自然数
,
求证
:
【
证明
】
考向
4
数学归纳法的应用
【
典例
4】
已知
f(n)=
当
n>1,n∈N
时,求证:
f(2
n
)>
【
思路点拨
】
解答本题可先验证
n=2
时不等式成立,再假设
n=k
时不等式成立,推出
n=k+1
时不等式成立
.
【
规范解答
】
(1)
当
n=2
时,
f(2
2
)=
成立
.
(2)
假设当
n=k(k∈N
且
k≥2)
时不等式成立,
即
f(2
k
)=
成立
.
则当
n=k+1
时,
f(2
k+1
)=
即当
n=k+1
时不等式成立
.
由
(1)(2)
知,对于任意的
n>1,n∈N,
不等式成立
.
【
拓展提升
】
数学归纳法的应用
数学归纳法是用来证明与正整数
n
有关的数学命题的一种常用方法,应用时应注意以下三点:
(1)
验证是基础
数学归纳法的原理表明:第一个步骤是要找一个数
n
0
,这个
n
0
就是要证明的命题对象的最小正整数,这个正整数并不一定都是
“
1
”
,因此
“
找准起点,奠基要稳
”
是正确运用数学归纳法第一个要注意的问题
.
(2)
递推乃关键
数学归纳法的实质在于递推,所以从
“
k
”
到
“
k+1
”
的过程,必须把归纳假设
“
n=k
”
作为条件来导出
“
n=k+1
”
时的命题,在推导过程中,要把归纳假设用上一次或几次
.
(3)
寻找递推关系
①在第一步验证时,不妨多计算几次,并争取正确写出来,这样对发现递推关系是有帮助的
.
②
探求数列通项公式要善于观察式子的变化规律,观察
n
处在哪个位置
.
③
在书写
f(k+1)
时,一定要把包含
f(k)
的式子写出来,尤其是
f(k)
中的最后一项,除此之外,多了哪些项,少了哪些项要分清楚
.
【
变式训练
】
用数学归纳法证明:
n∈N
+
时,
【
证明
】
(1)
当
n=1
时,左边
=
等式成立
.
(2)
假设
n=k
时, 成立
.
当
n=k+1
时,
所以
n=k+1
时,等式成立
.
根据
(1)(2)
可得对一切
n∈N
+
,
等式均成立
.