- 2021-06-11 发布 |
- 37.5 KB |
- 44页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2015年数学理高考课件7-4 直线、平面平行的判定及其性质
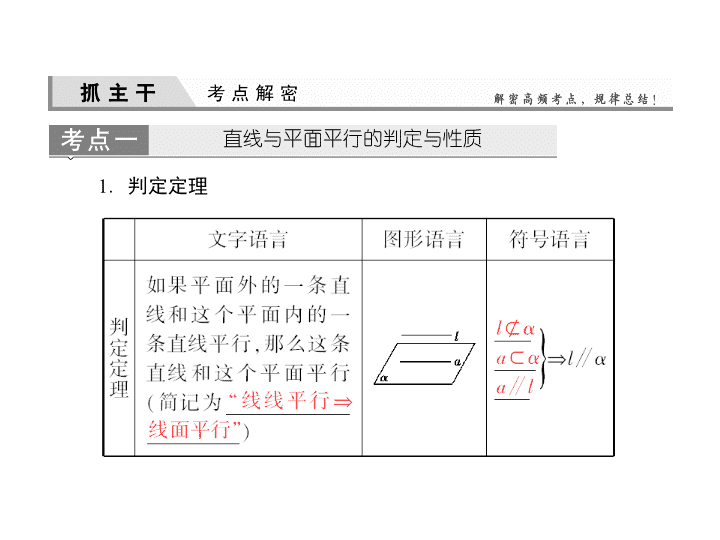
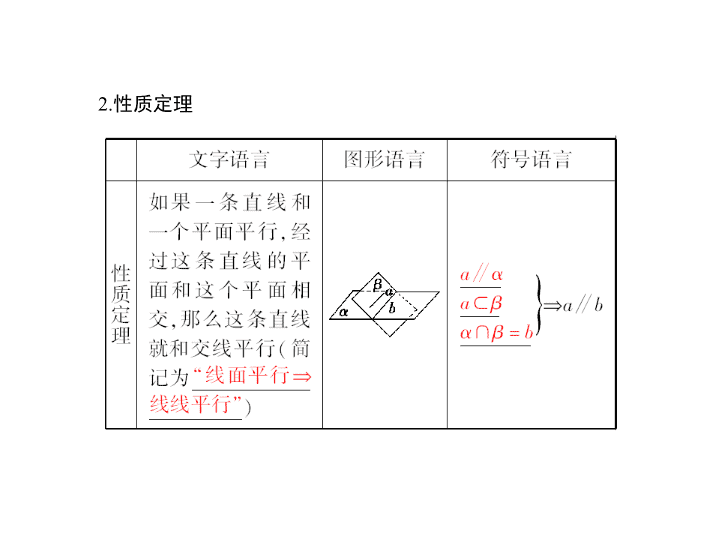
[ 最新考纲展示 ] 1 . 以立体几何的有关定义、公理和定理为出发点,认识和理解空间中线面平行、面面平行的有关性质与判定定理,并能够证明相关性质定理. 2. 能运用公理、定理和已获得的结论证明一些空间图形的平行关系的简单命题. 第四节 直线、平面平行的判定及其性质 直线与平面平行的判定与性质 1 . 判定定理 2. 性质定理 1 .设 m , l 表示直线, α 表示平面,若 m ⊂ α ,则 l ∥ α 是 l ∥ m 的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 答案: D 答案: C 平面与平面平行的判定与性质 1 .判定定理 2. 两平面平行的性质定理 3. 平行关系的转化关系 ____________________[ 通关方略 ]____________________ 平面与平面平行的几个有用性质 (1) 两个平面平行,其中一个平面内的任意一条直线平行于另一个平面. (2) 夹在两个平行平面之间的平行线段长度相等. (3) 经过平面外一点有且只有一个平面与已知平面平行. (4) 两条直线被三个平行平面所截,截得的对应线段成比例. (5) 如果两个平面分别平行于第三个平面,那么这两个平面互相平行. (6) 如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行. 3 .下列条件中,能判断两个平面平行的是 ( ) A .一个平面内的一条直线平行于另一个平面 B .一个平面内的两条直线平行于另一个平面 C .一个平面内有无数条直线平行于另一个平面 D .一个平面内任何一条直线都平行于另一个平面 解析: 由面面平行的定义可知选 D. 答案: D 4 .已知平面 α ∥ β ,直线 a ⊂ α ,有下列说法: ① a 与 β 内的所有直线平行; ② a 与 β 内无数条直线平行; ③ a 与 β 内的任意一条直线都不垂直. 其中真命题的序号是 ________ . 解析: 由面面平行的性质可知,过 a 与 β 相交的平面与 β 的交线才与 a 平行,故 ① 错误; ② 正确;平面 β 内的直线与直线 a 平行,异面均可,其中包括异面垂直,故 ③ 错误. 答案: ② 平行关系基本问题 【 例 1】 (1)(2013 年高考广东卷 ) 设 l 为直线, α , β 是两个不同的平面.下面命题中正确的是 ( ) A .若 l ∥ α , l ∥ β ,则 α ∥ β B .若 l ⊥ α , l ⊥ β ,则 α ∥ β C .若 l ⊥ α , l ∥ β ,则 α ∥ β D .若 α ⊥ β , l ∥ α ,则 l ∥ β (2) (2014 年潍坊模拟 ) 已知 m 、 n 、 l 1 、 l 2 表示直线, α , β 表示平面.若 m ⊂ α , n ⊂ α , l 1 ⊂ β , l 2 ⊂ β , l 1 ∩ l 2 = M ,则 α ∥ β 的一个充分条件是 ( ) A . m ∥ β 且 l 1 ∥ α B . m ∥ β 且 n ∥ β C . m ∥ β 且 n ∥ l 2 D . m ∥ l 1 且 n ∥ l 2 [ 解析 ] (1) 对于命题 A , α 和 β 可能平行也可能相交. ∴ A 错误;对于命题 B , α ∥ β 正确, ∴ B 正确;对于命题 C ,若 l ⊥ α , l ∥ β ,则 α ⊥ β , ∴ C 错误;对于命题 D , l ⊥ β , l ∥ β , l ⊂ β 均有可能,故 D 错. (2) 由定理 “ 如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行 ” 可得,由选项 D 可推知 α ∥ β ,因此选 D. [ 答案 ] (1)B (2)D 反思总结 解决有关线面平行,面面平行的判定与性质的基本问题要注意 (1) 注意判定定理与性质定理中易忽视的条件,如线面平行的条件中线在面外易忽视. (2) 结合题意构造或绘制图形,结合图形作出判断. (3) 会举反例或用反证法推断命题是否正确. 变式训练 1 . (2014 年江西盟校联考 ) 设 l 表示直线, α 、 β 表示平面.给出四个结论: ① 如果 l ∥ α ,则 α 内有无数条直线与 l 平行; ② 如果 l ∥ α ,则 α 内任意的直线与 l 平行; ③ 如果 α ∥ β ,则 α 内任意的直线与 β 平行; ④ 如果 α ∥ β ,对于 α 内的一条确定的直线 a ,在 β 内仅有唯一的直线与 a 平行. 以上四个结论中,正确结论的个数为 ( ) A . 0 B . 1 C . 2 D . 3 解析: 本题考查了立体几何中平行的判定和性质.若 l ∥ α ,则在 α 内的直线与 l 平行或异面,故 ① 正确, ② 错误.由面面平行的性质知 ③ 正确.对于 ④ ,在 β 内有无数条直线与 a 平行,故 ④ 错误.故选 C. 答案: C 直线与平面平行的判定与性质 【 例 2】 (2013 年高考福建卷 ) 如图,在四棱锥 P - ABCD 中, PD ⊥ 平面 ABCD , AB ∥ DC , AB ⊥ AD , BC = 5 , DC = 3 , AD = 4 , ∠ PAD = 60°. [ 解析 ] (1) 在梯形 ABCD 中,过点 C 作 CE ⊥ AB ,垂足为 E . 由已知得,四边形 ADCE 为矩形, AE = CD = 3 ,在 Rt △ BEC 中,由 BC = 5 , CE = 4 ,依勾股定理得 BE = 3 ,从而 AB = 6. 又由 PD ⊥ 平面 ABCD 得, PD ⊥ AD , 正视图如图所示: 证法二 取 AB 的中点 E ,连接 ME , DE . 在梯形 ABCD 中, BE ∥ CD ,且 BE = CD , ∴ 四边形 BCDE 为平行四边形, ∴ DE ∥ BC ,又 DE ⊄ 平面 PBC , BC ⊂ 平面 PBC , ∴ DE ∥ 平面 PBC . 又在 △ PAB 中, ME ∥ PB , ME ⊄ 平面 PBC , PB ⊂ 平面 PBC , ∴ ME ∥ 平面 PBC ,又 DE ∩ ME = E , ∴ 平面 DME ∥ 平面 PBC . 又 DM ⊂ 平面 DME , ∴ DM ∥ 平面 PBC . 反思总结 证明直线与平面平行,一般有以下几种方法 (1) 若用定义直接判定,一般用反证法; (2) 用判定定理来证明,关键是在平面内找 ( 或作 ) 一条直线与已知直线平行,证明时注意用符号语言叙述证明过程; (3) 应用两平面平行的一个性质,即两平面平行时,其中一个平面内的任何直线都平行于另一个平面. 平面与平面平行的判定与性质 [ 解析 ] (1) 证明:由题设知, BB 1 綊 DD 1 , ∴ BB 1 D 1 D 是平行四边形, ∴ BD ∥ B 1 D 1 . 又 BD ⃘ 平面 CD 1 B 1 , ∴ BD ∥ 平面 CD 1 B 1 . ∵ A 1 D 1 綊 B 1 C 1 綊 BC , ∴ A 1 BCD 1 是平行四边形, ∴ A 1 B ∥ D 1 C . 又 A 1 B ⃘ 平面 CD 1 B 1 , ∴ A 1 B ∥ 平面 CD 1 B 1 . 又 ∵ BD ∩ A 1 B = B , ∴ 平面 A 1 BD ∥ 平面 CD 1 B 1 . 反思总结 判定平面与平面平行的方法 (1) 利用定义; (2) 利用面面平行的判定定理; (3) 利用面面平行的判定定理的推论; (4) 面面平行的传递性 ( α ∥ β , β ∥ γ ⇒ α ∥ γ ) ; (5) 利用线面垂直的性质 ( l ⊥ α , l ⊥ β ⇒ α ∥ β ). —— 立体几何中的探索性问题 解决探究性问题一般要采用执果索因的方法,假设求解的结果存在,从这个结果出发,寻找使这个结论成立的充分条件,如果找到了符合题目结果要求的条件,则存在;如果找不到符合题目结果要求的条件 ( 出现矛盾 ) ,则不存在.常见的类型有: (1) 条件探索型 (2) 结论探索性. 条件探索型 ∴ BC 綊 EF . ∴ 四边形 BCEF 是平行四边形. ∴ CE ∥ BF . 又 ∵ BF ⊂ 平面 SAB , CE ⊄ 平面 SAB , ∴ CE ∥ 平面 SAB . 由题悟道 条件探索型问题一般先依据条件猜测位置,然后给出证明,从线段上探索点多为中点或三等分点的某一点. 结论探索型 (1) 求证: BD ⊥ PC ; (2) 求证: MN ∥ 平面 PDC ; (3) 设平面 PAB ∩ 平面 PCD = l ,试问直线 l 是否与直线 CD 平行,请说明理由. [ 解析 ] (1) 证明:因为 △ ABC 是正三角形, M 是 AC 的中点,所以 BM ⊥ AC ,即 BD ⊥ AC . 又因为 PA ⊥ 面 ABCD , BD ⊂ 面 ABCD ,所以 PA ⊥ BD , 又 PA ∩ AC = A ,所以 BD ⊥ 面 PAC , 又 PC ⊂ 面 PAC ,所以 BD ⊥ PC . 由题悟道 结论探索型问题多用直接推证或间接推证即利用反证法. 如图所示,在长方体 ABCD - A 1 B 1 C 1 D 1 中, E 、 F 、 G 、 H 分别是棱 CC 1 、 C 1 D 1 、 D 1 D 、 DC 的中点, N 是 BC 的中点,点 M 在四边形 EFGH 及其内部运动,则 M 满足条件 ________ 时,有 MN ∥ 平面 B 1 BDD 1 . 解析: 连接 FH , HN , FN ,由题意知 HN ∥ 面 B 1 BDD 1 , FH ∥ 面 B 1 BDD 1 ,且 FH ∩ HN = H , ∴ 面 NHF ∥ 面 B 1 BDD 1 , ∴ 当 M 在线段 HF 上运动时,有 MN ∥ 面 B 1 BDD 1 . 答案: M ∈ 线段 HF 本小节结束 请按 ESC 键返回查看更多