- 2021-06-11 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2019届天津市武清区高二上学期期中考试(2017-11)
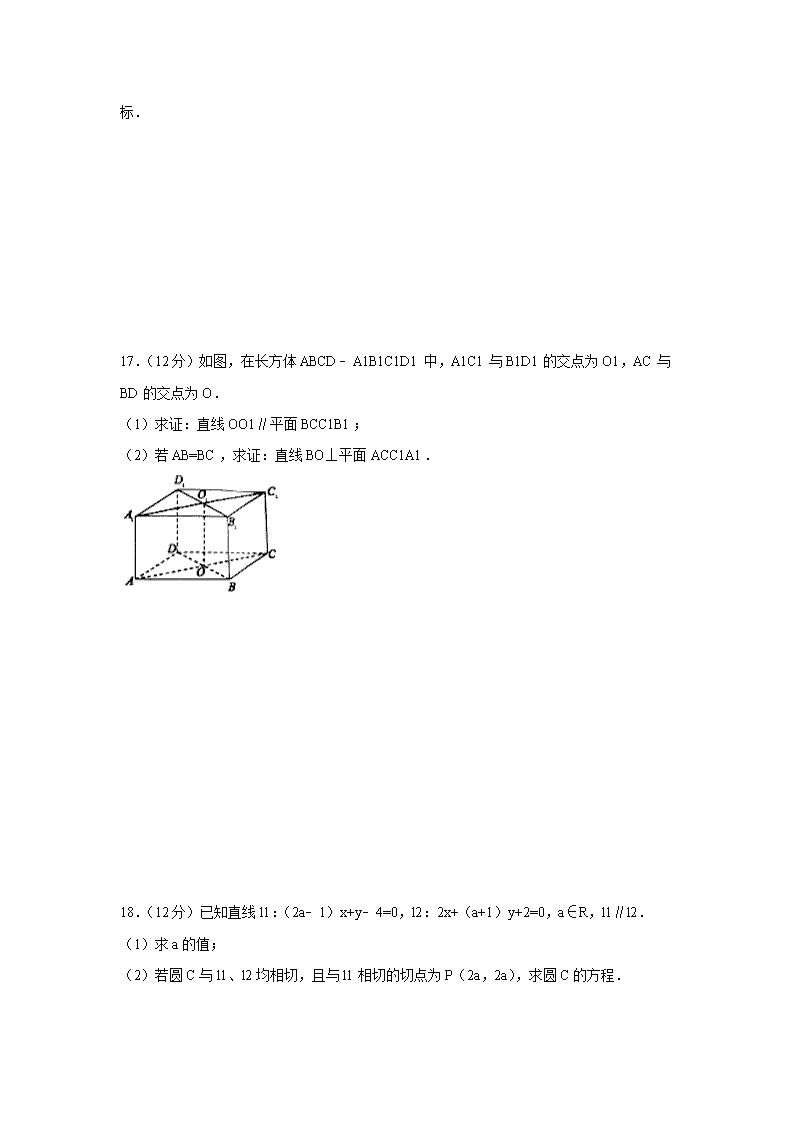
2017-2018学年天津市武清区高二(上)期中数学试卷(理科) 一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1.直线x+y﹣1=0的倾斜角是( ) A. B. C. D. 2.用“斜二测”画法画出△ABC(A为坐标原点,AB在x轴上)的直观图为△A′B′C′,则△A′B′C′的面积与△ABC的面积的比为( ) A. B. C. D. 3.过三点A(﹣3,2),B(3,﹣6),C(0,3)的圆的方程为( ) A.x2+y2+4y﹣21=0 B.x2+y2﹣4y﹣21=0 C.x2+y2+4y﹣96=0 D.x2+y2﹣4y﹣96=0 4.直线(3a+1)x+2y﹣4=0与直线2x+2ay﹣1=0垂直,则实数a的值为( ) A.﹣1 B.﹣1或 C.﹣ D. 5.已知正方体ABCD﹣A1B1C1D1的棱长为1,以A为坐标原点,向量,,的方向分别为x,y,z轴的正方向建立空间直角坐标系Axyz,则点C1的坐标为( ) A.(1,1,1) B.(﹣1,﹣1,1) C.(1,﹣1,﹣1) D.(1,﹣1,1) 6.直线3x+4y﹣10=0与圆x2+y2﹣2x+6y+2=0的位置关系是( ) A.相交且直线经过圆心 B.相交但直线不经过圆心 C.相切 D.相离 7.已知m、n、l是不同的直线,α、β是不同的平面,则下列说法中不正确的是( ) ①m⊂α,l∩α=A,点A∉m,则l与m不共面; ②l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α; ③若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β; ④若l∥α,m∥β,α∥β,则l∥m. A.① B.② C.③ D.④ 8.已知圆C1:f(x,y)=0,圆C2:g(x,y)=0,若存在两点A(x1,y1),B(x2,y2)满足f(x1,y1)<0,f(x2,y2)>0,g(x1,y1)<0,g(x2,y2)<0,则C1与C2的位置关系为( ) A.相交 B.相离 C.相交或C1在C2内 D.相交或C2在C1内 9.如图是一棱锥的三视图,在该棱锥的侧面中,面积最大的侧面的面积为( ) A.4 B. C.2 D. 10.直线l1,l2分别过点A(3,2),B(,6),它们分别绕点A,B旋转,但始终保持l1⊥l2.若l1与l2的交点为P,坐标原点为O,则线段OP长度的取值范围是( ) A.[3,9] B.[3,6] C.[6,9] D.[9,+∞) 二、填空题:本大题共5小题,每小题4分,共20分). 11.与点P(3,﹣2)关于直线x﹣1=0对称的点的坐标是 . 12.棱长为2的四面体的体积为 . 13.直线的斜率为k,若﹣1<k<,则直线的倾斜角的范围是 . 14.球的内接圆柱的底面积为4π,侧面积为12π,则该球的体积为 . 15.过点P(3,1)作直线l将圆C:x2+y2﹣4x﹣5=0分成两部分,当这两部分面积之差最小时,直线l的方程是 . 三、解答题:本大题共5小题,共60分.解答写出文字说明、证明过程或演算过程. 16.(12分)已知三点A(1,2),B(﹣3,0),C(3,﹣2). (1)求证△ABC为等腰直角三角形; (2)若直线3x﹣y=0上存在一点P,使得△PAC面积与△ PAB面积相等,求点P的坐标. 17.(12分)如图,在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1,AC与BD的交点为O. (1)求证:直线OO1∥平面BCC1B1; (2)若AB=BC,求证:直线BO⊥平面ACC1A1. 18.(12分)已知直线l1:(2a﹣1)x+y﹣4=0,l2:2x+(a+1)y+2=0,a∈R,l1∥l2. (1)求a的值; (2)若圆C与l1、l2均相切,且与l1相切的切点为P(2a,2a),求圆C的方程. 19.(12分)已知圆C:(x﹣1)2+(y﹣1)2=1上存在4个点到直线x+y﹣m=0(m∈R)的距离等于1﹣. (1)求m的取值范围; (2)判断圆C与圆D:x2+y2﹣2mx=0的位置关系. 20.(12分)如图,已知在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为CE的中点. (1)求直线AF与平面ACD所成的角; (2)求证:平面BCE⊥平面DCE. 2017-2018学年天津市武清区高二(上)期中数学试卷(理科) 参考答案 一、选择题: 1.B;2.C;3.A;4.C;5.D;6.D;7.D;8.C;9.B;10.A; 11. 12. 13. 14. 15. 16. (1)∵ ∴ ………………………3分 显然………………………4分 ∵,且 ………………………5分 ∴是以为顶点的等腰直角三角形…………………6分 (2)直线的方程为,即………………7分 直线的方程为,即………………8分 ∵点在直线上,∴可设 ∵,的面积与面积相等,∴点到直线的距离与到直线距离相等 即,即………………10分 解得,,∴点的坐标为………………12分 17. (1)∵在长方体中,∥且 ∴四边形为平行四边形………………………2分 ∵四边形、四边形均为矩形,∴分别是的中点 ∴∥………………………4分 ∵平面,平面………………………5分 ∴直线∥平面………………………6分 (2)在长方体中,,是平面内的两条相交直线,∴平面………………………8分 ∵平面 ∴………………………9分 ∵ ∴四边形为正方形,∴……………………10分 ∵是平面内的两条相交直线……………………11分 ∴直线平面……………………12分 18. (1)∵∥,∴……………………2分 解得或……………………3分 当时,直线的方程为,直线的方程为, 满足∥……………………4分 当时,直线的方程为,直线的方程为, 与重合……………………5分 ∴所求的值为1……………………6分 (2)与的距离为为圆的直径……………………7分 ∴圆的半径为……………………8分 设圆的圆心坐标为,∵,直线的斜率为,所以直线 的斜率为1,∵ ∴,即 ……………………9分 ∵,∴, 解得或…………10分 当时圆心不在与之间,应舍去………11分 ∴圆的方程为……………………12分 19. (1)依题意可知,圆上点到直线的距离应大于………………2分 圆心到直线的距离为…………………3分 ∴…………………5分 解得…………………6分 (2)圆的圆心为,半径为…………………………7分 ∵ 圆心距,半径差的绝对值为,半径和为………9分 显然,……………………11分 ∴圆与圆相交……………………12分 20. (1)取的中点,连接 ∵为的中点,∴∥且…………………1分 ∵⊥平面,∴平面…………………2分 ∴就是直线与平面所成的角…………………3分 令,∵ ∴在直角中,…………………5分 ∴…………………6分 (2)设,∵⊥平面,∴在直角中, 在直角梯形中, ∴ 连接 ∵为的中点 ∴ 且 ∵ ∴ 且 ∴是二面角的平面角…………………9分 连接,∵⊥平面 ∴在直角中, 在中,∵,∴是斜边为的直角三角形 ∴,…………………11分 ∴平面平面…………………12分查看更多