数学（文）卷·2018届湖北省阳新县兴国高级中学高二5月月考（2017-05）

数学（文）卷·2018届湖北省阳新县兴国高级中学高二5月月考（2017-05）

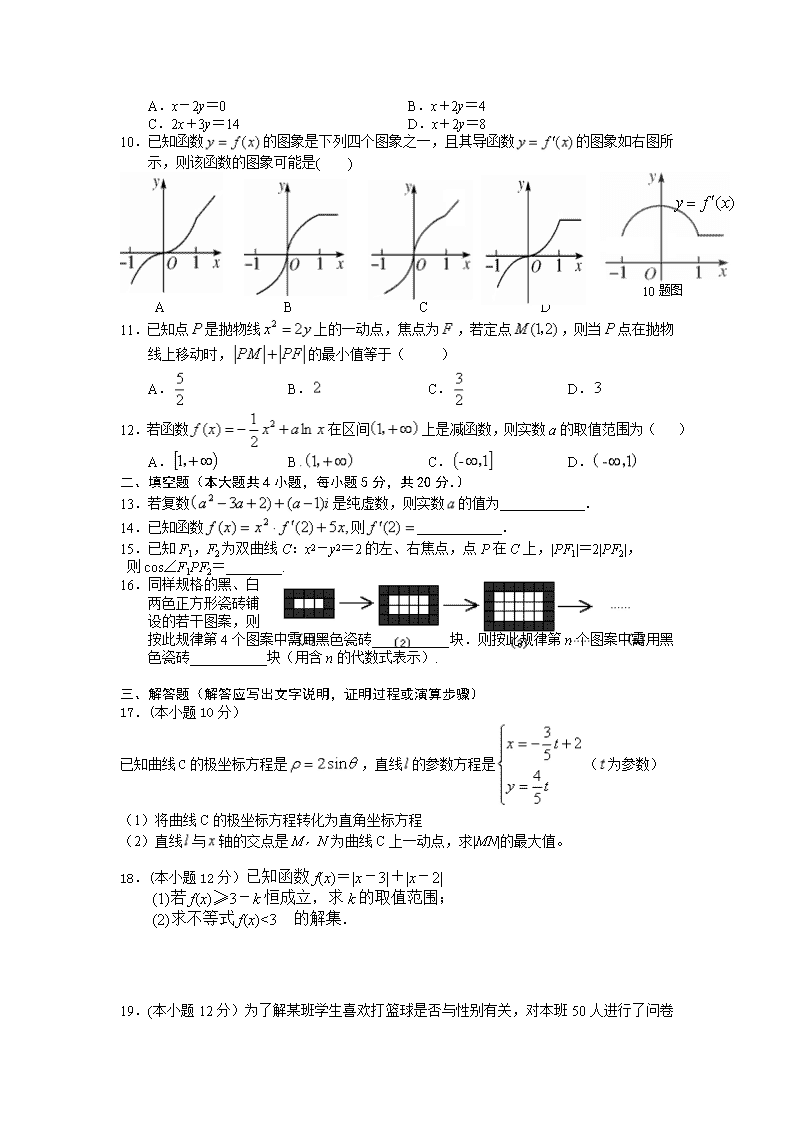
‎ 2017年兴国高中高二（文）5月月考 数学试题 命题人：李名来 审题人：伍坚 ‎ 一、选择题（本大题共12小题，每小题5分，共60分．）‎ ‎1．复数的共轭复数是（ ）‎ A． B． ‎ C． D． ‎ ‎2．若命题p：x＝2且y＝3，则¬ p为(　　)‎ A．x≠2或y≠3 B．x≠2且y≠3‎ C．x＝2或y≠3 D．x≠2或y＝3‎ ‎3．椭圆x2＋4y2＝1的离心率为(　　)‎ A. B． C. D． ‎4．用反证法证明命题：若整系数一元二次方程有有理数根，那么中至少有一个是偶数时，下列假设中正确的是（　 ）‎ A．假设都是偶数 B．假设都不是偶数 ‎ C．假设至多有一个偶数 D．假设至多有两个偶数 x ‎2‎ ‎3‎ ‎4‎ y ‎6‎ ‎4‎ ‎5‎ ‎5．已知x、y的取值如右表所示：如果与呈线性相关，且线性回归方程为，则（ ）‎ ‎ A． B． C． D．1‎ ‎6．变量X与Y相对应的一组数据为(10，1)，(11.3，2)，(11.8，3)，(12.5，4)，(13，5)；变量U与V相对应的一组数据为(10，5)，(11.3，4)，(11.8，3)，(12.5，2)，(13，1)，r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则(　　)‎ A．r2＜r1＜0 B．0＜r2＜r1 C．r2＜0＜r1 D．r2＝r1‎ ‎7．已知椭圆＋＝1的两个焦点为F1，F2，弦AB过点F1，则△ABF2的周长为(　　)‎ A．10 B．20‎ C．2 D．4 ‎8．已知，， ，…，若（a，t均为正实数）．类比以上等式，可推测a，t的值，则t＋a＝（ ）．‎ A．41 B．42 C．39 D．38‎ ‎9．椭圆＋＝1的弦被点(4,2)平分，则此弦所在的直线方程是(　　)‎ A．x－2y＝0 B．x＋2y＝4‎ C．2x＋3y＝14 D．x＋2y＝8‎ ‎10．已知函数的图象是下列四个图象之一，且其导函数的图象如右图所示，则该函数的图象可能是( )‎ ‎10题图 ‎ A B C D ‎ ‎11．已知点是抛物线上的一动点，焦点为，若定点，则当点在抛物线上移动时，的最小值等于（ ） ‎ A． B． C． D．‎ ‎12．若函数在区间上是减函数，则实数a的取值范围为（ ）‎ A． B C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13．若复数是纯虚数，则实数的值为 ．‎ ‎14．已知函数则 ．‎ ‎15．已知F1，F2为双曲线C：x2－y2＝2的左、右焦点，点P在C上，|PF1|＝2|PF2|，‎ 则cos∠F1PF2＝________.‎ ‎16．同样规格的黑、白 两色正方形瓷砖铺 设的若干图案，则 按此规律第4个图案中需用黑色瓷砖___________块．则按此规律第n个图案中需用黑色瓷砖___________块（用含n的代数式表示）.‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤）‎ ‎17．(本小题10分）‎ 已知曲线C的极坐标方程是，直线的参数方程是（为参数）‎ （1） 将曲线C的极坐标方程转化为直角坐标方程 ‎（2）直线与轴的交点是M，N为曲线C上一动点，求|MN|的最大值。‎ ‎18．(本小题12分）已知函数f(x)＝|x－3|＋|x－2|‎ ‎(1)若f(x)≥3－k恒成立，求k的取值范围；‎ ‎(2)求不等式f(x)<3 的解集．‎ ‎19．(本小题12分）为了解某班学生喜欢打篮球是否与性别有关，对本班50人进行了问卷调查，得到如下的列联表：‎ 喜欢打篮球 不喜欢打篮球 合计 男生 ‎5‎ 女生 ‎10‎ 合计 ‎50‎ 已知在全部50人中随机抽取1人抽到喜欢打篮球的学生的概率为.‎ ‎⑴请将上面的列联表补充完整(不用写计算过程)；（请将答案填写在答题卡中的列联表上）‎ ‎⑵能否在犯错误的概率不超过0.005的前提下认为喜欢打篮球与性别有关?请说明你的理由；参考公式及数据：，其中n＝a＋b＋c＋d ‎ P(K2≥kn)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ kn ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎20．（本小题12分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y(吨标准煤)的几组对照数据 x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎(1)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y＝bx＋a；‎ ‎(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?‎ ‎(参考数值3×2.5＋4×3＋5×4＋6×4.5＝66.5)‎ ‎（附：，，其中，为样本平均值）‎ ‎21．（本小题12分）‎ 在直角坐标系xOy中，点P到两点(0，－)，(0，)的距离之和等于4，‎ ‎(1)求点P的轨迹方程；‎ ‎(2) 设点P的轨迹为C，直线y＝kx＋1与C交于A，B两点，若⊥，求k的值．‎ ‎22．(本小题满分12分)已知函数f(x)＝xln x.‎ ‎(1)求f(x)的单调区间；‎ ‎(2)若对所有的x≥1都有f(x)≥ax－1，求实数a的取值范围．‎ ‎2017年兴国高中高二（文）5月数学试题（答案）‎ 一、选择题：‎ ‎1-5 BAABB 6-10 CDADC 11-12 AC 二、填空题：‎ ‎13. 2 14. 15. 16. 24；4(n＋2) ‎ 三、 解答题 ‎17.（1）.……5分 ‎ (2) .……10分 ‎18. (1)对任意x∈R恒成立，即(|x－3|＋|x－2|)min≥3－k. ‎ 又|x－3|＋|x－2|≥|x－3－x＋2|＝1，(|x－3|＋|x－2|)min＝1≥3－k，‎ 解得k≥2. .……6分 ‎(2) （1,4）.……12分 ‎19. (1)‎ 喜欢打篮球 不喜欢打篮球 合计 男生 ‎20‎ ‎5‎ ‎25‎ 女生 ‎10‎ ‎15‎ ‎25‎ 合计 ‎30‎ ‎20‎ ‎50‎ ‎ ………………5分 （2） ‎∵ …………10分 ‎∴在犯错误的概率不超过0.005的前提下认为喜欢打篮球与性别有关。…12分 ‎20．解： (1)由对照数据，计算得：＝86，‎ ＝＝4.5(吨)，‎ ＝＝3.5(吨)．‎ 已知＝66.5，所以，由最小二乘法确定的回归方程的系数为：‎ ‎＝＝＝0.7，‎ ‎＝－＝3.5－0.7×4.5＝0.35.‎ 因此，所求的线性回归方程为＝0.7x＋0.35 .……8分 ‎(2)由(1)的回归方程及技改前生产100吨甲产品的生产能耗，得降低的生产能耗为：‎ ‎90－(0.7×100＋0. 35)＝19.65(吨标准煤) ． ……12分 ‎21. 解析：　(1)设P(x，y)，由椭圆定义可知，点P的轨迹C是以(0，－)、(0，)为焦点，长半轴为2的椭圆，‎ 它的短半轴b＝＝1，‎ 故曲线C的方程为x2＋＝1. ………5分 ‎(2)设A(x1，y1)，B(x2，y2)，联立方程 消去y并整理得(k2＋4)x2＋2kx－3＝0.‎ 其中Δ＝4k2＋12(k2＋4)>0恒成立．‎ 故x1＋x2＝－，x1x2＝－. ………7分 若⊥，即x1x2＋y1y2＝0.‎ 而y1y2＝k2x1x2＋k(x1＋x2)＋1，‎ 于是x1x2＋y1y2＝－－－＋1＝0，‎ 化简得－4k2＋1＝0，‎ 所以k＝±. ………12分 ‎22解析：　(1)f(x)的定义域为(0，＋∞)，f′(x)＝1＋ln x，‎ 令f′(x)>0，解得x>，令f′(x)<0，解得01时，g′(x)>0，‎ ‎∴g(x)在[1，＋∞)上是增加的，‎ 所以g(x)的最小值为g(1)＝1.则a≤1.‎ 故a的取值范围是(－∞，1]． ………12分