高中数学选修2-2教学课件3_2_2 复数代数形式的乘除运算

高中数学选修2-2教学课件3_2_2 复数代数形式的乘除运算

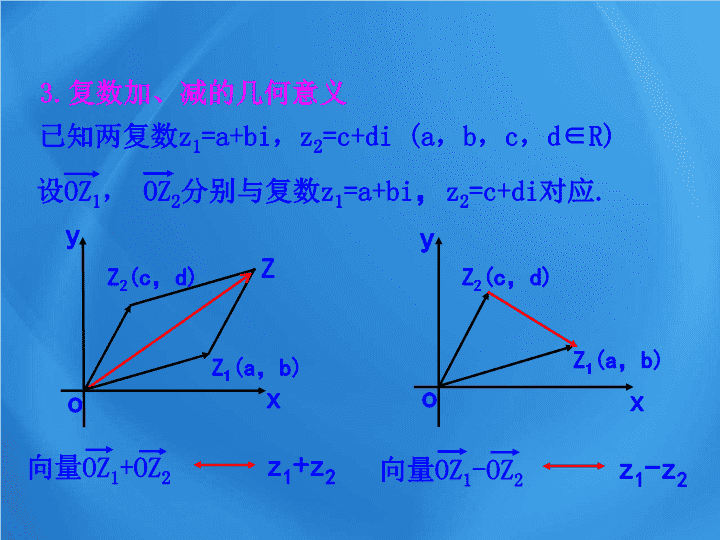
3.2.2 复数代数形式的乘除运算 已知两复数 z 1 =a+bi ， z 2 =c+di (a ， b ， c ， d∈R) (a+bi)±(c+di) =________________. 1. 加法、减法的运算法则 2. 加法运算律： 对任意 z 1 ， z 2 ， z 3 ∈C z 1 +z 2 =z 2 +z 1 , (z 1 +z 2 )+z 3 =z 1 +(z 2 +z 3 ) 交换律： 结合律： (a±c)+(b±d)i 已知两复数 z 1 =a+bi ， z 2 =c+di (a ， b ， c ， d∈R) 3. 复数加、减的几何意义 设 OZ 1 ， OZ 2 分别与复数 z 1 =a+bi ， z 2 =c+di 对应 . x o y Z 1 (a ， b) Z 2 (c ， d) Z o x y Z 2 (c ， d) Z 1 (a ， b) 向量 OZ 1 +OZ 2 z 1 +z 2 向量 OZ 1 -OZ 2 z 1 -z 2 复平面中点 Z 1 与点 Z 2 间的距离 |z 1 -z 2 | 表示： _________ ______________. 已知两复数 z 1 =a+bi ， z 2 =c+di (a ， b ， c ， d∈R) 4. 复数模的几何意义： Z 1 (a ， b) o x y Z 2 (c ， d) 特别地， |z| 表示： ______________________. 复平面中点 Z 与原点间的距 离 如： |z+(1+2i)| 表示： _________________ _______________. 点 (-1 ， -2) 的距离 点 Z( 对应复数 z) 到 掌握复数的代数形式的乘法与除法运算法则 . （重点） 2. 对复数除法法则的运用 . （难点） 3. 乘法的运算法则与运算律 . 4. 共轭复数的定义是什么 . 探究点 1 复数乘法运算 我们规定，复数乘法法则如下： 设 z 1 =a+bi,z 2 =c+di 是任意两个复数，那么它们的乘积为： ( a+bi )( c+di )= ac+adi+bci+bdi 2 = ac+adi+bci-bd = (ac-bd)+(ad+bc)i. 即 ( a+bi )( c+di )= (ac-bd)+(ad+bc)i 注意： 两个复数的积是一个确定的复数 . 探究点 2 复数乘法的运算律 复数的乘法是否满足交换律，结合律以及乘法对加法的分配律？ 请验证乘法是否满足交换律 ? 对任意复数 z 1 =a+bi,z 2 =c+di 则 z 1 ·z 2 =( a+bi )( c+di )=ac+adi+bci+bdi 2 =ac+adi+bci-bd =(ac-bd)+(ad+bc)i 而 z 2 ·z 1 = ( c+di )( a+bi )=ac+bci+adi+bdi 2 =(ac-bd)+(ad+bc)i 所以 z 1 · z 2 =z 2 · z 1 ( 交换律 ) 乘法运算律 对任意 z 1 ,z 2 ,z 3 ∈C, 有 z 1 ·z 2 =z 2 ·z 1 ( 交换律 ) (z 1 ·z 2 )·z 3 = z 1 ·(z 2 ·z 3 ) ( 结合律 ) z 1 (z 2 +z 3 )=z 1 ·z 2 +z 1 ·z 3 ( 分配律 ) 例 1 计算 (1-2i)(3+4i)(-2+i). 解 : (1-2i)(3+4i)(-2+i) =(11-2i)(-2+i) =-20+15i. 分析： 类似两个多项式相乘，把 i 2 换成 -1 例 2 计算 :(1) (3+4i)(3-4i); (2) (1+i) 2 . 解 : (1)(3+4i)(3-4i) =3 2 -(4i) 2 =9-(-16) =25. (2)(1+i) 2 =1+2i+i 2 =1+2i-1 =2i. 【 总结提升 】 （ 1 ）实数集中的乘法公式在复数集中仍然成立； （ 2 ）复数的混合运算也是先乘方，再乘除，最后加减，有括号应先处理括号里面的． 探究点 3 共轭复数的定义 　　 一般地，当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为 共轭复数 . 虚部不等于０的两个共轭复数也叫做 共轭虚数 . 实数 的共轭复数是它本身 . 思考 ：若 z 1 ， z 2 是共轭复数，那么 　　（１）在复平面内，它们所对应的点有怎样的位置关系？ 　　（２） z 1 ·z 2 是一个怎样的数？ 记法： 复数 z= a+b i 的共轭复数记作 = a-b i 解： ⑴作图 y x (a,b) (a,-b) z 1 =a+b i o y x (a,0) z 1 =a o x y z 1 =b i (0,b) (0,-b) o 得出结论： 在复平面内，共轭复数 z 1 ,z 2 所对应的点关于 实轴 对称 . ⑵ 令 z 1 =a+b i, 则 z 2 =a-b i 则 z 1 ·z 2 =(a+b i )(a-b i ) =a 2 -ab i +ab i -b 2 i 2 =a 2 +b 2 结论： 任意两个互为共轭复数的乘积是一个实数 . 探究点 4 共轭复数 的相关运算性质   探究点 5 复数除法的法则 类比实数的除法是乘法的逆运算，我们规定复数的除法是乘法的逆运算 . 试探求复数除法的法则 . 复数除法的法则是 : 方法 : 在进行复数除法运算时 , 通常先把 在作根式除法时 , 分子分母都乘以分母的“有理化因式” , 从而使分母“有理化” . 这里分子分母都乘以分母的“实数化因式” ( 共轭复数 ), 从而使分母“实数化” . 先写成分式形式 然后分母实数化 , 分子分母同时乘以分母的共轭复数 结果化简成代数形式 B 2. 若复数 z=1+i (i 为虚数单位 ) 是 z 的共轭复数 ， 则 + 的虚部为（ ） A. 0 B. -1 C. 1 D. -2 3. （ 2014 ·新课标全国 卷 Ⅱ ） ( ) A ． B. C. D. B A 5. 已知方程 x 2 - 2 x +2=0 有两虚根为 x 1 , x 2 , 求 x 1 4 + x 2 4 的值 . 注 : 在复数范围内方程的根与系数的关系仍适用 . i i 1. 复数相乘类似于多项式相乘，只要在所得的结果中把 i 2 换成－ 1 ，并且把实部和虚部分别合并 . 2. 实数系中的乘法公式在复数系中仍然成立 . 3. 当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为 共轭复数 . 虚部不等于０的两个共轭复数也叫做 共轭虚数 . 实数 的共轭复数是它本身 . 4. 复数代数形式的除法实质：分母实数化 . 男儿不展风云志，空负天生八尺躯 .