2019届二轮复习(理)2-5-3-2空间中的垂直与空间角课件（25张）

2019届二轮复习(理)2-5-3-2空间中的垂直与空间角课件（25张）

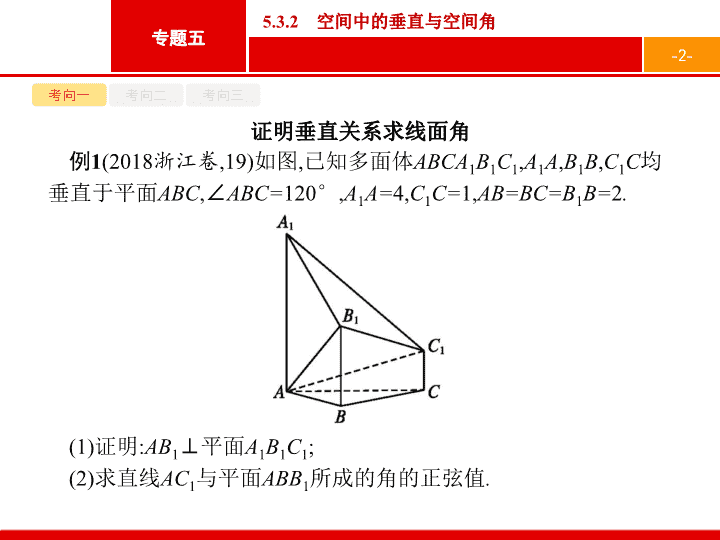
5.3.2 　空间中的垂直与空间角 - 2 - 考向一 考向二 考向三 证明垂直关系求线面角 例 1 (2018 浙江卷 ,19) 如图 , 已知多面体 ABCA 1 B 1 C 1 , A 1 A , B 1 B , C 1 C 均垂直于平面 ABC , ∠ ABC= 120 ° , A 1 A= 4, C 1 C= 1, AB=BC=B 1 B= 2 . ( 1) 证明 : AB 1 ⊥ 平面 A 1 B 1 C 1 ; (2) 求直线 AC 1 与平面 ABB 1 所成的角的正弦值 . - 3 - 考向一 考向二 考向三 - 4 - 考向一 考向二 考向三 - 5 - 考向一 考向二 考向三 - 6 - 考向一 考向二 考向三 解题心得 求线面角可以用几何法 , 即 “ 先找 , 后证 , 再求 ”, 也可以通过平面的法向量来求 , 即求出斜线的方向向量与平面的法向量所夹的锐角 , 取其余角就是斜线和平面所成的角 . - 7 - 考向一 考向二 考向三 对点训练 1 (2018 全国卷 2, 理 20) 如图 , 在三棱锥 P-ABC 中 , AB=BC= 2 , PA=PB=PC=AC= 4, O 为 AC 的中点 . (1) 证明 : PO ⊥ 平面 ABC ; (2) 若点 M 在棱 BC 上 , 且二面角 M-PA-C 为 30 ° , 求 PC 与平面 PAM 所成角的正弦值 . - 8 - 考向一 考向二 考向三 - 9 - 考向一 考向二 考向三 - 10 - 考向一 考向二 考向三 - 11 - 考向一 考向二 考向三 证明垂直关系求二面角 例 2 如图 , 在四棱锥 P-ABCD 中 , AB ∥ CD , 且 ∠ BAP= ∠ CDP= 90 ° . (1) 证明 : 平面 PAB ⊥ 平面 PAD ; (2) 若 PA=PD=AB=DC , ∠ APD= 90 ° , 求二面角 A-PB-C 的余弦值 . - 12 - 考向一 考向二 考向三 - 13 - 考向一 考向二 考向三 - 14 - 考向一 考向二 考向三 解题心得 用向量求二面角 , 由于在求平面法向量的坐标时 , 坐标的取值不同 , 导致平面法向量的方向相反 , 所以两个法向量的夹角与二面角相等或互补 , 所以根据图形判断所求二面角是锐角还是钝角 , 进而确定二面角余弦值的正负 . - 15 - 考向一 考向二 考向三 对点训练 2 (2018 全国卷 3, 理 19) 如图 , 边长为 2 的正方形 ABCD 所在的平面与半 圆弧 所在 平面垂直 , M 是 上 异于 C , D 的点 . ( 1) 证明 : 平面 AMD ⊥ 平面 BMC ; (2) 当三棱锥 M-ABC 体积最大时 , 求面 MAB 与面 MCD 所成二面角的正弦值 . - 16 - 考向一 考向二 考向三 解 : (1) 由题设知 , 平面 CMD ⊥ 平面 ABCD , 交线为 CD. 因为 BC ⊥ CD , BC ⊂ 平面 ABCD , 所以 BC ⊥ 平面 CMD , 故 BC ⊥ DM. 因为 M 为 上 异于 C , D 的点 , 且 DC 为直径 , 所以 DM ⊥ CM. 又 BC ∩ CM=C , 所以 DM ⊥ 平面 BMC. 而 DM ⊂ 平面 AMD , 故平面 AMD ⊥ 平面 BMC. - 17 - 考向一 考向二 考向三 - 18 - 考向一 考向二 考向三 折叠问题中的空间角 例 3 (2018 全国卷 1, 理 18) 如图 , 四边形 ABCD 为正方形 , E , F 分别为 AD , BC 的中点 , 以 DF 为折痕把 △ DFC 折起 , 使点 C 到达点 P 的位置 , 且 PF ⊥ BF . (1) 证明 : 平面 PEF ⊥ 平面 ABFD ; (2) 求 DP 与平面 ABFD 所成角的正弦值 . - 19 - 考向一 考向二 考向三 - 20 - 考向一 考向二 考向三 - 21 - 考向一 考向二 考向三 解题心得 平面图形翻折后成为空间图形 , 翻折后还在一个平面上的线线和线面的关系不发生变化 , 不在同一个平面上的可能发生变化 . 解决这类问题就是要根据这些变与不变 , 去研究翻折以后的空间图形中的线面关系和各类几何量的度量值 . - 22 - 考向一 考向二 考向三 对点训练 3 (2018 湖南郴州二模 , 理 19) 如图 , 在长方形 ABCD 中 , AB= 4, BC= 2, 现将 △ ACD 沿 AC 折起 , 使 D 折到 P 的位置且 P 在面 ABC 的射影 E 恰好在线段 AB 上 . (1) 证明 : AP ⊥ PB ; (2) 求锐二面角 B-PC-E 的余弦值 . - 23 - 考向一 考向二 考向三 (1) 证明 由题知 PE ⊥ 平面 ABC , 又 BC ⊂ 平面 ABC , ∴ PE ⊥ BC. ∵ AB ⊥ BC 且 AB ∩ PE=E , ∴ BC ⊥ 平面 PAB. ∵ AP ⊂ 平面 PAB , ∴ BC ⊥ AP. ∵ AP ⊥ CP 且 BC ∩ CP=C , ∴ AP ⊥ 平面 PBC. ∵ PB ⊂ 平面 PBC , ∴ AP ⊥ PB. - 24 - 考向一 考向二 考向三 - 25 - 考向一 考向二 考向三