2018届高三数学一轮复习: 第8章 第3节 圆的方程
第三节 圆的方程
[考纲传真] 1.掌握确定圆的几何要素,掌握圆的标准方程与一般方程.2.初步了解用代数方法处理几何问题的思想.
1.圆的定义及方程
定义
平面内与定点的距离等于定长的点的集合(轨迹)
标准方程
(x-a)2+(y-b)2=r2(r>0)
圆心(a,b),半径r
一般方程
x2+y2+Dx+Ey+F=0,(D2+E2-4F>0)
圆心,
半径
2.点与圆的位置关系
点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系:
(1)若M(x0,y0)在圆外,则(x0-a)2+(y0-b)2>r2.
(2)若M(x0,y0)在圆上,则(x0-a)2+(y0-b)2=r2.
(3)若M(x0,y0)在圆内,则(x0-a)2+(y0-b)2<r2.
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”).
(1)确定圆的几何要素是圆心与半径.( )
(2)方程(x+a)2+(y+b)2=t2(t∈R)表示圆心为(a,b),半径为t的一个圆.( )
(3)方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是A=C≠0,B=0,D2+E2-4AF>0.( )
(4)若点M(x0,y0)在圆x2+y2+Dx+Ey+F=0外,则x+y+Dx0+Ey0+F>0.( )
[解析] 由圆的定义及点与圆的位置关系,知(1)(3)(4)正确.
(2)中,当t≠0时,表示圆心为(-a,-b),半径为|t|的圆,不正确.
[答案] (1)√ (2)× (3)√ (4)√
2.(教材改编)方程x2+y2+ax+2ay+2a2+a-1=0表示圆,则a的取值范围是( )
A.a<-2或a> B.-<a<0
C.-2<a<0 D.-2<a<
D [由题意知a2+4a2-4(2a2+a-1)>0,
解得-2<a<.]
3.(2016·全国卷Ⅱ)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( )
A.- B.-
C. D.2
A [圆x2+y2-2x-8y+13=0,得圆心坐标为(1,4),所以圆心到直线ax+y-1=0的距离d==1,解得a=-.]
4.(2017·西安质检)若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为________.
x2+(y-1)2=1 [两圆关于直线对称则圆心关于直线对称,半径相等,则圆C的圆心为(0,1),半径为1,标准方程为x2+(y-1)2=1.]
5.(2015·全国卷Ⅰ)一个圆经过椭圆+=1的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为________.
2+y2= [由题意知a=4,b=2,上、下顶点的坐标分别为(0,2),(0,-2),右顶点的坐标为(4,0).由圆心在x轴的正半轴上知圆过点(0,2),(0,-2),(4,0)三点.设圆的标准方程为(x-m)2+y2=r2(0
0),则解得所以圆的标准方程为2+y2=.]
求圆的方程
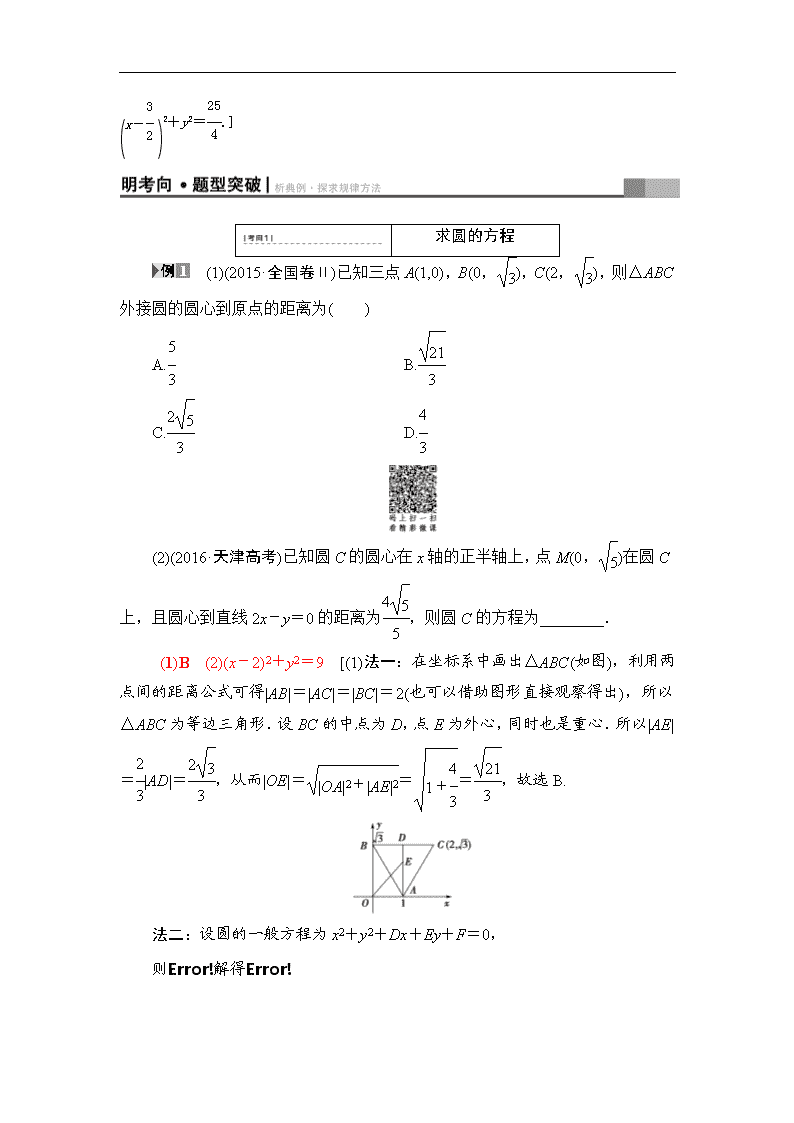
(1)(2015·全国卷Ⅱ)已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为( )
A. B.
C. D.
(2)(2016·天津高考)已知圆C的圆心在x轴的正半轴上,点M(0,)在圆C上,且圆心到直线2x-y=0的距离为,则圆C的方程为________.
(1)B (2)(x-2)2+y2=9 [(1)法一:在坐标系中画出△ABC(如图),利用两点间的距离公式可得|AB|=|AC|=|BC|=2(也可以借助图形直接观察得出),所以△ABC为等边三角形.设BC的中点为D,点E为外心,同时也是重心.所以|AE|=|AD|=,从而|OE|===,故选B.
法二:设圆的一般方程为x2+y2+Dx+Ey+F=0,
则解得
所以△ABC外接圆的圆心为.
因此圆心到原点的距离d==.
(2)因为圆C的圆心在x轴的正半轴上,设C(a,0),且a>0,
所以圆心到直线2x-y=0的距离d==,
解得a=2,
所以圆C的半径r=|CM|==3,
所以圆C的方程为(x-2)2+y2=9.]
[规律方法] 1.直接法求圆的方程,根据圆的几何性质,直接求出圆心坐标和半径,进而写出方程.
2.待定系数法求圆的方程:①若已知条件与圆心(a,b)和半径r有关,则设圆的标准方程,依据已知条件列出关于a,b,r的方程组,从而求出a,b,r的值;②若已知条件没有明确给出圆心或半径,则选择圆的一般方程,依据已知条件列出关于D,E,F的方程组,进而求出D,E,F的值.
温馨提醒:解答圆的方程问题,应注意数形结合,充分运用圆的几何性质.
[变式训练1] (2017·河南百校联盟联考)经过点A(5,2),B(3,-2),且圆心在直线2x-y-3=0上的圆的方程为________.
x2+y2-4x-2y-5=0(或(x-2)2+(y-1)2=10) [法一 ∵圆过A(5,2),B(3,-2)两点,
∴圆心一定在线段AB的垂直平分线上.
易知线段AB的垂直平分线方程为y=-(x-4).
设所求圆的圆心为C(a,b),则有
解得a=2,且b=1.
因此圆心坐标C(2,1),半径r=|AC|=.
故所求圆的方程为(x-2)2+(y-1)2=10.
法二 设圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
则
解得D=-4,E=-2,F=-5,
∴所求圆的方程为x2+y2-4x-2y-5=0.]
与圆有关的最值问题
已知M(x,y)为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)求的最大值和最小值.
[解] (1)由圆C:x2+y2-4x-14y+45=0,
可得(x-2)2+(y-7)2=8,
∴圆心C的坐标为(2,7),半径r=2.2分
又|QC|==4,
∴|MQ|max=4+2=6,
|MQ|min=4-2=2.5分
(2)可知表示直线MQ的斜率k.6分
设直线MQ的方程为y-3=k(x+2),即kx-y+2k+3=0.8分
由直线MQ与圆C有交点,所以≤2,
可得2-≤k≤2+,
∴的最大值为2+,最小值为2-.12分
[迁移探究1] (变化结论)在本例的条件下,求y-x的最大值和最小值.
[解] 设y-x=b,则x-y+b=0.3分
当直线y=x+b与圆C相切时,截距b取到最值,
∴=2,∴b=9或b=1.10分
因此y-x的最大值为9,最小值为1.12分
[迁移探究2] (变换条件结论)若本例中条件“点Q(-2,3)”改为“点Q是直线3x+4y+1=0上的动点”,其它条件不变,试求|MQ|的最小值.
[解] ∵圆心C(2,7)到直线3x+4y+1=0上动点Q的最小值为点C到直线3x+4y+1=0的距离,
∴|QC|min=d==7.5分
又圆C的半径r=2,
∴|MQ|的最小值为7-2.12分
[规律方法]
1.处理与圆有关的最值问题,应充分考虑圆的几何性质,并根据代数式的几何意义,数形结合求解.
2.某些与圆相关的最值可利用函数关系求最值.
根据题目条件列出关于所求目标式子的函数关系式,然后根据关系式的特征选用参数法、配方法、函数的性质、利用基本不等式求最值是比较常用的.
[变式训练2] 设P为直线3x-4y+11=0上的动点,过点P作圆C:x2+y2-2x-2y+1=0的两条切线,切点分别为A,B,求四边形PACB的面积的最小值.
[解] 圆的标准方程为(x-1)2+(y-1)2=1,2分
圆心为C(1,1),半径为r=1.5分
根据对称性可知,四边形PACB的面积为
2S△APC=2×|PA|r=|PA|=.8分
要使四边形PACB的面积最小,则只需|PC|最小,最小时为圆心到直线l:3x-4y+11=0的距离
d===2.10分
所以四边形PACB面积的最小值为
==.12分
与圆有关的轨迹问题
(2014·全国卷Ⅰ)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
[解] (1)圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.2分
设M(x,y),则=(x,y-4),=(2-x,2-y).
由题设知·=0,故x(2-x)+(y-4)(2-y)=0,
即(x-1)2+(y-3)2=2.
由于点P在圆C的内部,
所以M的轨迹方程是(x-1)2+(y-3)2=2.5分
(2)由(1)可知M的轨迹是以点N(1,3)为圆心,为半径的圆.
由于|OP|=|OM|,故O在线段PM的垂直平分线上.
又P在圆N上,从而ON⊥PM.7分
因为ON的斜率为3,所以l的斜率为-,
故l的方程为y=-x+.10分
又|OM|=|OP|=2,O到l的距离为,|PM|=,所以△POM的面积为.12分
[规律方法] 求与圆有关的轨迹问题的四种方法
(1)直接法:直接根据题设给定的条件列出方程求解.
(2)定义法:根据圆的定义列方程求解.
(3)几何法:利用圆的几何性质得出方程求解.
(4)代入法(相关点法):找出要求的点与已知点的关系,代入已知点满足的关系式求解.
[变式训练3] 已知点A(-1,0),点B(2,0),动点C满足|AC|=|AB|,求点C与点P(1,4)所连线段的中点M的轨迹方程.
【导学号:01772293】
[解] 由题意可知:动点C的轨迹是以(-1,0)为圆心,3为半径长的圆,方程为(x+1)2+y2=9.3分
设M(x0,y0),则由中点坐标公式可求得
C(2x0-1,2y0-4),6分
代入点C的轨迹方程得4x+4(y0-2)2=9,
化简得x+(y0-2)2=,10分
故点M的轨迹方程为x2+(y-2)2=.12分
[思想与方法]
1.确定一个圆的方程,需要三个独立条件,“选形式、定参数”是求圆的方程的基本方法.
2.解答圆的问题,应注意数形结合,充分运用圆的几何性质,简化运算.
[易错与防范]
1.二元二次方程x2+y2+Dx+Ey+F=0表示圆时易忽视D2+E2-4F>0这一前提条件.
2.求圆的方程需要三个独立条件,所以不论是设哪一种圆的方程都要列出系数的三个独立方程.
3.求轨迹方程和求轨迹是有区别的,求轨迹方程得出方程即可,而求轨迹在得出方程后还要指明轨迹表示什么曲线.